Пример (уравнение Эйлера).

Уравнение Эйлера (уравнение нелинейных волн).

(сравните с уравнением линейных волн:).

Воспользуемся теоремой 1. Выпишем характеристическую систему:

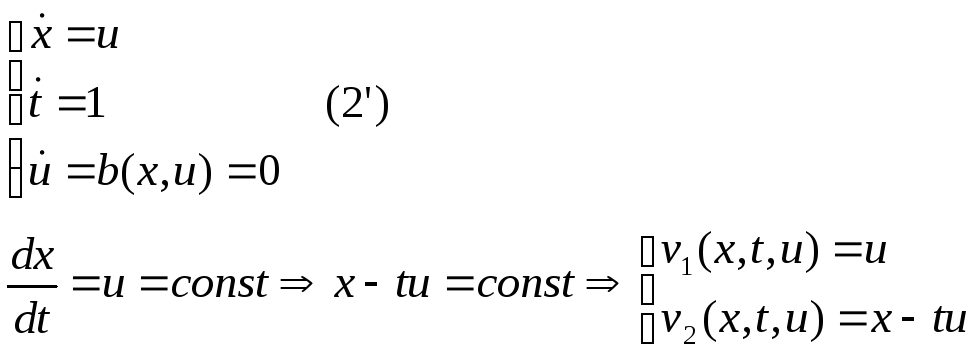
Ответ: u неявно задается соотношением:F(u,x-tu)=0  u=f(x-tu) (т.к.).

Замечание 2 (задача «гибдд»).

Уравнение нелинейных волн может быть получено при решении задачи «ГИБДД», а именно: рассмотрим модель однородной среды, состоящей из континуального множества точек, каждая из которых имеет начальную скорость v₀()и движется вдоль оси равномерно и прямолинейно (к примеру, это может быть жидкость).

- скорость потока.

( ,t) – в гидромеханикепеременные Лагранжа, а(x,t)–переменные Эйлера.

Определим скорость потока u.

U(X( ,t),t)=

Если тоx=X( ,t) имеет единственное решение = (x) 

Уравнение описывает поле скоростей.

Если здесь мы заменим  на автомобиль, то получим задачу «ГИБДД». Поле скоростей в потоке автомобилей удовлетворяет уравнению Эйлера.

Еслиu(x,t) станет многозначной функцией отx, то это значит, что в этой точке находится несколько частиц с разными скоростямивозникнет пробка, катастрофа. При этом условие (*) будет нарушено:

§3. Задача Коши для квазилинейного уравнения Постановка задачи Коши для квазилинейного уравнения.

Пусть n=2. Тогда квазилинейное уравнение принимает вид:

Пусть  - гладкая кривая вR²:

 ={x, x=X( )=(X₁( ),X₂( )),  I₀  R¹}.

Пусть u₀ – заданная функция на :

Задача {(1), (2)} – это задача Коши для квазилинейного уравнения(1).

Геометрическая интерпретация задачи в расширенном фазовом пространстве.

u(x₁,x₂)  S_u={(x,u)R³, u=u(x₁,x₂)}.

Назовем эту поверхность интегральной. Тогда решить задачу {(1), (2)} означает провести интегральную поверхность, взаимно однозначно проектируемую на конфигурационное пространство и проходящую через кривую (  ).

, гдеa(x,u)R²,-векторное полехарактеристической системы.

Перепишем соотношение (1) в эквивалентном векторном виде:

Здесь - нормаль.

Т.о. интегральная поверхность в каждой точке касается векторного поля характеристической системы (сравни с О.Д.У.).

А с другой стороны характеристика L_M={x=X( ), u=U( )} также касается векторного поля характеристической системыхарактеристика лежит на интегральной поверхности, или, другими словами, интегральная поверхность расслаивается на характеристики.

Задача.

Пусть M₀S_u.Доказать, что.

Мораль: как решать задачу Коши?

Надо взять начальные точки M₀, лежащие на кривойи из каждой точки выпустить характеристики. Их будет континуальное количество. И т.о. :

Алгоритм решения задачи Коши {(1), (2)}.

1)Выведем по виду уравнения (1) систему характеристик:

2) Поставим для этой системы задачу Коши с начальными условиями на кривой (см. рис.1) :

3)Решим систему {(1), (2)}, т.е. найдем семейство характеристикL_ , ( I₀) системы (1):

- поверхность в пространстве.

4) Разрешим систему {(3), (4)} относительно и :

При этом мы предполагаем, что выполнено условие

Формула работает только в области {x, x=X( , ),  I_ ,  I₀}=V_ ( ) --окрестность кривой .

5) Определим функциюu по формуле:

.

Утверждение 1 (о справедливости алгоритма).

Если функция u(x) определяется формулой (6), иu(x)C¹(V_ ( )), то она есть решение задачи Коши {(1), (2)}, причем единственное.

Доказательство.

1)Покажем, что

(5) 

Тогда

2)Надо доказать, что

Фиксируем точку MS_u. Через эту точку проходит единственная характеристикаL_ . Все такие характеристики не пересекаются.

Заметим, что:

Согласно алгоритму:

Т.к. M – произвольная точка, то (1’) выполнено в каждой точке окрестности.

Замечание (задача Коши для линейного уравнения).

Рассмотрим задачу Коши для общего линейного уравнения:

Алгоритм решения задачи Коши для системы {(7), (8)} получается из предыдущего алгоритма следующей заменой:

1)- характеристическая система в.

, т.к. здесьb(x,u)=f(x)-b(x)u.

2)

(9), (10) определяют систему характеристик l_ ={x=X( , ),  I_ , I₀ }.

Для (11) ставится задача Коши:

Решение задачи {(11), (12)} – решение однородного О.Д.У.

Пункты 3), 4), 5)следуют предыдущему алгоритму.

Утверждение, аналогичное утверждению 1, в данном случае доказывается в одну строчку в силу того, что

Заметим, что u(X( , ))=U( ,  )в силу (6).

Подставим равенство (13) в уравнение (11):

Т.о.  М имеет место уравнение (7).

§4. Корректность алгоритма решения задачи Коши

Теорема 1 (о корректности алгоритма для квазилинейного уравнения).

Пустьв областивыполнены следующие условия:

1)  иu₀ – гладкие функции (C¹(I₀)).

 ={x=(x₁( ), x₂()), I₀}.

u₀==u₀( ).

2) Для любой точки(x,u)D:

ивD.

3) Проекция характеристик, выходящих из кривой, ни в одной своей точке не касается кривой , или, что то же самое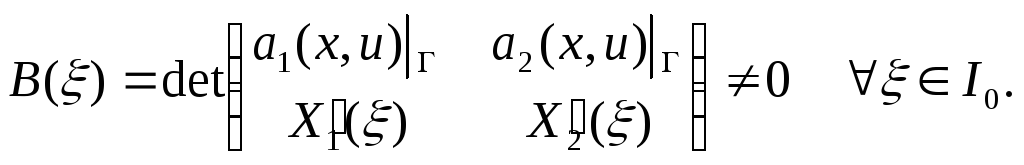

.

Тогдав некоторой достаточно малой окрестностиV_ ( )кривойрассматриваемый выше алгоритм определяет 1 раз дифференцируемую функцию.

V_ ( )={x=X( , ),   I₀,  I_ , и J( , )0}.

Доказательство.

Доказательство следует из курсов О.Д.У., математического анализа, а также из формул алгоритма, а именно:

1) ФункцииX( , ), U( , )(из первого и второго пунктов алгоритма) существуют, 1 раз дифференцируемы по и по в силу теорем О.Д.У. о существовании решения задачи Коши и о дифференцировании решения задачи Коши по параметру.

2) Функции (x) и  (x) существуют и принадлежатC¹ при выполнении условия (*) по теореме об обратной функции.

3) Покажем, что выполняется условие (*), а именно:

покажем, что в

Для этого воспользуемся 3-им условием теоремы:

J( , )0 при =0  по формулам математического анализаD’I₀: в этой окрестностиJ( , )0.

Положим . В этой области будет выполняться (*). Тем самым, в силу последнего пункта алгоритма функцияu(x)=[U( (x), (x))] является один раз дифференцируемой, как композиция двух дифференцируемых функций.

Теорема 2 (о корректности алгоритма для линейного уравнения).

Рассмотрим многомерное линейное уравнение:

, где гладкая гиперповерхность в, т.е. ={x=X( )=X(₁,…,_n-1), =(₁,…,_n-1)I₀},rang=n-1 I₀.

Пусть:

1)  и u₀C¹, т.е. u₀( )C¹(I₀), X( )C¹(I₀).

2) Коэффициенты уравненияa(x), b(x), f(x)C¹(D), D  R¹ ( D).

Причем a(x)0  xD, т.е. векторное поле не имеет точек покоя.

3) Векторное поле характеристической системы нив 1 точке гиперповерхностине касается этой поверхности, т.е.l₁( ),…,l_n-1( ), a(X( )) – линейно независимы, т.е.

Тогдарассматриваемый алгоритм, описанный подробно для случаяn=2,получается заменой на=( ₁,…, _n-1) и определяет в достаточно малой окрестностиV_ ( ) 1 раз дифференцируемую функцию, гдеV_ ( )={x=X( , ), I₀, I_ , J( , )0}.

Доказательство аналогичное.