Интерпретация алгоритма в фазовом пространстве.

Начальному условию S₀(x)можно поставить в соответствие кривую¹в фазовом пространстве:

.

А семейству характеристик в формуле (4) сопоставить кривую¹(t) в фазовом пространстве:

.

кривая¹(t)однозначно проектируется на конфигурационное пространство, т.е. на ней нет точек с вертикальной касательной.

Рисунок приведен для случая предыдущего примера.

Пусть теперь (*) нарушается. Тогда, например, в предыдущем примере при<0, получится следующая картина.

§7. Обоснования алгоритмов решения задачи Коши для уравнения Гамильтона-Якоби

Замечание 1.

Перед изучением данного параграфа желательно изучить приложение к данным лекциям, в котором написаны алгоритмы решения стационарного и нестационарного уравнений Гамильтона-Якоби, а также изложены формулировки теорем о корректности этих алгоритмов.

Замечание 2.

В силу формулы (6) при выполнении условия (*), S(x,t) является гладкой (1 раз дифференцируемой) функцией, что следует из теорем О.Д.У., теоремы о неявной функции и формул алгоритма.

Покажем, что S удовлетворяет начальным условиям:

, что и требовалось.

Лемма Гамильтона.

Импульс на траектории есть градиент решения S, т.е.:

, гдеS(x,t) определяется формулой (6).

В силу условия (*) x₀  x  t, x=X(x₀,t) – луч.

Доказательство.

Докажем только для n=1.

Продифференцируем тождество (2) по параметру x₀.

 в силу (*) 

Лемма доказана.

Доказательство корректности алгоритма.

То, что S удовлетворяет начальным условиям, уже было доказано.

Докажем, что S удовлетворяет уравнению Гамильтона-Якоби.

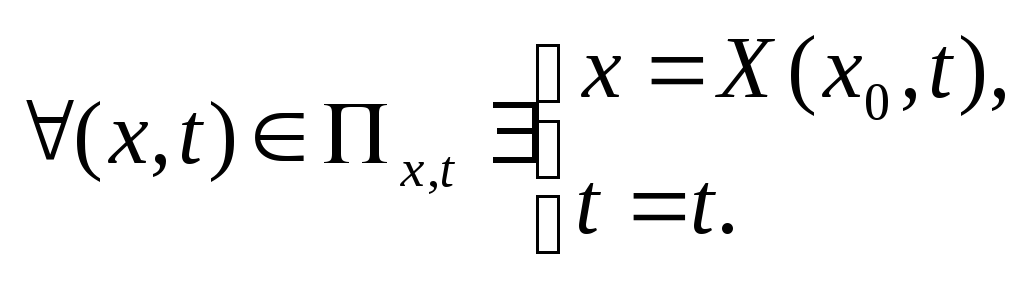
Перейдем от (x,t) к(x₀ ,t), т.е. вернемся к формуле (2):

В силу леммы Гамильтона

 уравнение Гамильтона-Якоби выполнено  t,  x=X(x₀ ,t). Теорема доказана.

Упражнение (единственность решения задачи Коши).

Самостоятельно продумать вопрос единственности решения этой задачи Коши.

Замечание 3 (обобщенное уравнение Гамильтона-Якоби).

Если уравнение имеет вид , то в указанном выше алгоритме меняются только системы (2) и (3):

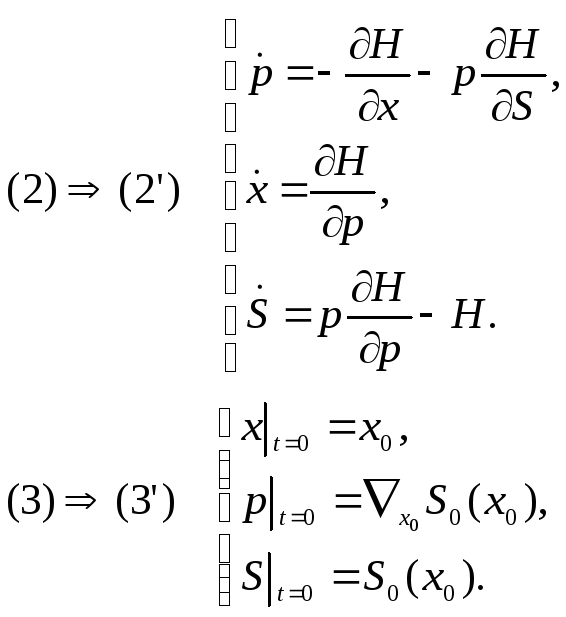
Дальше эту задачу Коши надо решить и найти по формуле , а затем, по формуле (6) найтиS.

Замечание 4 (о стационарном уравнении).

Обоснование алгоритма для стационарного уравнения Гамильтона-Якоби аналогично предыдущему (основано на аналогичной лемме Гамильтона, устанавливаемой в силу дифференцирования формул алгоритма).

Пример (Мираж).

Вопрос: в чем сидит мираж?

Объяснение миража содержится в решении стационарного уравнения Гамильтона-Якоби специального вида:

катастрофа в решении.

H(x,p)=p²-n²(x).

Замечание 5 (о геометрическом смысле леммы Гамильтона).

S₀(x) порождаетn-мерную поверхность в2n-мерном пространстве.

.

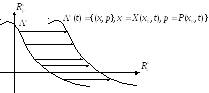
Пусть l_AB ⁿ – гладкая кривая, однозначно проектируемая на. Тогда:

этот интеграл локально не зависит от формы пути. Если поверхностьⁿодносвязная, то слово «локально» можно опустить. Такая поверхность называетсялагранжевой.

Лемма означает, что- также лагранжева поверхность, т.е., т.е. поверхность существует для любого момента времени.

В точках, имеющих вертикальные касательные

, т.е. нарушается условие (*). Такие точки называютсяфокальными.При наличии таких точек уравнениеx=X(x₀,t) может иметь более 1 решения (на рисунке решений 3).

Движение частиц в фазовом пространстве происходит по лагранжевым поверхностям.