5.5 Приклади аудиторних і домашніх задач
1. Які з даних відношень, заданих на множині A={-20,-19,…,0,1,…,19,20} є функціями? Поясніть відповідь.
а) (а,b) R, якщо a=b2;
б) (а,b) R, якщо a2=b;
в) (а,b) R, якщо ab;
г) (а,b) R, якщо ab=6;
д) (а,b) R, якщо b = a3;
е) (а,b) R, якщо a= b3;
ж) (а,b) R, якщо a=6/b.
2. Які з функцій, знайдених під час вирішення завдання 1, є відображеннями виду f: AA?
3. Нехай задані множини A, B, С та відношення RAB й SBC. Покажіть на прикладах, що такі висновки не вірні:
а) якщо R – функція, то SR – функція;
б) якщо R – відображення AB, то SR – відображення AC;
в) якщо S – визначає ін’єкцію ВМ, то SR – ін’єкцію AС.
4. Нехай задано множини A, B, С та відношення RAB та SBC. Доведіть, що:
а) якщо R і S – функції, то SR – функція;
б) якщо R і S – визначають відображення AB й ВС відповідно, то SR – визначає відображення AС;
в) якщо R і S – визначають сюр’єкції, то SR – також сюр’єкцію.
5. Доведіть, що якщо f – ін’єктивна функція, то існує функція f -1.
6. Нехай FXY визначає сюр’єктивну функцію. Чи визначає F -1 відображення XY?
7. Знайдіть область визначення та область значень даних функцій:
а) функція, яка кожному позитивному цілому числу x (xn), ставить у відповідність його останню цифру;
б) функція, котра для цілого позитивного числа x (xn), знаходить найбільший квадрат, який не перевищує це число.
8. Нехай A і B – скінченні множини, які містять відповідно n та m елементів: |A|=n, |B|=m. Визначте співвідношення між n та m, якщо:
а) існує ін’єктивне відображення з A у B;
б) існує сюр’єктивне відображення з A у B.
6 Практичне заняття № 4. Булеві функції та алгебра логіки
6.1 Мета заняття
Ознайомитися з поняттям булевої функції і способами її задання, а також вивчити способи еквівалентних перетворень формул алгебри логіки, використо-вуючи основні закони алгебри логіки.
6.2 Методичні рекомендації до самостійної роботи студентів
Під час підготовки до практичного заняття крім конспекту лекцій рекомендується використовувати [1, c. 99-111, c. 115-120; 2, c. 99-111, c. 115-120; 4, c. 52-58; 9, c. 31-35, c. 37-39; 12, c. 36-54; 17, c. 23-63].
При вивченні і повторенні матеріалу слід звернути увагу на такі питання:
ізоморфізм алгебри множин та булевої алгебри;
булеві змінні, булеві функції;
кількість наборів аргументів і булевих функцій на n булевих змінних;
способи задання булевих функцій;
булеві функції від однієї та двох змінних;
властивості операцій булевих функцій;
елементарні функції алгебри логіки;
закони й тотожності алгебри логіки;
еквівалентні перетворення формул алгебри логіки.
6.3 Приклади розв’язання типових завдань
1. Чи
еквівалентні формули В
і U, якщо
,
?
Перевіримо еквівалентність формул за допомогою таблиць, реалізованих ними функцій.
x |
y |
z |
B |
U |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
Оскільки таблиці функцій не збігаються, формули нееквівалентні.
2.
Доведіть, що число усіх
різноманітних n-місних
булевих функцій дорівнює
.
Набір значень булевої функції являє собою двійковий код, розрядність (m) якого залежить від кількості аргументів функції. Кількість різноманітних комбінацій значень функції від n аргументів 2m, а, в свою чергу, m дорівнює кількості різноманітних наборів значень n двійкових аргументів, тобто m=2n. Таким чином, .
3.
Спростіть вираз:
.
використаємо закон виключного третього:
.
4.
Побудуємо таблицю істинності для
функції, заданої такою формулою
.
Функція залежить від трьох змінних і, отже, для неї є 23=8 інтерпретацій. Для побудови таблиці істинності необхідно визначити значення функції на всіх інтерпретаціях:
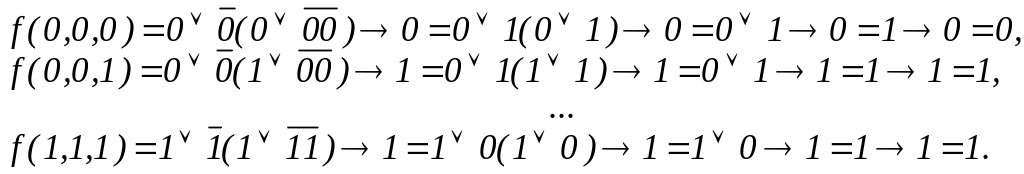
Розмістимо в таблиці істинності інтерпретації в порядку зростання відповідних до них двійкових номерів і запишемо отримане значення функції на кожній інтерпретації. Одержимо таблицю істинності функції
:
x |
y |
z |
f(x,y,z) |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |