3 Практичне заняття № 1. Основні поняття теорії множин. Алгебра множин

3.1 Мета заняття

Метою практичного зайняття є розгляд апарата теорії множин, вивчення операцій теорії множин, а також застосування основних законів теорії множин при вирішенні практичних задач.

3.2 Методичні рекомендації до самостійної роботи студентів

Під час підготовки до практичного заняття необхідно вивчити відповідний розділ конспекту лекцій та ознайомитися з матеріалом підручників [1, c. 9-11; 2, c. 9-11; 3, c. 6-10; 4, c. 8-18; 9, c. 4-11; 12, c. 16-35; 15, c. 7-13; 17, c. 7-22].

При повторенні матеріалу слід звернути увагу на такі питання:

• основні визначення;

• способи задання множин;

• операції над множинами;

• рівність множин;

• підмножини;

• потужність множин;

• скінченні і нескінченні множини;

• застосування апарата теорії множин;

• формули і тотожності алгебри множин;

• еквівалентні перетворення формул;

• геометрична інтерпретація множин: кола Ейлера та діаграми Венна.

3.3 Приклади розв’язання типових завдань

1. Проілюструвати за допомогою діаграм Венна таку формулу: E=А\(ВС).

Виконуючи дію у дужках (ВС)=Е`, одержимо діаграму, зображену на рис. 3.1 а.

Після цього будуємо А\Е`, тобто необхідно виділити частину множини А, що не належить множині Е. Відповідь зображена на рис. 3.1 б.

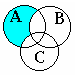
а б

Рисунок 3.1

2. Записати множину , якщо А={2,4,6,8,10,12}, B={3,6,9,12}.

Знайдемо множину А\В={2,4,8,10}. Для одержання остаточної відповіді потрібно виконати операцію доповнення, тобто множина Е складатиметься з елементів множини В: Е={3,6,9,12}.

3. За діаграмою Венна (рис. 3.2) записати формулу:

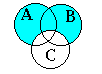
Рисунок 3.2

Запишемо спочатку АВ (рис. 3.3 а), потім (АВ) \С (рис. 3.3 б).

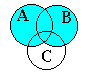
а б

Рисунок 3.3

4. Довести A\(A\B)=AB.

.

За законом Де-Моргана і законом дистрибутивності:

5. Довести, що , де А та В – множини.

- відповідно до визначення операції різниці.

Підставимо вираз у формулу і винесемо А за дужки:

.

4. Контрольні запитання та завдання

1. Наведіть приклади скінченних та нескінченних множин.

2. Яка множина називається упорядкованою?

3. Проілюструйте на прикладах геометричну інтерпретацію множин.

4. Назвіть властивості операцій над множинами.

5. Назвіть відомі вам способи задання множин. У якому випадку неможливо застосувати той чи інший спосіб?

6. Чи можуть два елементи однієї множини бути рівними?

7. Чим відрізняється строге включення від нестрогого? Наведіть приклади.

8. Як визначається рівність множин через поняття нестрогого включення?

9. Розташуйте операції алгебри множин відповідно до їх пріоритету.

10. Назвіть тотожності алгебри множин, запишіть відповідні їм формули.

3.5 Приклади аудиторних і домашніх задач

1. За допомогою діаграм Венна проілюструйте такі співвідношення:

а) A\(BC)=(A\B) (A\C);

б) (A\B) \C=A\(BC);

в) (AB) \C=(A\C) (B\C);

г) (AB) \C=(A\C)  (B\C).

2. Задайте переліком елементів такі множини:

a) множину натуральних чисел, не більших 7;

б) множину простих чисел між 10 та 20;

в) множину позитивних чисел, кратних 12;

г) множину літер вашого імені;

д) множину, єдиним елементом якої є назва вашого міста.

3. Перерахуйте елементи множин:

a) {x | xN,3x12};

б) {x | x – десяткова цифра};

в) {x | x=2 чи x=5}.

4. Нехай A, B і C – множини. Покажіть, що:

а) (AB)A;

б) A(AB);

в) (AB) (ABC).

5. Спростіть вираз:

а) ;

б) ;

в) ;

г) ;

д) .

25. У якому відношенні знаходяться множини A та B, якщо A\B=B\A=?

26. Доведіть:

а) , де А та В – множини;

б) ;

в) ;

г) ;

д) .