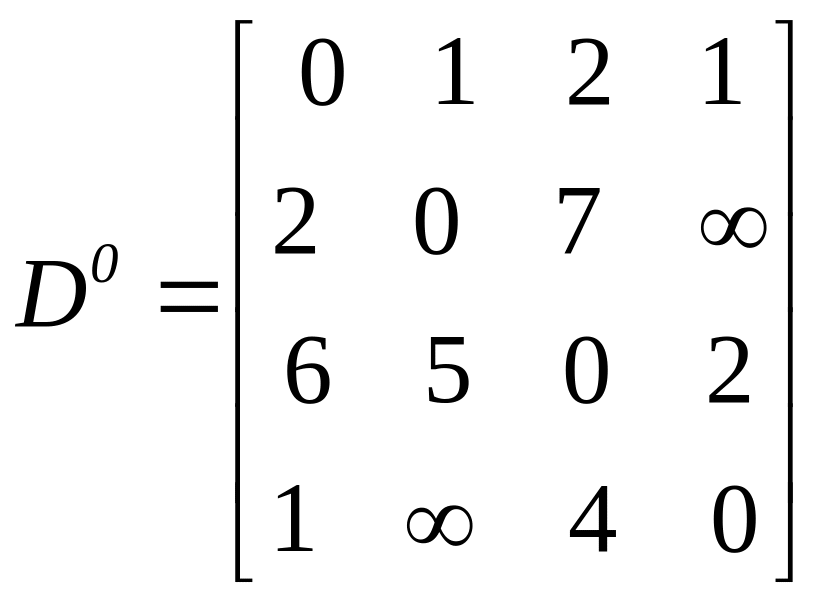- •1 Мета і задачі дисципліни
- •1.1 Мета викладання дисципліни
- •1.2 Програма знань і вмінь
- •1.3 Теми практичних занять
- •1.4 Система атестації
- •Без виконання усіх без винятку пунктів табл. 1.2 студент до іспиту допущений не буде. Оцінка виставляється, виходячи з табл. 1.3.
- •2 Огляд рекомендованої літератури
- •3 Практичне заняття № 1. Основні поняття теорії множин. Алгебра множин
- •3.1 Мета заняття
- •3.2 Методичні рекомендації до самостійної роботи студентів
- •3.3 Приклади розв’язання типових завдань
- •Контрольні запитання та завдання
- •3.5 Приклади аудиторних і домашніх задач
- •4 Практичне заняття № 2. Відношення та їх властивості
- •4.1 Мета заняття
- •4.2 Методичні рекомендації до самостійної роботи студентів
- •4.3 Приклади розв’язання типових завдань
- •4.4 Контрольні запитання та завдання
- •4.5 Приклади аудиторних і домашніх задач
- •5 Практичне заняття № 3. Відображення та функції
- •5.1 Мета заняття
- •5.2 Методичні рекомендації до самостійної роботи студентів
- •5.3 Приклади розв’язання типових завдань
- •5.4 Контрольні запитання та завдання
- •5.5 Приклади аудиторних і домашніх задач
- •6 Практичне заняття № 4. Булеві функції та алгебра логіки
- •6.1 Мета заняття
- •6.2 Методичні рекомендації до самостійної роботи студентів
- •6.3 Приклади розв’язання типових завдань
- •6.4 Контрольні запитання та завдання
- •6.5 Приклади аудиторних і домашніх задач
- •7 Практичне заняття № 5. Двоїстість булевих функцій
- •7.1 Мета заняття
- •7.2 Методичні рекомендації до самостійної роботи студентів
- •7.3 Приклади розв’язання типових завдань
- •7.4 Контрольні запитання та завдання
- •7.5 Приклади аудиторних і домашніх задач
- •8 Практичне заняття № 6. Нормальні форми
- •8.1 Мета заняття
- •8.2 Методичні рекомендації до самостійної роботи студентів
- •8.3 Приклади розв’язання типових завдань
- •8.4 Контрольні запитання та завдання
- •8.5 Приклади аудиторних і домашніх задач
- •9 Практичне заняття № 7. Алгебра жегалкіна
- •9.1 Мета заняття
- •9.2 Методичні рекомендації до самостійної роботи студентів
- •9.3 Приклади розв’язання типових завдань
- •9.4 Контрольні запитання та завдання
- •9.5 Приклади аудиторних і домашніх задач
- •10 Практичне заняття № 8. Функціональна повнота наборів булевих функцій
- •10.1 Мета заняття
- •10.2 Методичні рекомендації до самостійної роботи студентів
- •10.3 Приклади розв’язання типових завдань
- •10.4 Контрольні запитання та завдання
- •10.5 Приклади аудиторних і домашніх задач
- •11 Практичне заняття № 9 методи мінімізації булевих функцій
- •11.1 Мета заняття
- •11.2 Методичні рекомендації до самостійної роботи студентів
- •11.3 Приклади розв’язання типових завдань
- •11.4 Контрольні запитання та завдання
- •11.5 Приклади аудиторних і домашніх задач
- •12 Практичне заняття № 10. Логіка висловлювань
- •12.1 Мета заняття
- •12.2 Методичні рекомендації до самостійної роботи студентів
- •12.3 Приклади розв’язання типових завдань
- •12.4 Контрольні запитання та завдання
- •12.5 Приклади аудиторних і домашніх задач
- •13 Практичне заняття № 11. Логіка першого порядку (лпп)
- •13.1 Мета заняття
- •13.2 Методичні рекомендації до самостійної роботи студентів
- •13.3 Приклади розв’язання типових завдань
- •13.4 Контрольні запитання та завдання
- •13.5 Приклади аудиторних і домашніх задач
- •14 Практичне заняття № 12. Основні поняття теорії графів
- •14.1 Мета заняття
- •14.2 Методичні рекомендації до самостійної роботи студентів
- •14.3 Приклади розв’язання типових завдань
- •15 Практичне заняття № 13. Ейлерові і гамільтонові ланцюги і цикли
- •15.3 Приклади розв’язання типових завдань
- •15.4 Контрольні запитання та завдання
- •15.5 Приклади аудиторних і домашніх задач
- •16 Практичне заняття № 14. Планарність графів
- •16.1 Мета заняття
- •16.2 Методичні рекомендації до самостійної роботи студентів
- •16.3 Приклади розв’язання типових завдань
- •16.4 Контрольні запитання та завдання
- •16.5 Приклади аудиторних і домашніх задач
- •17 Практичне заняття № 15. Відстані на графах
- •17.1 Мета заняття
- •17.2 Методичні рекомендації до самостійної роботи студентів
- •17.3 Приклади розв’язання типових завдань
- •17.4 Контрольні запитання та завдання
- •17.5 Приклади аудиторних і домашніх задач
- •18 Практичне заняття № 16. Дерева
- •18.1 Мета заняття
- •18.2 Методичні рекомендації до самостійної роботи студентів
- •18.3 Приклади розв’язання типових завдань
- •18.4 Контрольні запитання
- •18.5 Приклади аудиторних і домашніх задач
- •19 Практичне заняття № 17. Транспортні мережі
- •19.1 Мета заняття
- •19.2 Методичні рекомендації до самостійної роботи студентів
- •19.3 Приклади розв’язання типових завдань
- •19.4 Контрольні запитання та завдання
- •19.5 Приклади аудиторних і домашніх задач
- •20 Практичне заняття № 18. Основи комбінаторного аналізу
- •20.1 Мета заняття
- •20.2 Методичні рекомендації до самостійної роботи студентів
- •20.3 Приклади розв’язання типових завдань
- •20.4 Контрольні запитання та завдання
- •20.5 Приклади аудиторних і домашніх задач
- •21 Практичне заняття № 19. Формули простого перелічення
- •21.1 Мета заняття
- •21.2 Методичні рекомендації до самостійної роботи студентів
- •21.3 Приклади розв’язання типових завдань
- •21.4 Контрольні запитання та завдання
- •21.5 Приклади аудиторних і домашніх задач
- •22 Практичне заняття № 20. Формула включення та виключення
- •22.1 Мета заняття
- •22.2 Методичні рекомендації до самостійної роботи студентів
- •22.3 Приклади розв’язання типових завдань
- •22.4 Контрольні запитання та завдання
- •22.5 Приклади аудиторних і домашніх задач
- •23 Індивідуальні контрольні завдання
- •Завдання 9. У табл. 23.7 ребрам (Vj, Vk) неорієнтованого графа, що задані номерами вершин j та k, вiдповiдає числова характеристика (довжина, вартість).
- •Рекомендована література
16.4 Контрольні запитання та завдання
1. Який граф називається плоским?
2. Що називається гранню графа?
3. Що таке підрозбиття ребер графа?
4. Який граф називається планарним?
5. Критерії планарності графа. Критерій Понтрягина-Куратовського, критерій Вагнера.
6. Яка вершина називається контактною? Наведіть приклад.
7. Доведіть, що сума ступенів вершин графа дорівнює подвоєній кількості його ребер.
8. Доведіть, що граф з п'ятьма вершинами, одна з яких має ступінь 2, є планарним.
9. Покажіть, що якщо графи G1 та G2 – ізоморфні, то вони мають однакову кількість вершин і ребер.
10. Доведіть, що довільний граф з чотирма вершинами є планарним.
16.5 Приклади аудиторних і домашніх задач
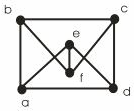
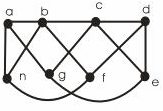
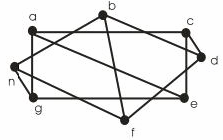
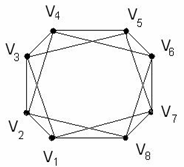
1. Скільки граней містять дані графи (рис. 16.11)?
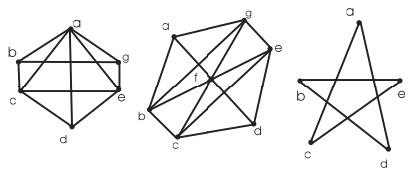
Рисунок 16.11
2. Визначте, який з графів G1,G2, G3 (рис. 16.12) є гомеоморфним до G:
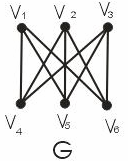
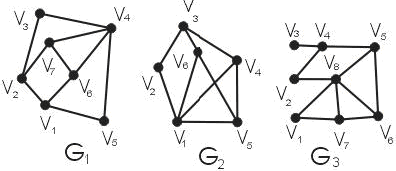
Рисунок 16.12
3. Для кожного планарного графа (рис. 16.11), перевірити, чи виконуються умови m-n+f=0, де m – кількість вершин графа, n – кількість ребер, f – кількість граней.
4. Кожен з наведених графів (рис. 16.13) перевірте на планарність, аргументуйте рішення.
|
|
|
Рисунок 16.13
5. Розмістіть граф на тор (рис. 16.14).
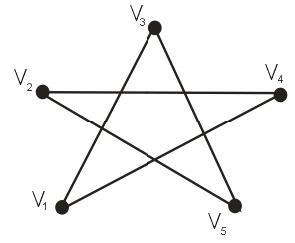
Рисунок 16.14
6. Зобразити графи, ізоморфні даним (рис. 16.15).
|
|
Рисунок 16.15
17 Практичне заняття № 15. Відстані на графах
17.1 Мета заняття
Ознайомитися з поняттям відстані на графах та навчитися використо-вувати алгоритм Дейкстри для знаходження відстаней на графах.
17.2 Методичні рекомендації до самостійної роботи студентів
Під час підготовки до практичного заняття необхідно вивчити відповідний розділ конспекту лекцій та ознайомитися з матеріалом підручників [1, c. 292-304; 2, c. 292-304; 17, c. 64-128].
При повторенні матеріалу слід звернути увагу на такі питання:
аксіоми метрики;
графи з числовими характеристиками ребер (дуг);
відстань між двома вершинами на графі;
алгоритм визначення відстані між вершинами на графі з одиничними довжинами ребер;
алгоритм Дейкстри визначення відстані між вершинами на графі з довільними довжинами ребер.
17.3 Приклади розв’язання типових завдань
1.
Для графа, зображеного на рис. 17.1,
необхідно знайти відстані від вершини
![]() до всіх інших вершин по алгоритму
Дейкстри. Знайти найкоротший шлях з
у
до всіх інших вершин по алгоритму
Дейкстри. Знайти найкоротший шлях з
у
![]() .
.
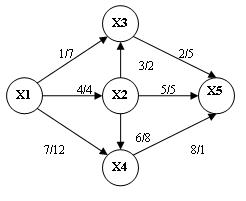
Рисунок 17.1
Цикл
1. Біля кожної вершини
ставимо її тимчасову позначку, позначка
вершини
– (0,1) постійна, її підкреслюємо. Знаходимо
вершину
![]() ,
у якої перша позиція тимчасової позначки
4 – найменша. Вважаємо позначку цієї
вершини постійною, підкреслюємо її.
,
у якої перша позиція тимчасової позначки
4 – найменша. Вважаємо позначку цієї
вершини постійною, підкреслюємо її.
Цикл
2. Знаходимо
вершини
![]() ,
,
![]() та
,
в які заходять дуги, вихідні з
.
Оскільки 4+2<7 та 4+5<
та
,
в які заходять дуги, вихідні з
.
Оскільки 4+2<7 та 4+5<![]() ,
то тимчасові позначки вершин
і
виправляємо на (6,2) і (9,2) відповідно.
Тимчасову позначку вершини
не змінюємо. Далі знаходимо
вершину
,
у
якої перша позиція тимчасової
позначки 6 – найменша. Позначку цієї
вершини оголошуємо
постійною
й підкреслюємо її.
,
то тимчасові позначки вершин
і
виправляємо на (6,2) і (9,2) відповідно.
Тимчасову позначку вершини
не змінюємо. Далі знаходимо
вершину
,
у
якої перша позиція тимчасової
позначки 6 – найменша. Позначку цієї
вершини оголошуємо
постійною
й підкреслюємо її.
Цикл 3. Знаходимо вершину , в яку заходить дуга, вихідна з вершини . Оскільки 6+2<9, пишемо нову тимчасову позначку цієї вершини (8,3). Знаходимо вершину , у якій перша позиція тимчасової позначки 6 – найменша. Її позначку оголошуємо постійною.
Цикл 4. Переконуємося, що з вершини не виходять дуги. Виходячи з цього, тимчасові позначки, що залишилися, виправляти не слід. Знаходимо єдину вершину, що має тимчасову позначку – . Оголошуємо її позначку постійною.
Алгоритм закінчено: d( , )=4; d( , )=6; d( ; )=8; d( , )=12.
Використовуючи другі позиції постійних позначок, визначимо найкоротший шлях з в : .
Застосуємо алгоритм Данцига для пошуку найкоротших шляхів між усіма парами вершин графа, зображеного на рис. 17.2. Матриця D°, складена з довжин дуг цього графа, наведена на рис. 17.2.
|
|
Рисунок 17.2
Очевидно,
![]() .
Величини елементів матриці D2знаходяться
так:
.
Величини елементів матриці D2знаходяться
так:
Елементи |
Відповідний шлях |
|
|
|
(1, 2) |
|
|
|
(2, 1) |
Величини елементів матриці D3 знаходяться так:
Елементи |
Відповідний шлях |
|
(1, 3) |
|
(2, 1), (1, 3) |
|
(3, 1) |
|
(3, 2) |
|
(1, 2) |
|
(2, 1) |
|
|
Отже,
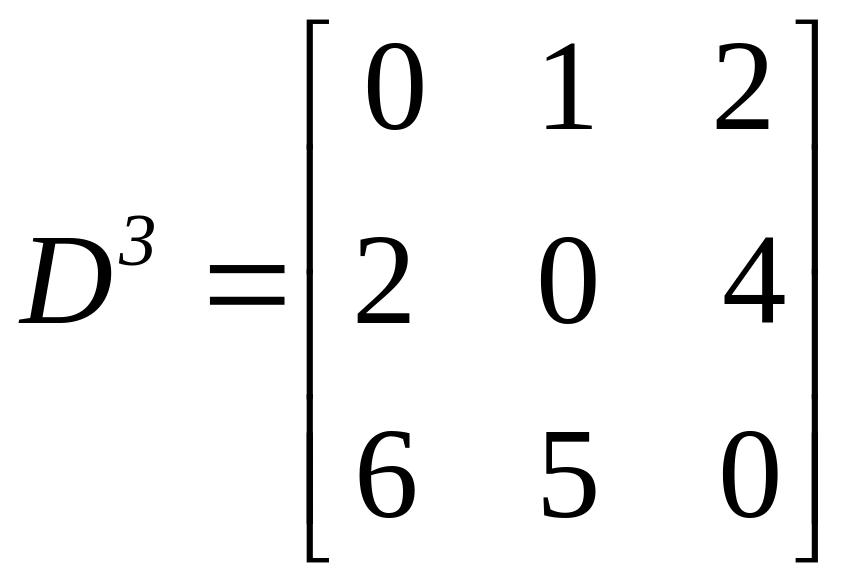
Відповідна матриця найкоротших шляхів має вигляд:
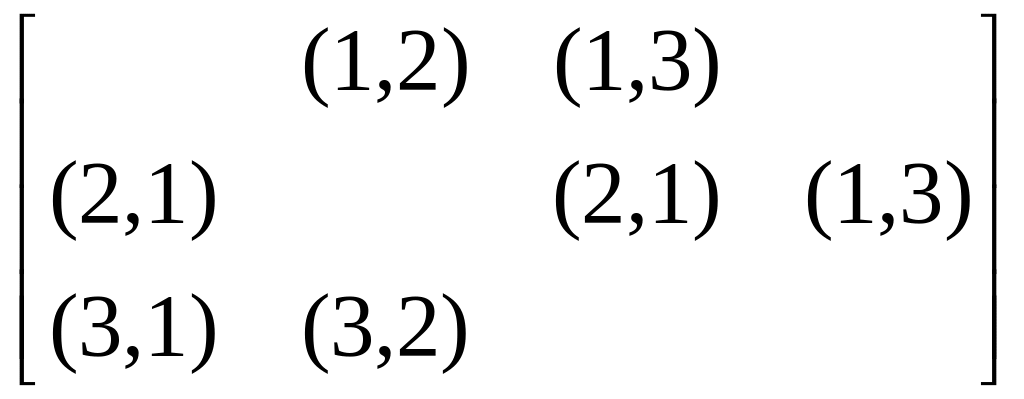
Для
завершення розрахунків залишається
повторити процедуру (зробити самостійно)
пошуку
![]() для m = 4.
для m = 4.