15.5 Приклади аудиторних і домашніх задач
1. Які з даних графів є ейлеровими (гамільтоновими) (рис. 15.7)?
2. У наведених графах (рис. 15.7) знайти ейлерові (гамільтонові) ланцюги та цикли, якщо такі існують. Визначіть, скільки і які ребра потрібно додати у кожен граф, щоб можна було одержати ейлерів (гамільтонів) ланцюг чи цикл за їхньої відсутності.
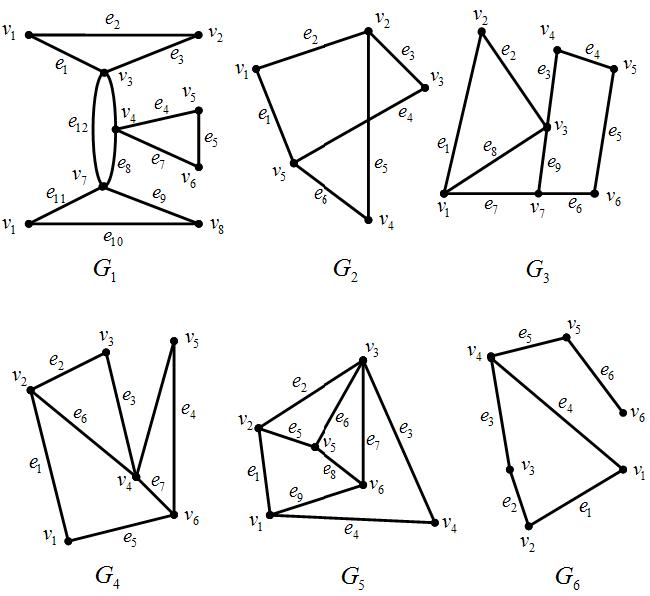
Рисунок 15.7
3. Розбити квадрат на дрібніші квадрати прямими, рівнобіжними до його сторін (нижче наведений приклад у випадку n=3 (рис. 15.8)). Чи мають такі графи гамільтонові ланцюги чи цикли?
Рисунок 15.8
4. У заданому орієнтованому графі знайдіть гамільтонів цикл та 2–3 гамільтонові ланцюги (рис. 15.9).
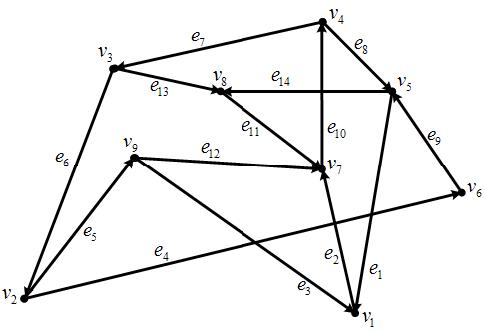
Рисунок 15.9
16 Практичне заняття № 14. Планарність графів
16.1 Мета заняття
Ознайомитися з поняттями плоского і планарного графів. Навчитися будувати плоске укладення для заданого графа.
16.2 Методичні рекомендації до самостійної роботи студентів
Піж час підготовки до практичного заняття необхідно вивчити відповідний розділ конспекту лекцій та ознайомитися з матеріалом підручників [1, c. 242; 2, c. 242; 8, c. 126-151; 12, c. 316-317; 17, c. 64-128].
При повторенні матеріалу слід звернути увагу на такі питання:
плоскі, планарні та гомеоморфні графи;
теорема Понтрягіна-Курантовського;
теореми про особливості планарних графів;
Жорданова крива;
побудова плоского укладення графа.
16.3 Приклади розв’язання типових завдань
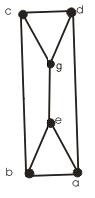
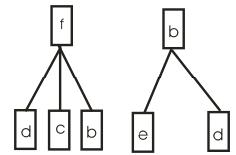
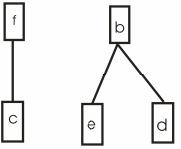
1. Зобразити граф, ізоморфний графу G (рис. 16.1).
Під час побудови ізоморфного графа не має значення послідовність перетворення. Головне, щоб виконувалися умови ізоморфізму.
Почнемо з того, що повернемо граф G на 90 градусів (рис. 16.2).
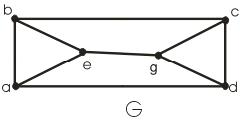
Рисунок 16.1
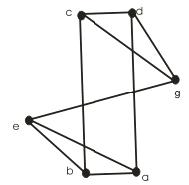
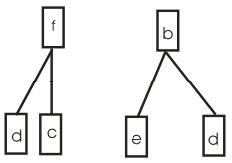
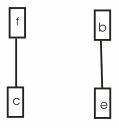
Тепер винесемо вершини e та g за межі прямокутника, утвореного ребрами, інцидентними вершинам a, b, c, d (рис. 16.3).
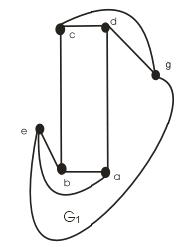
Заберемо з даного графа перетинання ребер, тим самим зробивши його плоским. Пустимо ребро ae за вершиною b, скрививши його. Те саме зробимо з ребрами cg та eg, після чого граф стане плоским та ізоморфним (рис. 16.4).
Рисунок 16.2
|
Рисунок 16.3
|
Рисунок 16.4 |
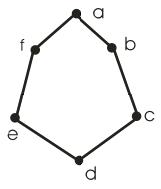
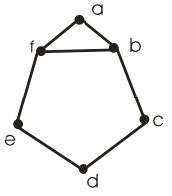
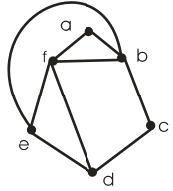
3. Перевірити граф G (рис. 16.5) на планарність.
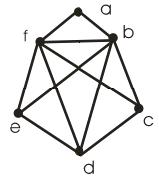
Рисунок 16.5
Відповідно до визначення, граф, ізоморфний плоскому, називається планарним, тобто якщо побудувати плоске розміщення укладення графа G, то він буде планарним.
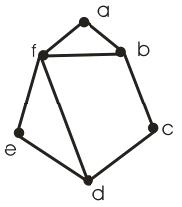
Вибираємо простий цикл у графі G, після чого рисуємо сегменти, що залишилися не задіяні (рис. 16.6). Тепер вибираємо найбільший сегмент і розміщуємо його частину так, щоб утворилася ще одна грань. У цьому випадку такою частиною буде ребро fb (рис. 16.7).
Рисунок 16.6 |
Рисунок 16.7 |
Тепер залишилося два рівних сегменти, тому вибираємо будь-який з них і також розміщуємо його частину так, щоб вийшла ще одна грань (рис. 16.8).
Після цього вийшов один сегмент з двома вершинами і один – з трьома. Вибираємо більший. Знов укладаємо його частину так, щоб з'явилася ще одна грань у графі (рис. 16.9).
Рисунок 16.8 |
Рисунок 16.9 |
Тепер вийшло знов два однакових сегменти, після укладення яких одержимо плоский граф G’, який зображено на рисунку 16.10. Оскільки можливо зробити плоске укладення графа G, то він є планарним.
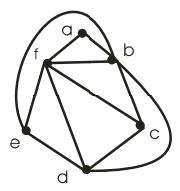
Рисунок 16.10