11.4 Контрольні запитання та завдання

1. У чому полягає задача мінімізації булевих функцій? У чому особливість її канонічної форми?

2. Дайте визначення поняттю імпліканти (імпліценти) булевої функції.

3. Що являє собою повна система імплікант (імпліцент)?

4. Яка імпліканта (імпліцента) називається простою?

5. Дайте визначення скороченої, тупикової та мінімальної ДНФ (КНФ)?

6. Що являє собою карта Карно (діаграма Вейча)?

7. Сформулюйте правило склеювання клітинок і запису мінімальної ДНФ методом карт Карно.

8. У чому відмінність застосування діаграм Вейча для мінімізації на множині КНФ від карт Карно?

9. Як здійснюється мінімізація частково визначених функцій?

11.5 Приклади аудиторних і домашніх задач

1. Побудувати карти Карно для функцій:

а) ;

б) ;

в) ;

г) ;

д) .

2. Знайти мінімальні КНФ (ДНФ) для функцій, які задані такими діаграмами Вейча (картами Карно):

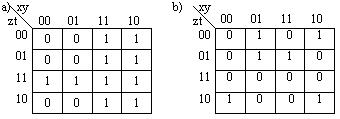
3. Знайти мінімальні ДНФ (КНФ) частково заданої функції, які задано такими картами Карно (діаграмами Вейча):

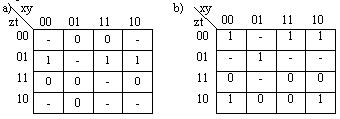
13. Мінімізувати методом карт Карно (діаграм Вейча) та знайти мінімальну ДНФ (КНФ) функції, яка має значення F=1 на наборах:

а) {0,1,2,5,6,11,13,15};

б) {1,2,3,4,6,7,8,9,12,13,14}.

в) {0,1,2,5,6,11,13,15};

г) {1,2,3,4,6,7,8,9,12,13,14}.

12 Практичне заняття № 10. Логіка висловлювань

12.1 Мета заняття

Ознайомитися з математичним апаратом логіки висловлювань. Навчитися формалізувати речення природної мови.

12.2 Методичні рекомендації до самостійної роботи студентів

Під час підготовки до практичного заняття необхідно вивчити відповідний розділ конспекту лекцій та ознайомитися з матеріалом підручників [1, 183-207; 2, c. 183-207; 3, c. 47-50, c. 73-78; 9, c. 64-82; 15, c. 46-68; 15, 2 c. 3-63].

При повторенні матеріалу слід звернути увагу на такі питання:

• поняття висловлювання, атома, молекули, формули;

• логічні зв'язки, область дії логічних зв'язок;

• побудова складних формул;

• загальнозначущі і суперечливі формули;

• істинність значення висловлення;

• інтерпретація формул у логіці висловлювань;

• логічні висновки, теореми про логічні наслідки.

12.3 Приклади розв’язання типових завдань

1. Розглянемо формулу G=(PQ)(R~(S)).

Атомами у цій формулі є Р, Q, R і S. Припустимо, що істинностні значення Р, Q, R та S дорівнюють І, Х, І та І відповідно. Тоді:

• (РQ) має значення Х, оскільки Q хибна;

• (S) має значення Х, оскільки S має значення І;

• (R~(S)) має значення Х, оскільки R має значення І та (S) має значення Х;

• (PQ)(R~(S)) має значення Х, тому що (PQ) має значення Х та (R~(S)) має значення Х.

Таким чином, формула G має значення І, якщо атомам Р, Q, R та S приписані значення І, Х, І та І відповідно.

2. Студент у день іспиту вирішив встати раніше, зробити зарядку, після іспиту здати книжки в бібліотеку або сходити в кінотеатр і, якщо добре складе іспит, сходити у дискотеку. Використовуючи апарат логіки висловлювань, визначити, в якому випадку план студента не буде виконаний.

Виділяємо прості висловлення у складі вхідного складного:

X: «Студент у день іспиту встав раніше»;

Y: «Студент у день іспиту зробив зарядку»;

Z: «Студент після іспиту здав книжки в бібліотеку»;

T: «Студент після іспиту сходив у кінотеатр»;

U: «Студент склав іспит добре»;

V: «Студент після іспиту сходив у дискотеку».

Формула вхідного складного висловлення: .

План студента виконаний, якщо значення цього складного висловлювання дорівнює 1. Якщо план студента не виконаний, то значення цього складного висловлювання дорівнює 0, а його заперечення – 1:

Підставляючи замість змінних прості висловлювання, одержимо відповідь на запитання. Вона відповідає інтуїтивному розумінню ситуації.

4. Якщо студент не береться за підручники і конспекти, то він не складе сесію, якщо тільки це не відбувається під час канікул і студент не відпочиває. Чи складе студент сесію, якщо він не вчиться, а це відбувається під час семестру?

Для знаходження відповіді засобами алгебри логіки перетворимо твердження в символи:

X: "Студент береться за підручники і конспекти (не вчиться)";

Y: "Студент складає сесію успішно";

Z: "Справа відбувається під час канікул";

T: "Студент відпочиває".

Викладені факти можуть бути подані такими формулами:

F₁: : – "Якщо студент не вчиться, то він не складає сесію, якщо тільки це відбувається не в сесію і студент не відпочиває";

F₂: – "Студент не вчиться";

F₃: – "Справа відбувається під час семестру".

Для відповіді на запитання необхідно перевірити, чи є логічним наслідком фактів F₁, F₂, F₃, тобто чи є формула тотожно істинною. Підставляючи всі можливі значення X, Y, Z і T у формулу, переконаємося, що ця формула дорівнює 1 за будь-яких істиннісних значень вхідних у неї змінних. Тому є логічний наслідок F₁, F₂ і F₃. Отже, студент не складе сесію.

6. Розглянемо формули F₁=(PQ), F₂=Q, G=P. Покажемо, що G є логічним наслідком F₁ і F₂.

Доведемо, що ((РQ)Q)((Р))=((РQ)Q)Р суперечлива.

Доведемо суперечливість формули (РQ)QР шляхом її перетворення у диз'юнктивну нормальну форму:

(РQ)QР=(РQ)QР=(РQР)(QQР)=00=0

Таким чином, Р суперечлива. Отже, G є логічний наслідок F₁ та F₂.

7. Використовуючи теорему дедукції, довести, що АВ, ВС├АС.

Для доведення достатньо показати, що АВ, ВС, АС

(х₁) АВ (вихідна формула);

(х₂) ВС (вихідна формула);

(х₃) А (вихідна формула);

(х₄) В (за схемою висновку з x₁ та x₃);

(х₅) С (за схемою висновку з x₂ та x₄);

(х₆) АС (за теоремою дедукції з х₁, х₂, х₃, х₄, х₅).