II.4. Решение слау с помощью -разложения

Пусть – данная матрица, a и – соответственно нижняя и верхняя треугольные матрицы. Справедливо следующее утверждение.

Теорема 2.1. Если все главные миноры квадратной матрицы отличны от нуля, то существуют такие нижняя и верхняя треугольные матрицы, что . Если элементы диагонали одной из матриц или фиксированы (ненулевые), то такое разложение единственно.

Вместо полного доказательства этой теоремы получим формулы для фактического разложения матриц в случае фиксирования диагонали нижней треугольной матрицы .

Будем находить (при ) и (при ) такие, чтобы

.

Выполнив перемножение матриц, на основе поэлементного приравнивания левых и правых частей приходим к их -матрице уравнений

, , …, ,

, , …, ,

…………, …………………, …, ...………………..,

, , …, ,

относительно -матрицы неизвестных

(2.6)

Специфика этой системы позволяет находить неизвестные (2.6) одно за другим в следующем порядке. Из первой строки уравнений имеем

;

из оставшейся части первого столбца уравнений

;

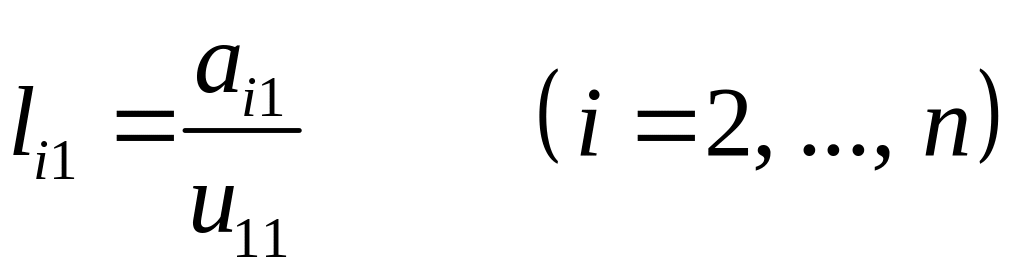из оставшейся части второй строки

;

из оставшейся части второго столбца

и т.д. Последним находится элемент

.

Легко видеть, что все отличные от 0 и 1 элементы матриц и могут быть однозначно вычислены с помощью всего двух формул:

, (2.7)

. (2.8)

При практическом выполнении разложения (применимы также термины факторизация, декомпозиция) матрицы нужно иметь в виду следующие два обстоятельства.

Во-первых, организация вычислений по формулам (2.7)–(2.8) должна предусматривать переключение счета с одной формулы на другую в соответствии с показанным выше процессом получения неизвестных, приведшим к этим формулам. Это удобно делать, ориентируясь на матрицу неизвестных (2.6), а именно, первая строка (2.6) вычисляется по формуле (2.7) при , ; первый столбец (2.6) (без первого элемента) – по формуле (2.8) при , , и т.д.

Во-вторых, препятствием для осуществимости описанного процесса –разложения матрицы может оказаться равенство нулю диагональных элементов матрицы , поскольку на них выполняется деление в формуле (2.8). Отсюда требование теоремы, накладываемое на главные миноры (напомним, что главными минорами матрицы называются определители подматриц , где ). Заметим, что первый диагональный элемент матрицы совпадает с первым главным минором и по условию должен быть отличным от нуля. Второй диагональный элемент матрицы

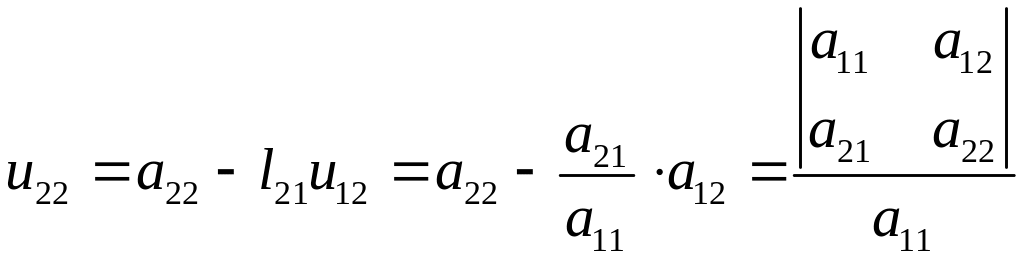
не равен нулю, если отличен от нуля второй главный минор, и т.д. Ясно, что вместо проверки на равенство нулю главных миноров данной матрицы удобнее делать такую проверку для элементов в процессе их вычисления, причем, чтобы уменьшить влияние погрешностей округлений, лучше сравнивать модули с малой положительной константой (допуском). Для определенных классов матриц требования теоремы о разложении заведомо выполняются. Это относится, например, к матрицам с диагональным преобладанием, т.е. к таким, для которых

.

Если матрица исходной системы (2.1) разложена в произведение треугольных и. , то, значит, вместо (2.1а) можно записать эквивалентное (2.1) уравнение

.

Введя вектор вспомогательных переменных , последнее можно переписать в виде системы

.

Таким образом, решение данной системы с квадратной матрицей коэффициентов свелось к последовательному решению двух систем с треугольными матрицами коэффициентов.

Получим сначала формулы для вычисления элементов вспомогательного вектора . Для этого запишем уравнение в развернутом виде:

(2.9)

Очевидно, все могут быть последовательно найдены при по формуле

. (2.10)

Развернем теперь векторно-матричное уравнение :

(2.11)

Отсюда значения неизвестных находятся в обратном порядке, т.е. при по формуле

. (2.12)

Итак, решение СЛАУ посредством -факторизации сводится к организации вычислений по четырем формулам: совокупности формул (2.7)–(2.8) для получения матрицы ненулевых и неединичных элементов матриц для и , формулы (2.10) для получения вектора свободных членов треугольной системы (2.11) и формулы (2.12), генерирующей решение исходной системы (2.1).

Пример 2.2. Решить СЛАУ при помощи -разложения:

Решение. Матрица системы:

.

Пользуясь формулами (2.7)–(2.8), находим

Получили:

Проверим правильность наших вычислений:

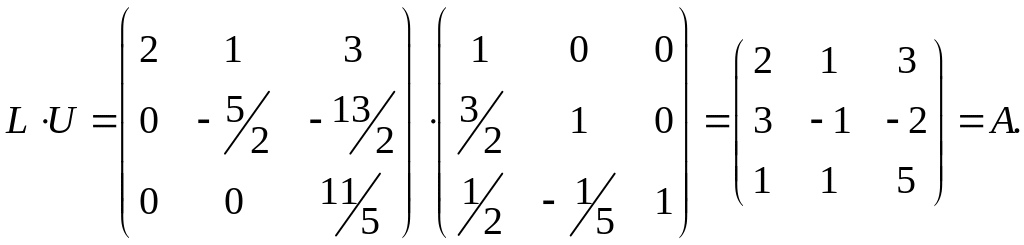
Пользуясь формулой (2.10), находим вектор вспомогательных переменных :

Теперь по формулам (2.12) находим решение исходной системы:

Решение исходной системы: .