V.4. Приближение методом наименьших квадратов

До сих пор рассматривалась интерполяция, т. е. такой способ приближения, когда значения приближаемой и приближающей функций совпадают в узлах некоторой сетки. Однако достаточно часто, например, при аппроксимации большого числа экспериментальных точек, найденных с некоторой погрешностью, интерполяция становится неразумной. В этом случае целесообразно строить приближающую функцию таким образом, чтобы сгладить влияние погрешности измерения и числа точек эксперимента. Такое сглаживание реализуется при построении приближающей функции по методу наименьших квадратов. Вид приближающей функции может быть произвольным, далее рассмотрен случай, когда приближающая функция является многочленом. При этом добиваются минимизации суммы квадратов отклонений значений приближаемой и приближающей функций в узлах сетки. Эта сумма называется квадратичным отклонением. Пусть функция при задана таблично в узлах . Необходимо построить такой многочлен 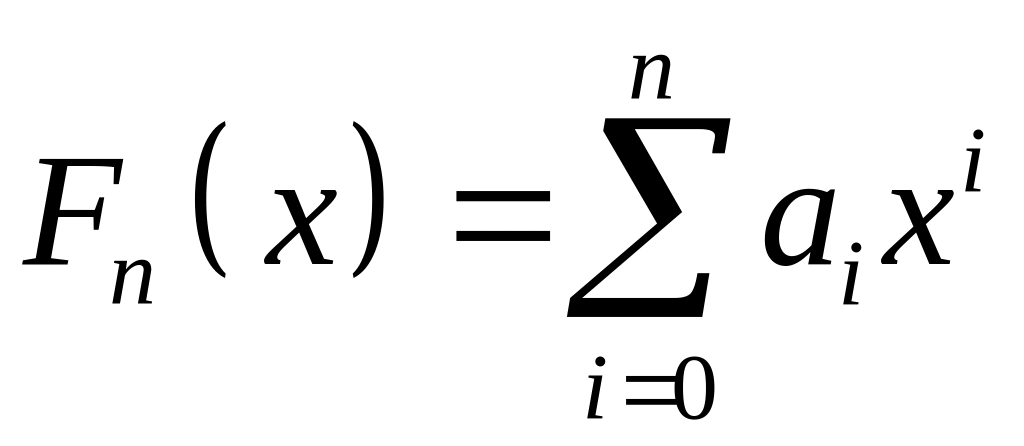, для которого минимально квадратичное отклонение

(5.17)

Очевидно, что минимума можно добиться только за счет изменения коэффициента многочлена . Необходимые условия экстремума имеют вид

(5.18)

Эту систему для удобства преобразуют к виду

(5.19)

Система (5.19) называется нормальной системой метода наименьших квадратов и представляет собой систему линейных алгебраических уравнений относительно коэффициентов . Решив систему, построим многочлен , приближающий функцию и минимизирующий квадратичное отклонение.

Метод наименьших квадратов широко применяется для сглаживания экспериментальных кривых, полученных с некоторой погрешностью. Если степень аппроксимирующего многочлена равна числу точек, то среднеквадратичный многочлен совпадает с интерполяционным. Поэтому хорошее сглаживание будет при . Но если очень мало, то для описания сложной кривой коэффициентов может не хватить. Чтобы выбрать оптимальную степень многочлена, строят многочлен по методу наименьших квадратов некоторой степени , вычисляют квадратичное отклонение и сравнивают его с известной величиной погрешности .

Если , т. е. математическая ошибка существенно превышает ошибку экспериментальных данных, то степень приближающего многочлена недостаточна для описания кривой. Если же , то старшие коэффициенты аппроксимации физически недостоверны. Хорошее сглаживание получается в том случае, когда . В этом случае степень приближающего многочлена оптимальна. Обычно начинают построение приближающего многочлена для случая и увеличивают его степень до тех пор, пока отклонение не станет примерно равным . Если при этом , то приближающий многочлен выбран верно. Если это условие не соблюдается, то следует поискать более удачный вид приближающей функции.

Можно показать методами теории вероятностей, что функция , найденная по формулам (5.18)–(5.19), с наибольшим правдоподобием совпадает с оценкой математического ожидания для заданной выборки , т.е. метод наименьших квадратов обладает сглаживающими свойствами.

Пример 5.3. Аппроксимировать по методу наименьших квадратов линейной функцией исходные данные:

	1	2	3	4	5
	2	7	10	14	20

Решение. Для удобства составим вспомогательную таблицу:

№
1	1	2	1	4	2
2	2	7	4	49	14
3	3	10	9	100	30
4	4	14	16	196	56
5	5	20	25	400	100
Сумма	15	53	55	749	202

Получаем следующую систему для определения параметров линейной функции :

Ее решение: . Т.е. уравнение прямой линии, аппроксимирующей исходные данные есть

Изобразим на одном графике исходные данные и полученную прямую:

Рис. 5.3.