Векторы угловой скорости и углового ускорения твёрдого тела, вращающегося вокруг неподвижной оси:

При вращении твёрдого тела вокруг неподвижной оси задаётся:

1) Ось вращения

2) Направление вращения

3) Угловая скорость тела

- вектор угловой скорости тела.

1. Вектор направлен по оси вращения, то есть мы задали ось вращения.

2. С конца вектора наблюдается вращение твёрдого тела против хода часовой стрелки.

3. Модуль вектора :

Вектор -вектор скользящий.

Вектор углового ускорения твёрдого тела:

- проекция векторана осьОz;- единичный вектор.

;- проекция векторана осьОz;

Вектор -вектор скользящий.

Если , то движение – равноускоренное, или равнозамедленное.

Векторная формула Эйлера.

Покажем, что

V плоскости

плоскости

- векторная формула Эйлера

Ускорение точки твёрдого тела, вращающегося вокруг неподвижной оси.

- касательная составляющая ускорения точки,

- нормальная составляющая ускорения точки.

Сложное движение точки.

Основные понятия:

Имеем:

- неподвижная система координат.

- подвижная система координат.

Относительное движение точки М – движение точкиМ относительно подвижной системы координат.

Скорость и ускорение точки Мотносительно подвижной системы координатназываютотносительными.

- относительная скорость.

- относительное ускорение.

Переносное движение.

Переносное движение– движение подвижной системы координатотносительно неподвижной системы координат.

В общем случае рассматриваем движение системы координат, связанное со свободным твёрдым телом.

Движение свободного твёрдого тела рассматривается как совокупность двух движений.

Скорость и ускорениетой точки подвижной системы координат, с которой совпадает точкаМ относительно неподвижной системы координатназываютсяпереносными.

- переносная скорость точкиМ

- переносное ускорение точкиМ

Абсолютное движение точки– движение точкиМотносительно неподвижной системы координат.

- абсолютная скорость точкиМ

- абсолютное ускорение точкиМ

Теорема о сложении скоростей.

Абсолютная скорость точкиМ равна геометрической сумме её относительной и переносной скорости.

Теорема о сложении ускорений (теорема Кориолиса).

Абсолютное ускорение точки равно геометрической сумме трёх ускорений: относительного, переносного, кориолисова.

- относительное ускорение,

- переносное ускорение,

- кориолисово ускорение.

-ускорение Кориолиса.

Определение направления ускорения Кориолиса. Правило векторного произведения.

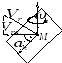
плоскости (,).

Правило Жуковского.

1. Через точку Мпровести плоскость, перпендикулярную вектору.

2. Спроецировать вектор на эту плоскость.

3. Эту проекцию в этой плоскости повернуть на угол 90° в сторону переносного вращения.

Модуль ускорения Кориолиса.

Случай равенства 0 ускорения Кориолиса:

1)

2)

3) ,т.е

ускорение Кориолиса равно 0, если вектора и- коллинеарные.

Ускорение точек плоской фигуры.

Имеем:

x₁O₁y₁ –неподвижная система координат.

Точка О– полюс плоской фигуры.

x₂Oy₂ – движущаяся поступательно система координат.

Точка М совершает сложное движение. По теореме Кориолиса:

Так как x₂Oy₂ движется поступательно, то

- ускорение полюса.

Так как x₂Oy₂ движется поступательно, то

- ускорение точки М во вращательном движении вместе с плоской фигурой относительно полюса.

- касательная составляющая ускорения точки М относительно полюса.

- нормальная составляющая ускорения точки М относительно полюса.

Ускорение любой точки плоской фигурыравно геометрической сумме ускорения полюса и ускорения точкиМво вращательном движении относительно полюса.

Расчетная схема:

Имеем:

Точка О – полюс плоской фигуры.

- ускорение полюса.

- угловая скорость полюса плоской фигуры.

- угловое ускорение полюса плоской фигуры.

ОМ в сторону дуговой стрелки.

- направлена к полюсу.