Определение главного вектора и главного момента системы сил.
Определение главного вектора и главного момента системы сил.
Спроецировав уравнение (1) на оси координат, получим:
- проекции главного вектора на оси
координат.
Главный момент системы сил относительно центра приведения.
Спроецировав уравнение (2) на оси координат, получим:
- проекции главного момента на оси
координат.
Условия и уравнения равновесия произвольной пространственной системы сил.
Условия равновесия тела.
или
Уравнения равновесия тела.
Спроецировав уравнения (3) и (4) на оси координат, получим:
- уравнения равновесия произвольной
пространственной системы сил.
Пространственная система параллельных сил.
Пространственная система параллельных сил– такая система сил, в которой линии действия сил параллельны.
Oz ||
Пространственная система сходящихся сил.
Пространственная система сходящихся сил- такая система сил, в которой линии действия сил пересекаются в одной точке.
-
равнодействующая.
Спроецировав уравнение (5) на оси координат, получим:
- уравнения равновесия пространственной системы сходящихся сил.
Произвольная плоская система сил.
Произвольная плоская система сил– такая система сил, в которой линии действия сил расположены в одной плоскости и как угодно ориентированы в ней.
Линии действия сил лежат в одной плоскости.
Ох, Оу – лежат в плоскости действия сил.
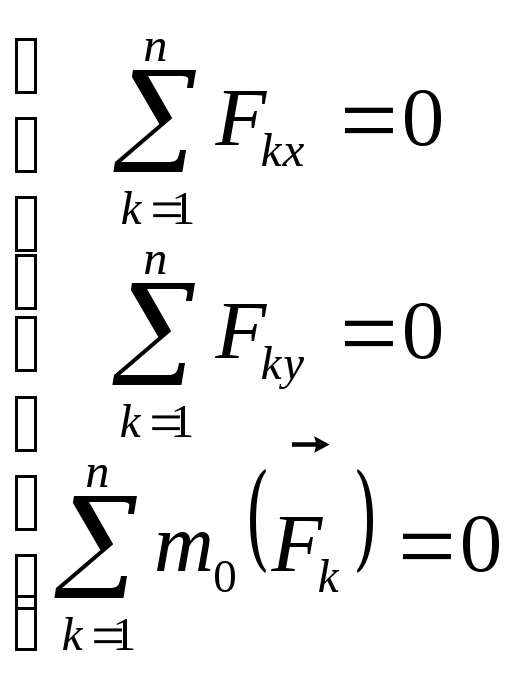
- уравнения равновесия произвольной плоской системы сил (основная форма уравнения равновесия)
ІІ форма уравнения равновесия.
a,b,c – не принадлежат одной прямой.
ІІІ форма уравнения равновесия.
Ох
не перпендикулярна АВ (α≠90°)
Статически определимые и статически неопределимые задачи.
Статически определимые задачи– такие задачи, в которых число искомых величин равно числу уравнений равновесия.
3 уравнения равновесия
3 искомых величины (
,
,
)
Статически неопределимые задачи– такие задачи, в которых число искомых величин больше числа уравнений равновесия.
3 уравнения равновесия
4 искомых величины (
,
,
,
)
Равновесие системы тел под действием произвольной плоской системы сил.
Система сил– совокупность твёрдых тел, соединённых между собой связями.
Классификация связей.
Внешние связи– связи, соединяющие тела системы с телом,не входящимв систему тел.
Шарниры А и С – внешние связи.
Внутренние связи– связи, соединяющие между собой тела системы.
Шарнир В – внутренняя связь.
Классификация сил.
Внешние силы– силы, с которыми тела, не входящие в систему тел действуют на тела системы.
Внешние силы -
,
,
,
,
,
.
Внутренние силы– силы, с которыми взаимодействуют с собой тела системы.
Внутренние силы -
,
,
,
.
,
,
Свойства внутренних сил системы тел.
геометрическая сумма внутренних сил в
системе равна нулю.
При решении задач на равновесие системы тел определяются реакции внешних и внутренних связей. Применяется метод расчленения: система тел расчленяется на отдельные тела и рассматривается равновесие каждого тела под действием заданных сил и реакций отброшенных связей.
1 метод: Рассмотрим равновесие всей системы и одного тела.
3 уравнения равновесия
4 неизвестных:
3 уравнения равновесия
2 неизвестных:
Итого: 6 уравнений равновесия
6 неизвестных
2 метод: Рассмотрим равновесие каждого тела.
3 уравнения равновесия
4 неизвестных:
,
,
,
,
3 уравнения равновесия
2 неизвестных:
,
Итого: 6 уравнений равновесия
6 неизвестных.