Момент силы относительно точки.

Момент силы относительно точки характеризует стремление силы повернуть тело относительно этой точки.

Алгебраический момент силы относительно точки– взятое с соответствующим знаком произведение модуля силы на плечо силы.

, гдеF– модуль силы,

h– плечо силы.

Векторный момент силы относительно точки.

1)- приложен в точке О;

2) - перпендикулярен плоскости треугольника ОАВ;

3) С конца вектора наблюдается стремление силы повернуть тело вокруг точки О против хода часовой стрелки.

4)

Момент силы относительно оси.

Момент силы относительно осихарактеризует стремление тела повернуться вокруг данной оси.

Порядок определения момента силы относительно оси.

1. Провести плоскость, перпендикулярную оси.

2. Спроецировать силу на эту плоскость.

3. Определить алгебраический момент проекций силы относительно точки пересечения оси и плоскости.

В случае равенства нулю момента силы относительно оси:

1) (). Ось и сила параллельны.

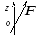
2) (h = 0). Линия действия силы пересекается с осью.

Связь между моментами силы относительно точки и оси, проходящей через эту точку.

Проекция векторного момента силы относительно точки на ось, проходящей через эту точку равна моменту силы относительно этой оси.

Пара сил.

Пара сил– совокупность двух равных по величине параллельных сил, направленных в противоположные стороны.

= Пара сил не имеет равнодействующей.

= Пару сил можно заменить только парой сил.

Действие пары сил на тело определяется следующими параметрами:

1) плоскость действия пары,

2) направление вращения пары,

3) моментом пары.

(,) – пара сил.

= -

Алгебраический момент пары сил.

Алгебраический момент пары сил– взятое с противоположным знаком произведение модуля силы пары на плечо пары.

Обозначается: mилиm(,).

, гдеF₁,F₂– модули сил пары,

d – плечо пары.

Теорема о сумме моментов сил пары относительно точки.

(смотри рис. 1)

Алгебраическая сумма моментов сил парыотносительно любой точки, лежащей в плоскости действия пары, равна алгебраическому моменту пары сил.

Теорема об эквивалентных парах.

Эквивалентные пары– две пары, лежащие в одной плоскости и имеющие равные алгебраические моменты.

Дано:

(,) и (,) – пары сил.

Если

, то

Следствия:

1. Пару сил можно как угодно перемещать и поворачивать в плоскости действия пары.

2. У пары сил можно изменять плечо и силы пары, но так, чтобы алгебраический момент пары оставался неизменным.

Пример:

Теорема о параллельном переносе пары.

Действие пары сил на тело не изменится, если пару сил перенести в плоскость, параллельную плоскости действия пары.

Плоскость I ׀׀Плоскости II

Векторный момент пары сил.

Обозначается: или(,).

1) Векторперпендикулярен плоскости действия пары.

2) С конца вектора наблюдается стремление пары повернуть тела против хода часовой стрелки.

3)

Векторный момент пары – есть вектор свободный.

Теорема о сложении двух пар, лежащих в пересекающихся плоскостях.

Дано:

и- векторные моменты пар

(,) – пара сил

Две пары, лежащие в пересекающихся плоскостях эквивалентны одной паре, векторный момент которой равен геометрической сумме векторных моментов слагаемых пар.

Сложение пар сил как угодно расположенных в пространстве.

Дано:

,, .. ,- векторные моменты пар сил.

(1) –векторный момент эквивалентной пары сил.

Спроецировав (1) на оси координат, получим:

- проекции векторного момента эквивалентной пары на оси координат.

Условие равновесия тела под действием системы пар.

=0 или =0 (2)

Спроецировав (2) на оси координат, получим:

Произвольная пространственная система сил.

Произвольная пространственная система сил– линия действия сил как угодно расположенных в пространстве.

Теорема о параллельном переносе силы.

Сила, приложенная к какой либо точке твердого тела эквивалентна такой же силе, приложенной к любой другой точке тела и паре сил, векторный момент которой равен векторному моменту силы, приложенному к начальной точке относительно новой точки приложения силы.

(,)равносильны 0,=

_(,) – пара сил

Приведение произвольной пространственной системы сил к заданному центру.

Цель приведения: замена данной системы сил другой, ей эквивалентной, но более простой.

Дано: (,,…,) – произвольная пространственная система сил

Точка О – центр приведения.

=

=

…

=

-главный вектор системы сил- геометрическая сумма сил системы.

-главный момент системы сил относительно центра приведения– геометрическая сумма векторных моментов системы сил относительно центра приведения.

Произвольная пространственная система сил эквивалентна одной силе, приложенной в центре приведения (главному вектору ) и паре сил, векторный момент которой называется главным моментом системы сил относительно центра приведения.

(,,…,)~(,)

! Главный вектор системы сил не зависит от центра приведения, а главный момент системы сил зависит от центра приведения.