
Решение задач по теоретической механике. Часть 2. Кинематика. Учебно-методическое пособие
.pdf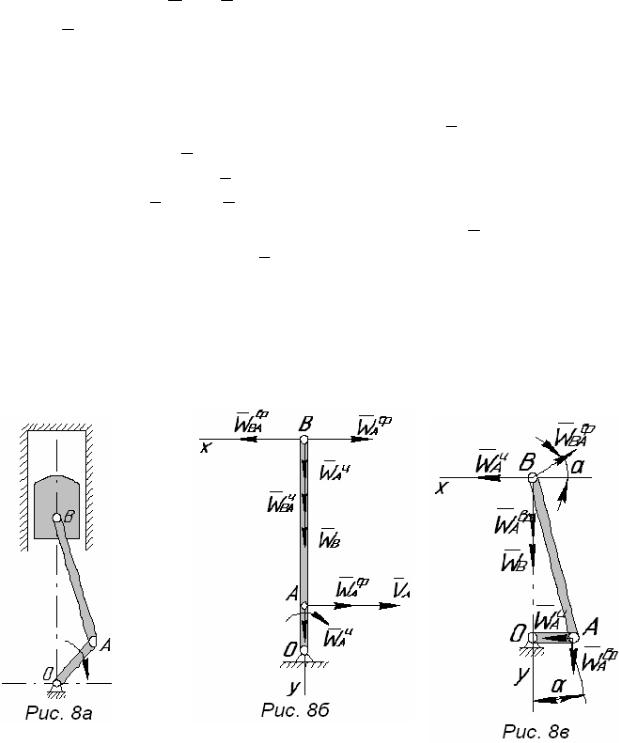
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
которой нап равл ено у скорение |
|
В , |
|
||
|
|
Е сл и |
|
п ря мая , |
п о |
w |
не |
||||||||
п ерп ендику л я рна к А В |
, то |
|
А и ω могу тбы ть заданы п роизвол ьно. |
Е сл и |
|||||||||||
ω |
|||||||||||||||
|
|
А |
А В |
|
|
|
|
|
|||||||
|
w |
, |
то задач а мож етиметь решениел ишь тол ько в том сл у ч ае, |
когда |
|||||||||||
у гол |
меж ду |
|
|
А и А В |
нету п ой и п ри нал ич ии оп редел енной зависимости |
||||||||||
|
w |
||||||||||||||
меж ду |
|
A |
и w . Д л я решения задач и тип а II сл еду етвекторноеравенство(7.1) |
||||||||||||
w |
|||||||||||||||
сп роектироватьна ось, п ерп ендику л я рну ю к w . В п равой ч астиэ тогоравенства два п ервы х вектора ( w А и wцВ А ) известны и п о вел ич ине, и п о нап равл ению . В ектор wвВрА п ерп ендику л я рен к А В , нонап равл ениеэ тоговектора неизвестно.
О но обы ч но |
у казы вается |
п редп ол ож ител ьно. |
П ри |
п роектировании (7.1) |
|||
п ол у ч им, |
таким образом, |
одно скал я рноеу равнение, |
из которого находится |
||||
вел ич ина |
|
|
врВ А . |
Е сл и э та |
вел ич ина окаж ется |
отрицател ьной, то э то бу дет |
|
|
w |
||||||
у казы ватьна то, ч топ редп ол агаемоенап равл ениевектора wврВ А п ротивоп ол ож но действител ьному . Зная wврВ А , находим ε , а п роектированием (7.1) на п ря му ю , п о которой нап равл ен вектор wВ , находим вел ич ину и нап равл ение(п о знаку п роекции) вектора wВ . Зная wА , ω и ε , мож ноп о(7.1) оп редел итьу скорение л ю бой точ ки С . П риэ том сл еду етиметьв виду , ч товектор wврСА ориентирован п оотношению к A такж е, каки wврВ А .
Задача 10. Кол енч аты й вал (рис. 8а) вращ ается с у гл овой скоростью ω0 и
у гл овы м у скорением ε 0 . О п редел итьу скорениеп оршня B иу гл овоеу скорение шату на AB п ри крайнем верхнем и крайнем п равом п ол ож ения х моты л я OA , есл идл ина моты л я r ,а дл ина шату на l .
Р еш

22
ение.
В еду щ им звеном механизма я вл я ется моты л ь ОА . Д виж ениеего задано. О п редел им скорость, иу скорениеточ киА . И меем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
цA + |
|
|
вAр , wгде |
|
цA = ω02r , |
|
|
|
врA |
= ε0r |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
ϑA = ω0r |
|
|
|
|
|
A = |
|
|
|
|
|
|
|
w |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
w |
w |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Н ап равл ения |
э тих векторов дл я |
|
|
п ервого п ол ож ения |
механизма у казаны на |
|
||||||||||||||||||||||||||||||||||||||||||
рис. 8б. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А , так как ее |
|
|||||||
|
|
Рассмотрим движ ениешату на А В . За п ол ю с п римем точ ку |
|
|||||||||||||||||||||||||||||||||||||||||||||||
скоростьиу скорениеизвестны . П о(7.1) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ц |
|
|
|
|
|
вр |
|
|
|
ц |
|
|
|
вр |
|
|
ц |
|
|
|
|
вр |
|
|
+ w |
= w |
+=w(f) + w |
w |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
BAB |
|
|
|
|
BA |
|
|
|
A |
|
|
A |
|
|
BA + wBA + w |
|
||||||||||||||||||||||||
п рич ем п о(7.2) и(7.3) |
|
= ω l× ; |
|
|
|
|
|
AB |
|
|
|
|
BA |
ε |
|
|
==wε l × |
AB |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
BA |
ω |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
где |
и |
|
|
ц |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вр |
|
|
|
|
|
|
|
|
|
|
||||||||||||
ε |
- у гл овая скоростьиу гл овоеу скорениешату на AB . |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
цBA |
|
нап равл ен от точ ки В |
|
|
|
|
|
|
вектор |
|
вBAр |
|
|||||||||||||||||||||||||||||||||
|
|
В ектор |
|
w |
|
|
|
к п ол ю су |
|
А , |
а |
w |
|
|||||||||||||||||||||||||||||||||||||
п ерп ендику л я рно А В . |
|
Н ап равим его п редп ол ож ител ьно так, |
как п оказано на |
|
||||||||||||||||||||||||||||||||||||||||||||||
рис. 8б Т ак как мгновенны й центр скоростей шатуна в |
рассматриваемом |
|
||||||||||||||||||||||||||||||||||||||||||||||||
п ол ож ениимеханизма находится в точ кеВ , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω = |
|
υA |
|
= |
ω0r |
|
|
|
|
|
|
|
|
|
|
(g) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Ф орму л а (g) оп редел я ету гл ову ю |
скоростьшату на тол ько в данны й момент |
|
||||||||||||||||||||||||||||||||||||||||||||||
времени, соответству ю щ ий рассматриваемому п ол ож ению |
механизма, п оэ тому |
|
||||||||||||||||||||||||||||||||||||||||||||||||
ε немож етбы тьп ол у ч енодиф ф еренцированием п овремени ω, |
найденногоиз |
|
||||||||||||||||||||||||||||||||||||||||||||||||
(g). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Д л я |
|
оп редел ения |
е восп ол ьзу емся |
|
тем, |
ч то л иния |
действия |
искомого |
|
|||||||||||||||||||||||||||||||||||||||
у скорения точ ки B известна: |
|
B нап равл еноп оп ря мой OB . |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
w |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
П оэ тому , п роектиру я векторноеравенство ( f ) на ось Bx , |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
B , п ол у ч им |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
п ерп ендику л я рну ю нап равл ению |
|
w |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
w |
вр |
+ w= - =w |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вр |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
BA |
|
Bx |
|
|
|
|
|
|
|||
О тсю да
wBAвр = ε0r
и, сл едовател ьно,
ε= εl0 r
Таккак wBAвр > 0 , топ редп ол ож ениеонап равл енииэ тоговектора верно.
П роектиру я равенство ( f ) на ось By , найдем п роекцию у скорения точ ки
В на э ту ось |
цA |
wwBAц By |
wω02 + |
r |
) =(=1 + |
|
|||||
|
|
|
|
l |
|

23
Т ак как wBy > 0 , то вектор wB нап равл ен в сторону п ол ож ител ьного нап равл ения оси By .
В ел ич ина у скорения точ ки B в п ервом п ол ож ениимеханизма будет
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wB |
= ω02 |
+ |
|
r |
) |
(1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рассмотрим теп ерькрайнееп равоеп ол ож ениемоты л я (рис. 8в). О братимся |
|||||||||||||||||||||||||||||||||||||||||||||||
снова к равенству |
( f ) . Т ак как п ерп ендику л я ры |
к скоростя м точ ек A и В |
|||||||||||||||||||||||||||||||||||||||||||||
п арал л ел ьны , |
|
|
|
|
|
|
то |
у гл овая |
|
скорость ω |
|
ш ату на |
|
AB |
|
равна ну л ю и, |
|||||||||||||||||||||||||||||||
сл едовател ьно, |
wBAц = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
У скорение |
|
|
|
|
|
|
врBA = 0 , |
|
п ерп ендику л я рное AB , |
п редп ол ож ител ьно нап равим |
|||||||||||||||||||||||||||||||||||||
w |
|||||||||||||||||||||||||||||||||||||||||||||||
так, как п оказанона рису нке. П роектиру я |
|
( f ) на ось Bx , пол у ч им |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 wц −=wвр |
=cosw α |
|
|
|
|
|
|
|
|||||||||||||
отсю да |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
BA |
|
Bx |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω02 r |
|
|
|
|
|
|
|
ω02 r |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε = |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l cosα |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l 2 − r 2 |
|
|
|
|
|
|
|
|||||||||||||
Т ак как wBAвр > 0 , топ редп ол ож ениеонап равл ении |
|
врBA верно. П роектиру я |
|||||||||||||||||||||||||||||||||||||||||||||
w |
|||||||||||||||||||||||||||||||||||||||||||||||
( f ) на осьBy, имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вр |
|
вр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
2r2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
BABy sinα |
|
ε0r − |
|
|
|
0= |
|
|
|
=w −w |
|||||||||||||
|
|
|
|
|
|
|
|
|
ω02 r |
|
|
|
|
|
|
|
|
|
l2 |
− r2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Е сл и |
ε 0 > |
|
|
|
|
, то wBy > 0 |
, тоестьв э том сл у ч аеwB |
|
нап равл еновниз. |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
l 2 |
|
− r 2 |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
В ел ич ина у скорения |
w |
B |
бу дет |
|
|
|
|
|
|
|
ω02 r |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wB = r(ε 0 |
− |
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l 2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− r 2 |
|
|
|
|
|
|
|
|||||||
В рассматриваемы й момент п оршень |
движ ется |
|
у скоренно вниз, |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
и |
|
|
|
|
B совп адаю тп онап равл ению . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
так как |
w |
B |
υ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω02 r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Е сл и |
|
|
ε 0 |
< |
|
|
|
|
|
|
|
|
|
|
то wB |
|
нап равл еновверхип овел ич инебу детравно |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
l 2 |
− r 2 |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
wB = r( |
|
|
ω02r |
|
|
|
|
|
|
− ε0 ) |
|
В э том сл у ч аеп оршеньдвиж ется вниззамедл енно, так |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
l2 − r2 |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
как wB и υ B имею тп ротивоп ол ож ны енап равл ения .

Задачи |
ти па III. В н ек о т о р ы й |
24 |
|
|
|
|
|
м о м |
ен т |
вр ем ен и |
извест н ы |
||||
вел ичин ы |
и н апр авл ен ия уск о р ен ий |
двух |
т о чек |
А и В |
пл о ск о й фигур ы . |
||
Опр едел ит |
ь в эт о т |
м о м ен т м гн о вен н ую |
угл о вую |
ск о р о ст |
ь |
ω , м гн о вен н о е |
|
угл о во е уск о р ен ие ε |
и уск о р ен ие л ю бо й т о чк и С. |
|
|
|
|||
Задач и э того тип а разрешимы тол ько в том сл у ч ае, когда у гол меж ду
векторами BA и разностью wB − wA нея вл я ется ту п ы м. Решениезадач и осу щ ествл я ю тп у тем п роектирования (7.10) на двевзаимноп ерп ендику л я рны е
оси (л у ч ш евсего на ось, нап равл енну ю п о AB , и на ось, |
п ерп ендику л я рну ю |
||||||||||
AB ). И зп ол уч енны хп ри п роектировании дву х скал я рны х у равнений находя т |
|||||||||||
неизвестны евел ич ины |
wвр |
wц |
|
|
|
ε |
и |
ω |
. П риэ том |
||
BA и |
BA , изкоторы хоп редел я ю т |
|
|||||||||
вел ич ина |
wц |
|
|
|
|
|
|
|
|
|
wвр |
BA мож етбы тьтол ько п ол ож ител ьной, в то время как знак |
BA |
||||||||||
|
вектора |
|
вBAр |
|
|||||||
зависитотп редп ол ож ител ьного нап равл ения |
w |
, так как известна |
|||||||||
л иш ьп ря мая , п окоторой нап равл ен э тотвектор. |
|
|
|
|
|
||||||
Задача 11. П ол зу ны |
А и В , |
соединенны естерж нем дл иной, |
движ у тся вдол ь |
||||||||
нап равл я ю щ их, которы е образу ю т меж ду |
собой у гол |
60° |
(рис. 9, а). |
||||||||
О п редел итьу скорениесередины C стерж ня в момент, когда |
|
= OB , есл иOA |
|||||||||
известно, |
ч тов э тотмоменту скорения точ ек А иВ имею твел ич ины |
|
|||||||||
|
|
wA = 3w , wB = w |
|
|
|
|
|
|
|
|
|
ип оказанны ена рис. нап равл ения .
|
|
Р еш ение. |
У сл овия |
разрешимости задач и |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
вы п ол нены . |
|
Д л я оп редел ения |
у скорения |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
точ киC п оф орму л е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CACц + |
|
CAвр+w |
|
w |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
=w |
|
|
|
(h) |
|
|
|
|
|
|
|
|
|||||||||||
необходимо знать у гл ову ю |
скорость ω |
и |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
у гл овоеу скорениеε стерж ня . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
Э ти вел ич ины найдём из соотношения |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
меж ду у скорения миточ екA иB: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
BABц + |
|
|
|
w |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где |
|
|
|
|
=wBAвр+,w |
|
|
|
|
|
(i) |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
wврBA = ε × AB , |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
wц BA =ω2 × AB, |
вр |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
п рич ём |
|
|
|
BAц |
|
нап равл еноотВ к А, а |
w |
В А |
|
|
|
|
|
|
|
|
||||||||||||||||||||
w |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
п ерп ендику л я рно к BA и п редп ол ож ител ьно нап равл ено так, как п оказано на |
||||||||||||||||||||||||||||||||||||
рис. 9,а. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
П роектиру я (i) на вы бранны еосиBx иBy, п ол у ч им два скал я рны хуравнения |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
+w−wcosBA |
|
− =w 60 |
o |
cos |
|
o |
|
|
вр |
= − w 30 cos |
|||||
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
o |
|
|
|
30 |
+wwcos |
||||||||||||
|
|
|
|
B |
|
|
|
|
|
A |
|
|
ц |
|
|
|
В |
|
|
|
A |
|
|
|
BA |
|
||||||||||
О тсю да |
wц |
BA = |
wA − wB |
=ω |
; |
w |
вр = wB + wA |
|
= ω |
|
, 33 2 |
|
||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
В А |
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||

|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wврBA |
= |
|
2ω |
|
|
. |
|
|
|
||||||||
|
|
|
|
|
|
wBAц |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ε = |
3 |
|
|
|
|||||||||||||||||
сл едовател ьно, |
ω = |
= |
ω |
; |
|
|
|
|||||||||||||||||||||||||
l |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
AB |
l |
l |
|
|
|
|
|
|
|
|||||||||||
Т ак какε > 0, то |
|
В А |
вр нап равл енов действител ьноститак, каку казанона |
|||||||||||||||||||||||||||||
w |
||||||||||||||||||||||||||||||||
рису нке. Заметим, ч товектор |
|
В А |
вр |
«стремится » вращ атьф игу ру вокру г |
||||||||||||||||||||||||||||
w |
||||||||||||||||||||||||||||||||
п ол ю са А п одвиж ению ч асовой стрел ки. |
|
|
|
|
|
|
|
|
|
ω;× w âð |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
w ц |
ω2 AC= |
ε AC==ω |
|
|
||||||||||||||||
О братимся кф орму л е(h). И меем |
×3. |
|||||||||||||||||||||||||||||||
CA |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
CA |
|
|
|
|||||||||||||||
|
|
CAц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нап равл ен отС кА , а вектор |
|
|
CAвр нап равл ен |
|||||||||||||||||||||||||||
В ектор |
w |
w |
||||||||||||||||||||||||||||||
п ерп ендику л я рнокАС так, ч тобы |
он, какивектор |
|
BAвр , «стремил ся » вращ ать |
|||||||||||||||||||||||||||||
w |
||||||||||||||||||||||||||||||||
ф игу ру вокру г п ол ю са А п одвиж ению ч асовой стрел ки(рис. 9,б). |
|
|
|
|||||||||||||||||||||||||||||
Д л я нахож дения wC п роектиру ем равенство(h) на осиBx иBy. |
||||||||||||||||||||||||||||||||
И меем |
|
|
|
|
|
o |
w |
ц |
w-ω=; w + |
|
Cx |
60= - |
cos |
|||||||||||||||||||
|
|
|
|
|
|
|
CA |
|
|
|
|
|
|
|
A |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
o |
|
вр |
3 |
|
|
|
|
= − |
|
|
|
|||||||||||||
|
|
|
|
|
A |
30Cy |
wcosCAw − = |
w . + |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w =ω |
7 |
. |
|
|
|
|
|
|
|
|
||||||||||
|
В ел ич ина у скорения |
|
|
wC |
|
равна |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
C |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Задачи |
ти па IV. |
|
В н ек о т |
о р ы й м о м ен т |
вр ем |
ен и |
извест |
н ы м |
гн о вен н ая |
||||||||||||||||||||||||||||||||
угл о вая |
ск о р о ст |
ь пл о ск о й фигур ы |
I, |
|
вел ичин а |
и н апр авл ен ие |
уск о р ен ия |
|||||||||||||||||||||||||||||||||||
к ак о й-л ибо |
её т |
о чк и А. |
Нек о т о р ая т |
|
о чк а |
В эт |
о й |
фигур ы |
о дн о вр ем ен н о |
|||||||||||||||||||||||||||||||||
пр ин адл еж ит |
и др уго й фигур е II, движ ущейся в т о й ж е пл о ск о ст и. Пр и |
|||||||||||||||||||||||||||||||||||||||||
эт о м |
уск о р ен ие т |
о чк и |
О |
и м гн о вен н ая |
угл о вая |
ск о р о ст ь |
фигур ы II |
|||||||||||||||||||||||||||||||||||
извест |
н ы |
(в |
част |
н о ст |
|
|
и, |
т |
о чк а |
О м о ж ет |
бы т ь и |
н епо движ н о й). |
||||||||||||||||||||||||||||||
Опр едел ит |
ь угл о во е уск о р ен ие фигур ы I и уск о р ен ие т |
о чк и В. |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
Д л я |
решения |
|
задач и данного тип а сл еду етсогл асно (7.10) нап исать |
|||||||||||||||||||||||||||||||||||
вы раж ениедл я у скорения точ ки B как точ ки, п ринадл еж ащ ей каж дой п л оской |
||||||||||||||||||||||||||||||||||||||||||
ф игу рев отдел ьности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ц |
|
|
|
|
|
вр |
ü |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
А |
|
|
|
|
В А |
+=w В А +;ïw w |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ц |
|
|
|
|
|
вр |
ý |
|
|
|
|
|
|
(j) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
|
|
0 |
|
|
|
|
|
В О |
+ w= В О+. w w |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
þ |
|
|
|
|
|
|
|
|
|
|
|
П риравнивая п равы еч астиэ тихравенств, п ол у ч им векторное |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A , |
|
O , |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
инап равл ения векторов |
|
w |
||||||||||
у равнение, в котором известны |
|
вел ич ины |
|
w |
||||||||||||||||||||||||||||||||||||||
|
|
ц |
BA и |
|
ц |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
w |
w |
BO (таккакизвестны |
у гл овы ескоростиотдел ьны хф игу р). |
||||||||||||||||||||||||||||||||||||||
Н еизвестны мия вл я ю тся вел ич ины |
|
wвр BA и wвр BO , п ря мы еж еп окоторы м |
||||||||||||||||||||||||||||||||||||||||
нап равл ены |
векторы |
|
|
вр |
BA и |
|
вр |
|
|
, известны . П роектиру я п ол у ч енное |
||||||||||||||||||||||||||||||||
|
w |
w |
|
BO |
||||||||||||||||||||||||||||||||||||||
векторноеу равнениена вы бранны еоси, будем иметьдва скал я рны ху равнения ,

|
26 |
изкоторы хнайдём искомы е |
вел ич ины , а затем ε1 иε2. Д л я |
оп редел ения wB восп ол ьзу емся одной изф орму л (j).
Задача 12. (рис. 10). Четы рёхзвенникрасп ол ож ен в данны й моменттак, ч то звено О А занимает верхнее вертикал ьное п ол ож ение, а точ ки О , В , О 1
находя тся |
|
на одной горизонтал и. |
О п редел ить в э том |
п ол ож ении у скорение |
||||
точ ки B, |
есл и у гл овая |
скорость звена О А равна ω0 , |
его у гл овоеу скорение |
|||||
ε0 = ω 2 0 |
|
|
|
=2r; O1B= 2r |
|
|
. |
|
|
3 |
; О А=r; АВ |
3 |
|
||||
Р еш ение. |
Т ак как точ ка B п ринадл еж итшату ну |
АВ |
и звену |
O1B, то её |
|||||||||||||||||||||||||||||||||
у скорениемож етбы тьнайденодвоя ким образом: |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ц |
|
|
|
|
|
|
|
вр ü |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
B |
|
|
|
|
|
A |
|
|
|
|
|
|
|
BA +=w |
В А +w w |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ý |
|
|
|
|
|
|
(k) |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
+ |
|
BO |
ï |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
П риэ том |
|
|
|
|
|
B |
|
|
|
|
|
|
BO1 |
|
|
|
|
|
ww 1. wþ |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ц |
|
|
|
|
|
вр |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(l) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
В э тихф орму л ах |
|
|
|
|
|
|
А |
|
|
|
|
|
А |
+ ww А . w |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
wц А =rω 2; |
|
|
|
|
|
|
wврА |
= rε |
; |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||
|
|
|
wвр BA = 2rε ; |
|
|
|
|
|
ц BA ω2 |
w=2rω× 2; AB |
|
|
|
||||||||||||||||||||||||
|
|
|
|
wц BO1 = |
|
ν |
B |
2 |
|
= |
ν |
2 |
|
|
, |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
(m) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
2r |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
BO1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
где ω и ε – |
соответственно мгновенная |
|
|
|
у гл овая |
|
скорость и мгновенное |
||||||||||||||||||||||||||||||
у гл овоеу скорениешатуна. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вр В О1 - |
||||||
|
|
|
вр BA |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
У скорение |
|
|
нап равл ено |
|
|
|
п ерп ендику л я рно |
к |
АВ , |
|
w |
||||||||||||||||||||||||||
|
w |
|
|
|
|||||||||||||||||||||||||||||||||
п ерп ендику л я рно В О 1. |
П редп ол ож им, ч то э ти векторы |
нап равл ены так как |
|||||||||||||||||||||||||||||||||||
у казанона рисунке. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

27 |
|
Т ак как мгновенны й центр |
скоростей шату на АВ находится в |
точ кеО , томгновенну ю скоростьω шату |
на АВ оп редел им п оф орму л е |
Зная ω , найдём скоростьточ киВ :
ν B
ω= νOAA =ω0.
ω==ω0r×
 3, OB
3, OB
а такж е |
wц BA = 2rω20 ; wц BO1 |
= |
|
3 |
rω2 |
0. |
|
|||||||||||
|
|
|
||||||||||||||||
И з(к) и(l) имеем |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
врBO1 |
|
ц BO1 |
|
ц А |
|
вр А |
|
|
ц В А + |
|
врВ А +. w ++ w =w |
(n)w |
||||
|
|
|
|
|
|
|
w |
|||||||||||
В э том векторном равенственеизвестны вел ич ины оп редел им издву х скал я рны ху равнений, п ол уч аемы осиBx, By. И меем
wвр В О и wвр В А , которы е
1
хп роектированием (n) на
|
|
|
|
|
|
|
ц BO1 |
|
врА |
ц В А |
|
0 + wврВ А |
600w− wcos= − w |
30 |
cos |
||||||||||
|
|
|
|
|
|
|
вр |
BO1 |
|
ц |
|
ц |
|
0 |
|
вр |
0 |
|
|
60 |
|||||
|
|
|
|
|
|
|
|
|
A |
|
BA |
|
|
|
+w BA |
w−+, w30− =wcos |
|
||||||||
отсю да |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
вр |
|
|
|
|
|
2 |
wвр BO = − |
rω20. |
|
|
|
||||||
|
|
|
|
|
|
|
w |
|
|
rω |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
BA = |
|
0 ; |
5 |
31 |
|
2 |
|
|
|
|
|
|||||||
Знак«мину с п оказы вает», ч товектор wвр BO1 |
|
|
|
|
|
||||||||||||||||||||
в действител ьностинап равл ен |
|
|
|||||||||||||||||||||||
в сторону , п ротивоп ол ож ну ю у казанной на рису нке. |
|
|
|
|
|||||||||||||||||||||
Зная |
|
ц |
|
и |
|
вр В О1 , найдём вел ич ину у скорения точ киВ : |
|
|
|
||||||||||||||||
w |
BO1 |
w |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
w |
= rω20 |
|
. |
|
57 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача |
|
13. |
|
Кривошип но-шату нны й |
механизм |
совершает |
|
|
|||||||||||||||||
п л оскоп арал л ел ьноедвиж ениев п л оскости XOY. Закон вращ ения |
кривошип а |
|
|
||||||||||||||||||||||
OA известен |
|
ϕ(t) = ω ×t , |
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ω = const |
- |
у гл овая |
скорость |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
вращ ения . |
|
= |
|
|
= a , |
точABка M |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
- середина шату на.
Найти:
1.Закондвиж ения точ ки M .
2.Т раекторию точ ки M
3.Закондвиж ения п ол зу на B
4.С коростьиу скорениеточ ки
5. С коростьточ ки M дл я |
|
|
|
|
|
ч еты рёхп ол ож ений механизма |
|
|
|
||
|
π |
|
|
3π |
|
п ри: ϕ = 0 , |
ϕ = 2 , |
ϕ = π , |
ϕ = |
|
. |
2 |
|||||
6. У гл ову ю скоростьиу гл овоеу скорениезвена AB дл я у казанны хп ол ож ений

28
7. У скорениеточ ки M дл я
ϕ = 0 , ϕ = π2 , ϕ = π , ϕ = 32π .
Реш ение.
1.И зобразим п роизвол ьное п ол ож ениемеханизма, оп редел я емоеу гл ом ϕ .
О ч евидно, ч тов каж ды й момент временивы п ол неносл еду ю щ ее векторноеравенство:
|
|
= |
|
+ |
AM |
|
OA |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
(8.1) |
|
|
|
|
Зап ишем (8.1) в п роекция хна координатны еоси, п ол у ч им: |
|||||||||||||||
Ox: |
x = a cosϕ + |
a |
cosϕ |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
|
|
|
|||||||
Oy: |
y = a sinϕ − |
a |
sinϕ |
|
|
|
|
|
|||||||
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
ì |
( ) = |
3 |
ωt) |
acos(x t |
|
|
|
|
|
|
|
|
|
|
|
ï |
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
í |
|
|
(8.2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
ï |
( ) = |
ωt) |
asin( y t |
|
|
|
|
|
|
|
|
|
|
|
|
ï |
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
î |
|
|
|
|
Ф ормул а (8.2) п редставл я ю тсобой зап исьдвиж ения точ ки M . |
|||||
2. Чтобы |
найтиточ ку M необходимоискл ю ч итьвремя изф орму л (8.2) |
||||
|
ì |
2x |
= |
wt) |
cos( |
|
|
||||
|
ï |
3a |
|
|
|
И сходя из |
í |
|
|
п осл е возведём в квадрат и сл ож ения п ол у ч им |
|
ï |
2y |
= |
wt) |
||
|
ï |
|
sin( |
||
|
î a |
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
y2 |
|
|||||
у равнениеэ л л ип са |
|
|
|
|
+ |
|
|
= 1 |
(8.3) |
|||||||||
|
|
|
|
|
||||||||||||||
( |
3 |
a)2 |
( |
1 |
a)2 |
|||||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
2 |
|
|
||||||||||
|
3 |
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|||||
С п ол у ося ми |
a и |
a , таккак |
0 ≤ t |
≤ ∞ тоточ ка M бу детдвигаться п о |
||||||||||||||
|
2 |
|||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
у казанному э л л ип су п ротив ч асовой стрел ки нач ав движ ение из точ ки с |
||||||||||||||||||
координатами |
( |
3 |
a |
);0 |
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
. Т раекторией я вл я ется весьэ л л ип с. |
|
||||||||||||||
3. Т ак как п ол зу н B движ ется п онап равл я ю щ им вдол ьоси Ox, то y t = 0 .( ) |
||||||||||||||||||
Чтобы |
|
найти координату |
x п ол зу на необходимо сп роектировать на ось Ox, |
||||||||||||
сл еду ю щ ее векторноеравенство |
|
= |
|
+ |
AB |
. |
П олOAу ч им, ч OBто дл я л ю бого |
||||||||
t |
: |
B |
= |
= |
ωt) |
|
acos(x |
t x 2 ( ) |
|
B |
|||||
|
|
|
|
. С л едовател ьно, закондвиж ения точ ки |
|
||||||||||

|
|
ωt) |
29 |
ì |
= |
acos(x t 2 ( ) |
|
í |
= |
0 ( ) |
(8.4). |
îy t |
|
||
П ол зу н B совершаетгармонич ескиекол ебания окол оточ ки O . |
|||
4. Чтобы |
найти скорость точ ки B необходимо п родиф ф еренцировать п о |
||
времениф орму л у (8.4), п ол у ч им |
|||
ì |
X |
& = - υ= |
ωt) x2 ω sin(a |
í |
|
& |
|
îυY |
= y = a |
|
|
|
|
|
2 |
2== a + ωt) 2 ω sin( υυ υ |
|
x |
y |
|
В екторскоростивсегда нап равл енвдол ьOx.
Чтобы найтиу скорениеточ ки B необходимодваж ды п родиф ф еренцироватьп о времениф орму л у (8.4) п ол у ч им
ì |
|
&& |
= - = ω |
2 |
ωt)2 |
cos(aw |
x |
|
ï |
x |
|
|
|||||
í |
|
&& |
= 0 |
|
|
|
|
|
ïw |
y |
= x |
|
|
|
|
|
|
î |
|
|
|
|
|
|
|
|
|
|
|
|
ωt) 2 |
|
|
||
|
|
2 |
2 |
== ω+ |
cos(a |
ww w |
||
|
|
x |
y |
|
|
|
|
|
В ектору скорения всегданап равл енвдол ьOx, ивсегда кточ кеO.
5. И скать скорость и у скорение точ ки M мож но анал огич но 4., но рассмотрим дру гой сп особ, оп редел ив заоднои ωAB дл я у казанны хп ол ож ений.
П ри ϕ = 0 механизм бу детрасп ол ож енвдол ьосиOx (см. рис. 13)
|
|
Н айдём внач ал ескорость точ ки A , дл я у казанного п ол ож ения исходя |
из |
||||||||||||
того, ч то точ ка A п ринадл еж иткривошип у |
OA, |
которы й вращ ается вокру г |
|||||||||||||
точ ки O с п остоя нной |
у гл овой скоростью |
|
ω . |
В ел ич ина скорости равна |
|||||||||||
υ |
a |
= ω × |
= ω × a |
|
OA |
|
|
|
|
|
|
|
OA |
в |
|
|
|
|
, а нап равл ениеп оказанона рис. 13 (п ерп ендику л я рно |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
ω a=× |
|
× |
|
|
|
сторону вращ ения кривошип а), сл едовател ьно, |
υ |
a |
j |
|
|
|
|||||||||
|
|
|
|
. Т еп ерьрассмотрим |
|||||||||||
п л оскоп арал л ел ьноедвиж ениешату на AB . Д л я э тогозвена мы знаем скорость одной точ ки A (υa ) и л инию , на которой л еж итскоростьдру гой точ ки B - э то
осьOx.
Н айдём мгновенны й центр скоростей дл я данного п ол ож ения механизма. Д л я
э тоговосстановим п ерп ендику л я ры |
в точ ках A и B л иния м, на которы хл еж ат |
||||
скорости |
|
υa |
и |
||
|
|
. |
|
|
|
υb |
|
|
|
||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
B . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
П ерп ендикул я ры |
п ересекаю тся в точ ке |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
С л едовател ьно, э то иестьп ол ож ениемгновенногоцентра скоростей (М Ц С ). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Знач ит, дл я рассматриваемого сл у ч ая |
|
скорости звена таковы |
как бу дто шату н |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
AB вращ ается |
с некоторой |
у гл овой скоростью |
ωAB |
вокру г точ ки |
B |
(как |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωAB , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
неп одвиж ной |
|
|
|
оси). |
|
|
Н айдём |
|
|
так |
как |
|
|
|
wa |
|
известно, |
|
то |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
w = ω |
AB |
×OA Þ |
ω |
AB |
= |
|
|
|
wA |
= |
ω ×a |
|
= ω |
. П ол у ч им, ч тошату н вращ ается с той ж е |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
AB |
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
у гл овой скоростью , |
ч то и кривошип , |
|
но в обратну ю |
сторону . С коростьточ ки |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
M оп редел им из равенства |
w ω |
|
|
BM ω |
a |
= |
|
w×a |
== |
|
|
× |
|
|
раз |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
M |
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
. |
|
Д ействител ьно, |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
точ ка M в два раза бл иж еи М Ц С (точ ки B ) то и скоростьу неё в два раза |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
меньше. Н ап равл ение |
wM |
|
п оказанона рис 14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Чтобы |
оп редел ить у скорение точ ки |
M , |
|
необходимо знать сл еду ю щ ие |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вел ич ины : у скорениеп ол ю са ( |
|
|
), так как за п ол ю с у добно вы братьименно |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
wA |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
точ ку |
A , у гл ову ю скоростьзвена AB (ωAB ) и у гл овоеу скорение(ε AB ), п осл е |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ч его |
|
восп ол ьзоваться |
|
|
|
ф орму л ой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вр |
|
A M+M |
w=цM AA) +( ww (8.3)w, |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
где |
|
|
вMр ( A) = ε AB × AM - |
|
вращ ател ьноеу скорениеточ ки M вокру г п ол ю са A , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
w |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
нап равл енноп ерп ендику л я рно AM . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
цM ( A) = ωAB2 |
× AM - |
центростремител ьноеу скорениеточ ки M п ри вращ ении |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
w |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вокру г п ол ю са A . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
О п редел им |
|
|
A |
|
|
как |
у скорение точ ки |
|
тел а |
OA |
|
|
вращ аю щ егося |
вокру г |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
w |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
неп одвиж ной оси O . |
|
|
|
|
|
|
|
|
|
вAр + |
|
цA : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = |
|
|
|
|
wwАвр = ε А О А О |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ц |
|
ω |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ц |
|
|
ω2 |
|
|
|
|
|
|
ω2 ×wa |
== |
|
|
|
|
|
× OA |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
A |
|
|
|
|
|
×i :× |
a= |
|
|
A |
|
|
w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
- w= |
OA |
|
|
|
|
|
|
|
|
|
|
|
, таккаквращ ениекривошип а |
||||||||||||||||||||||||||||||||||||||||||||||||||
равномерноенап равл енокточ кеO . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Чтобы |
оп редел итьε AB , необходимозап исатьф орму л у (8.3) дл я точ ки B - (дл я |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
неё нам |
известна л иния , |
на которой л еж иту скорение– ось Ox). А затем |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вр A BB+ |
|
|
цB AA) |
+( w |
|
|
|
w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
п ол у ч енну ю ф орму л у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w= |
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- зап исатьв п роекциина осьOy. |
||||||||||||||||||||||||||||||||||||||||||||||||||
П ол у ч им = + ε AB × AB + 0 Þ ε AB =0 0 0Þ |
|
вMр ( A) = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
цM ( A) |
|
|
|
|
ωAB MA== ω |
a× |
|
Þ |
|
цM ( A) |
|
ω |
a |
|
× |
|
= - |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
|
|
|
w |
|
i |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вр |
|
|
|
|
ц |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Т аким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2 ) |
|
|
i |
|
a |
|
|
a |
|
|
|
|
|
i (ω2 +wω ) -iωa=ww w- × × |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A MM |
M AA) |
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
||||
