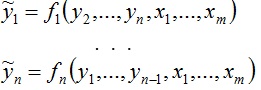- •Раздел 1. Вопрос 1. Выявление и прогноз динамики временных рядов на основе методологии Бокса-Дженкинса.
- •Вопрос 2. Методика построения и использования авторегрессионных моделей.
- •Вопрос 9. Методика построения и использования arma-моделей.
- •Вопрос 19. Методика построения и использования aRlMa-моделей. Вопрос 2. Методика построения и использования авторегрессионных моделей.
- •Понятие ar(p)- процесса.
- •Вопрос 3. Специфика моделирования многомерных динамических рядов.
- •Вопрос 4. Общая методика прогнозирования на основе эконометрических методов и моделей.
- •Вопрос 5. Задача восстановления критерия оптимальности социально-экономического объекта по нескольким принятым решениям. Вопрос 6. Способы усреднения групповой экспертной информации.
- •Вопрос 7. Прогнозирование и сглаживание временных рядов на основе алгоритмических методов.
- •Наивные методы.
- •Методы усредняющего скользящего сглаживания
- •Методы экпоненциального сглаживания
- •Вопрос 8. Выявление и прогноз динамики временных рядов на основе декомпозиционного подхода.
- •Вопрос 9. Методика построения и использования arma-моделей.
- •Вопрос 10. Эконометрическая модель и задача ее построения. Проблема идентификации систем одновременных уравнений.
- •Проблема идентифицируемости в системах одновременных уравнений
- •Вопрос 11. Методы и проблемы оценивания параметров систем одновременных уравнений.
- •Вопрос 12. Прогнозирование сезонных и циклических составляющих временных рядов, задача их построения.
- •Вопрос 13. Состав и содержание общей процедуры прогнозирования на основе методов экспертного оценивания.
- •Вопрос 14. Особенности понятия «качество прогноза» в рамках методик экспертного прогнозирования.
- •Вопрос 15. Задачи количественной обработки информации на этапе формирования групп экспертов.
- •Вопрос 16. Задача восстановления критерия оптимальности объекта хозяйствования по принятому решению.
- •Вопрос 18. Характеристики качества прогноза, методы его оценки.
- •Вопрос 19. Методика построения и использования aRlMa-моделей.
- •Вопрос 20. Состав и содержание общей процедуры социально-экономического прогнозирования.
- •Вопрос 21. Шкалы измерений и методы измерений объектов социально-экономического прогнозирования.
- •Вопрос 22. Методы уточнения спецификации статистической модели.
- •Вопрос 23. Прогнозирование и сглаживание временных рядов на основе аналитических методов.
- •Вопрос 24. Методика построения и использования оптимизационных имитационных моделей в практике прогнозирования.
- •Вопрос 25. Задачи и методы тестирования временных рядов. Состав и содержание основных тестовых гипотез.
- •Проверка наличия тенденции в среднем уровне ряда
- •Проверка наличия тенденции в дисперсии
- •Проверка на наличие автокорреляции (см. Вопрос 2.6)
- •Вопрос 6. Методы обнаружения автокорреляционных зависимостей во временных рядах.
- •Специальные тесты на проверку формы распределения случайной величины, например с помощью оценивания показателей асимметрии и эксцесса распределения
- •Вопрос 26. Понятие детерминированного и стохастического тренда. Способы тестирования и идентификации.
- •Вопрос 27. Спецификация и идентификация нелинейных связей в рамках эконометрических моделей.
- •Вопрос 28. Методы построения и прогноза моделей сезонных динамических рядов на основе индексного подхода (аддитивные индексы).
- •Вопрос 29. Методы построения и прогноза моделей сезонных динамических рядов на основе индексного подхода (мультипликативные индексы).
- •Вопрос 30. Мультиколлинеарность данных: понятие, виды, обнаружение, устранение.
- •Вопрос 31. Требования к информационному обеспечению эконометрических исследований.
- •Раздел 2. Вопрос 1. Модели с условной гетероскедастичностью. Arch, garch-модели.
- •Вопрос 2. Обоснование и использование косвенного метода наименьших квадратов.
- •Вопрос 3. Омнк. Обоснование и использование метода взвешенных наименьших квадратов.
- •Вопрос 4. Вывод формулы доверительного интервала прогноза на факторных регрессионных моделях.
- •Вопрос 5. Методы тестирования временных рядов на наличие детерминированных трендов.
- •Вопрос 6. Методы обнаружения автокорреляционных зависимостей во временных рядах.
- •Вопрос 7. Вывод формул постоптимизационного анализа (влияние изменения ссч).
- •Вопрос 8. Обоснование построения и использование критерия Дарбина-Уотсона.
- •Вопрос 9. Тесты Дики-Фуллера: назначение, процедура, интерпретация результата.
- •Вопрос 10. Информационные и прогностические критерии оценки качества эконометрических моделей прогнозирования.
- •Характеристики информационной пригодности эконометрической модели
- •Характеристики прогностической пригодности эконометрической модели
- •Вопрос 11. Обоснование задачи восстановления линейных весов частного критерия оптимальности.
- •Вопрос 12. Вывод формул постоптимизационного анализа (влияние изменения цф).
- •Вопрос 13. Вывод формулы доверительного интервала прогноза сезонной (циклической) составляющей временного ряда на основе спектрального анализа.
- •Вопрос 4. Вывод формулы доверительного интервала прогноза на факторных регрессионных моделях.
- •Вопрос 14. Методы тестирования и устранения гетероскедастичности остатков в эконометрическом моделировании.
- •Вопрос 15. Тестирование на коинтегрированность динамических рядов. Тест Дарбина-Уатсона.
- •Вопрос 16. Обоснование метода оценки компетентности экспертов на основе "задачи о лидере".
- •Вопрос 17. Понятие стационарных рядов. Тестирование на стационарность процесса.
- •Вопрос 18. Вывод формул для оценок параметров сезонных (циклических) составляющих временных рядов на основе спектрального анализа.
- •Вопрос 19. Прогнозирование на линейных моделях переменной структуры. Тест г.Чоу.
- •Вопрос 20. Прогноз времени наступления события по моде и медиане по результатам экспертного опроса.
- •Вопрос 21. Обоснование множественного критерия оценки согласованности группы экспертов.
- •Вопрос 22. Модели адаптивного прогноза. Способы коррекции параметров адаптивных моделей.
- •Вопрос 17. Принцип адаптивного прогнозирования. Оценка качества механизмов адаптации. Вопрос 23. Задача корректного формирования группы экспертов на основе результатов их прошлых экспертиз.
- •Вопрос 24. Методы оценки альтернатив на этапе обоснования экспертного выбора.
- •Вопрос 25. Оценка качества экспертного обоснования прогноза на основе парного критерия согласованности Спирмэна: обоснование, свойства, применение.
- •Вопрос 26. Оценка качества экспертного обоснования прогноза на основе парного критерия согласованности Кенделла: обоснование, свойства, применение.
- •Вопрос 27. Оценка качества экспертного обоснования прогноза на основе множественного критерия согласованности Кенделла: обоснование, свойства, применение.
- •Вопрос 28. Тест Гренжера на причинность: назначение, процедура, интерпретация результата.
- •Вопрос 29. Тест Лагранжа: назначение, процедура, интерпретация результата.
- •Вопрос 30. Тесты на гетероскедастичность: назначение, процедуры, интерпретация результатов.
- •Вопрос 31. Тестирование на однородность выборочных данных.
Вопрос 10. Эконометрическая модель и задача ее построения. Проблема идентификации систем одновременных уравнений.
Эконометрические модели в специальном их понимании являются системами одновременных уравнений и представляют собой результат статистического оценивания параметров системы математических соотношений, которые характеризуют определенную экономическую концепцию либо некоторое представление исследователя о взаимосвязи явлений и процессов в рамках изучаемой эмпирической системы. В СОУ могут входить регрессии и более специфические выражения, описывающие тренды отдельных переменных, и тождества, связывающие некоторые переменные.
Все переменные делятся на эндогенные и экзогенные переменные.
Экзогенные переменные — это переменные, задаваемые автономно, вне модели. Предопределенные переменные представляют собой всю совокупность экзогенных переменных и лаговых эндогенных переменных модели.
Эндогенные — это такие переменные, значения которых определяются внутри изучаемой системы в процессе ее функционирования. Их уровни формируются непосредственно под воздействием экзогенных переменных, а также во взаимодействии друг с другом, т.е. под воздействием предопределенных переменных.
Таким образом, под собственно эконометрической моделью понимается система взаимообусловленных зависимостей. Часть из них носит статистический характер (поведенческие соотношения). Другая часть представляет собой систему тождеств, или балансовых соотношений модели и служит для установления соответствующих ограничений, либо пропорций между структурными элементами эконометрической модели.
Обобщенное представление эконометрической модели: |
Структурное выражение СОУ в матричной форме: |
|
|
|
|
где
Гт*ту
— матрица параметров коэффициентов
эндогенных переменных; Ат*тx
—
матрица параметров коэффициентов
предопределенных переменных; Е(p)
— вектор случайных возмущений; т
— общее количество одновременных
уравнений в системе; ту
— количество эндогенных переменных;
тх
— количество предопределенных переменных;
р —
число уравнений, содержащих случайную
составляющую, причем р
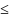 т.
т.
Проблема идентифицируемости в системах одновременных уравнений
Платой за проблему коррелируемости некоторых объясняющих переменных структурной формы эконометрической модели с модельными остатками становится порождение неопределенности в расчете параметров структурной формы системы, т.е. так называемая проблема идентифицируемости. Тип идентифицируемости уравнения системы одновременных уравнений определяется относительно возможности или невозможности вычисления структурных параметров модели через параметры ее приведенной формы.
Уравнение структурной формы эконометрической модели называется точно идентифицируемым, если все участвующие в нем неизвестные коэфф. однозначно восстанавливаются по коэффициентам приведенной формы.
Уравнение структурной формы называется сверхидентифицируемым, если все участвующие в нем неизвестные коэффициенты восстанавливаются по коэффициентам приведенной формы, причем некоторые из его коэффициентов могут принимать одновременно несколько числовых значений, соответствующих одной и той же приведенной форме. Это возможно для случая, когда коэффициентов приведенной формы больше, чем коэффициентов структурной.
Уравнение структурной формы называется неидентифицируемым, если хотя бы один из участвующих в нем неизвестных коэффициентов не может быть восстановлен по коэффициентам приведенной формы. В этом случае числа коэффициентов приведенной модели не хватает для вычисления параметров структурной формы.
Условия идентифицируемости систем:
1. Число уравнений системы должно быть равно числу анализируемых эндогенных переменных, т. е. т = ту; матрица Гт*тy должна быть невырожденной (необходимое условие).
2. Матрица наблюдений предопределенных переменных модели Х(п*тx ) должна иметь полный ранг тх, при этом, очевидно, что п >> ту + тх (необходимое условие).
3. Среди исключающих априорных ограничений не должно быть одинаковых (необходимое условие).
4. Число исключенных из i-го уравнения системы предопределенных переменных должно быть не меньше числа включенных в него эндогенных переменных, уменьшенного на единицу (необходимое условие).
5. Ранг матрицы коэффициентов приведенной формы определяется как ту — 1 (необходимое и дост. условие).
Последнее условие ввиду возможности его проверки только после оценивания приведенных коэффициентов модели часто заменяют правилом проверки свойств подматрицы исходной структурной формы модели. Уравнение считается идентифицируемым, если ранг матрицы, составленной из коэффициентов переменных, не вошедших в рассматриваемое уравнение системы, равен (больше) (ту — 1), а ее определитель не равен нулю (условие ранга). Выполнение последнего требования гарантирует выполнение всех остальных условий, обратное неверно.
На практике часто ограничиваются лишь проверкой допустимых условий идентифицируемости, в частности четвертого условия идентифицируемости, нередко называемого «условием порядка»:
Характер уравнения |
Формальное условие |
Возможность оценки |
Идентифицируемо |
EPR = IEN - 1 |
Оценка возможна с помощью КМНК, 2МНК |
Сверхидентифицируемо |
EPR > IEN - 1 |
Оценка возможна с помощью 2МНК либо других специальных методов; решение неединственно |
Неидентифицируемо |
EPR < IEN - 1 |
Оценка невозможна |
EPR — количество предопределенных переменных, не входящих в уравнение, но присутствующих в модели.
IEN — количество эндогенных переменных, включенных в уравнение.