Вопрос 28. Методы построения и прогноза моделей сезонных динамических рядов на основе индексного подхода (аддитивные индексы).
Модель временного ряда в рамках декомпозиционного подхода в аддитивной форме имеет вид:
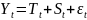, где
– трендовая составляющая;
– сезонность;
– случайная составляющая.
Индексы сезонности являются показателями, характеризующими результаты сравнения фактических уровней данного месяца или квартала с уровнями, исчисленными при выявлении основной тенденции для того же месяца или квартала.
В отличии от мультипликативных индексов, которые имеют относительную величину, аддитивные индексы отражают абсолютное отклонение каждого периода сезона от средней величины.
Общая процедура выделения сезонных составляющих для аддитивного представления:
Предварительная
оценка трендовой компоненты
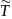временного ряда. Для этого используются
разнообразные методы сглаживания.
(Например, метод центрированного
скользящего среднего)
Выделение сезонной и случайной компонент ряда:
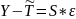
Оценка
сезонной составляющей ряда S.
Например, с помощью расчета среднего
значения по каждому периоду: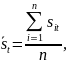
где
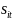– величина составляющей ряда, содержащая
сезонную составляющую t-го периода
(например, квартала) в i-ом году наблюдения;
n – количество лет наблюдения, за которое имеется статистика по t-ому периоду времени (например, кварталу).
Далее
осуществляется корректировка полученных
составляющих
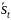так, чтобы их сумма аддитивных компонент
выходила на нуль, с помощью формулы:
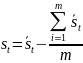
По значениям исходного ряда очищенным от сезонной составляющей (Y-S) строится аналитическая модель трендовой составляющей.
Выделение ряда случайных составляющих:
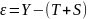
В результате получается модель , остатки которой подчинены распределению типа WN.
Точного обоснования правил оценивания интервального прогноза для метода сезонной корректировки обычно не осуществляют в силу того, что он представляет собой алгоритмическую комбинацию различных методов сглаживания рядов. В качестве весьма приблизительной оценки интервала ожидания будущего значения ряда можно принять следующее соотношение:
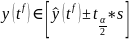
где S – стандартная ошибка полученной модели.
Вопрос 29. Методы построения и прогноза моделей сезонных динамических рядов на основе индексного подхода (мультипликативные индексы).
Мультипликативные индексы сезонности используются в случае, когда по мере повышения среднего уровня динамики увеличиваются абсолютные отклонения, вызванные сезонностью. Мультипликативные индексы сезонности отражают относительное отклонение каждого периода сезона от средней величины.
Модель временного ряда в рамках декомпозиционного подхода в мультипликативном представлении имеет вид:
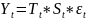, где
– тренд;
– сезонность;
– случайная составляющая.
Общая процедура выделения сезонных составляющих мультипликативным индексным методом:
Предварительная оценка трендовой компоненты (обычно здесь хорошо работают алгоритмические методы). На выходе имеем модельные значения тренда ;
Выделение сезонной и случайной компонент ряда путем деления исходного ряда Y на полученные модельные :
Таким
образом, на выходе имеем значения
;
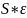Далее находим среднее значение по каждому периоду, т.е. находим
где – величина составляющей ряда, содержащая сезонную составляющую t-го периода (например, квартала) в i-ом году наблюдения;
n – количество лет наблюдения, за которое имеется статистика по t-ому периоду времени (например, кварталу).
На выходе имеем t (в случае квартальной сезонности – четыре) значения .
Далее осуществляется корректировка полученных составляющих так, чтобы их сумма выходила на количество сезонных составляющих m (в случае квартальной сезонности m=4), по формуле:
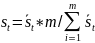
Таким образом, на выходе имеем m штук оцененных значений сезонной составляющей ряда ;
Очищение ряда от сезонной составляющей по формуле (Y/S);
По очищенным значениям строим аналитическую модель тренда (например, линейную) , получаем конкретные значения ;
Выделение ряда случайных составляющих:
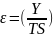
Таким образом, имеем модель , с остатками, подчиненными распределению типа WN.
Точного обоснования правил оценивания интервального прогноза для метода сезонной корректировки обычно не осуществляют в силу того, что он представляет собой алгоритмическую комбинацию различных методов сглаживания рядов. В качестве весьма приблизительной оценки интервала ожидания будущего значения ряда можно принять следующее соотношение:
где S – стандартная ошибка полученной модели.