Вопрос 16. Задача восстановления критерия оптимальности объекта хозяйствования по принятому решению.

В практике управления и прогнозирования деятельности крупных функционально и иерархически разветвленных систем особое место занимает задача определения весов частных критериев в критерии оптимальности социально-экономического объекта. Рассмотрим эту проблему в предположении о линейном характере зависимостей в дескриптивной модели планирования производственно-хозяйственной деятельности объекта.

Итак, пусть на практике в неявной форме фирмой решается следующая задача среднесрочного планирования:

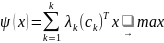
Ax=b (1)

.

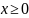При этом фирма в своих решениях руководствуется некоторой системой неявных предпочтений относительно целей своей деятельности. Формально эта система выражается структурой вектора 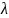. Именно эта система и важна для управляющего звена.

Для восстановления весов можно воспользоваться условиями Куна-Таккера в векторном виде. Это необходимые и достаточные условия достижения максимума целевой функции задачи (1) в точке х⁰. Для задачи (1) эти условия имеют вид:

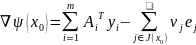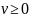, (2) ,

где 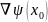- градиент функции 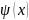в точке х⁰;

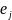– j-й единичный столбец;

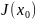- множество индексов переменных, таких, что х_j⁰=0, то есть .

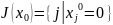Таким образом, х⁰ является оптимальным планом задачи (1) в том и только в том случае, если удастся подобрать произвольные числа y_i, где i=1,m и неотрицательные v_j, где 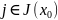, такие, что выполняется указанное векторное равенство (2). Преобразуя его и записывая в явном виде целевую функцию задачи (2), получаем следующую систему линейных уравнений:

;

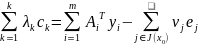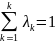; (3)

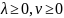
Общее решение системы (3) дает множество возможных весов , и если оно состоит из более чем одного элемента, то все допустимые наборы весов (L), входящие в него, могут использоваться для прогнозирования поведения социально-экономического объекта. Если же множество L пусто, это значит, что в формуле свертки использованы не все частные критерии или сама схема неправильно описывает систему предпочтений лица принимающего решения от имени объекта.

Вопрос 5. Задача восстановления критерия оптимальности социально-экономического объекта по нескольким принятым решениям.

Вопрос 17. Принцип адаптивного прогнозирования. Оценка качества механизмов адаптации.

Модели алгоритмического сглаживания порядков выше нулевого с наличием механизма подстройки уровней или параметров модели часто именуются адаптивными моделями, а прогнозы, построенные на из базе – адаптивными прогнозами. Модели данного вида отличаются от остальных тем, что они отражают текущие свойства ряда и способны непрерывно учитывать эволюцию изучаемого процесса, выраженную посредством динамики временного ряда.

Простейший пример:

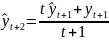
В связи с принципами формальной организации процедур подстройки параметров моделей способы адаптации можно условно разделить на алгоритмические и эвристические. Наибольшего качества в своем развитии адаптационные механизмы достигают в нейросетевых, генетических и гибридных технологиях моделирования и прогнозирования.

Последовательность процедуры адаптации моделей:

1. Определение параметров прогнозирующей модели исходя из ретроспективной информации

2. Генерация прогноза на прогнозирующей модели

3. Проверка точности прогноза (по факту события или на тестовом множестве)

4. Подстройка параметров прогнозирующей модели с помощью компенсирующего воздействия

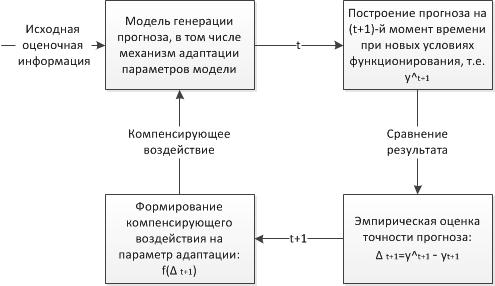
Адаптационные свойства модели заключаются в способности:

1. Своевременно выявить момент наступления изменений тенденций во временных рядах.

2. Быстро надлежащим образом модифицировать параметры модели

Требования к критериям качества прогноза:

1. Обладание достаточной чувствительностью к устойчивым изменениям тенденций

2. Минимальная реакция на случайные колебания в динамике рядов

Оценка качества адаптации:

1. Индикатор Брауна. Имеет вид: 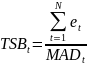где

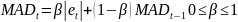
Процедура использования индикатора (или «треккинг-сигнала», TS) Брауна:

1. Задается минимальное пороговое значение

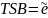
2. Проверяется соотношение между 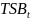и

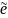
Далее, если 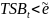– используется построенная модель, если 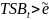– корректируется параметр 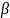модели Брауна.

Недостатки индикатора:

1. При выходе за границу, назад не обязательно возвращается, даже при нормальном режиме работы. Из-за этого необходимо контролировать во избежание ошибочных сигналов.

2. Даже если система будет давать абсолютно точный прогноз, может выйти за границу.

2. Индикатор Тригга. Имеет вид: 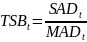где 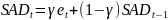– сглаженная ошибка сигнала

Индикатор TST лишен недостатков критерия Брауна и лежит в границах от -1 до 1. Крайние границы достигаются, когда ошибки постоянно имеют один знак. Обычно для практики вычислений рекомендуется подбирать параметры сглаживания γ≠β, желательно, чтобы γ<β

3. Автокорреляционный индикатор. Имеет вид: 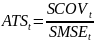где 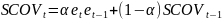– экспоненциально сглаженное значение ковариации ошибок,

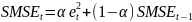
Чаще всего в основе алгоритмических способов адаптивного прогнозирования лежат следующие модели:

1. Модификации моделей экспоненциального сглаживания Брауна

2. Модификация моделей Хольта

3. Модификация моделей Хольта-Уинтерса

4. Модификация моделей сезонностей Тейла-Вейджа