ВОПРОСЫ К ЭКЗАМЕНУ по дисциплине МСЭПиЭк

РАЗДЕЛ 1. 3

Вопрос 1. Выявление и прогноз динамики временных рядов на основе методологии Бокса-Дженкинса. 3

Вопрос 2. Методика построения и использования авторегрессионных моделей. 4

Вопрос 3. Специфика моделирования многомерных динамических рядов. 6

Вопрос 4. Общая методика прогнозирования на основе эконометрических методов и моделей. 7

Вопрос 5. Задача восстановления критерия оптимальности социально-экономического объекта по нескольким принятым решениям. 8

Вопрос 6. Способы усреднения групповой экспертной информации. 9

Вопрос 7. Прогнозирование и сглаживание временных рядов на основе алгоритмических методов. 11

Вопрос 8. Выявление и прогноз динамики временных рядов на основе декомпозиционного подхода. 13

Вопрос 9. Методика построения и использования ARMA-моделей. 14

Вопрос 10. Эконометрическая модель и задача ее построения. Проблема идентификации систем одновременных уравнений. 16

Вопрос 11. Методы и проблемы оценивания параметров систем одновременных уравнений. 17

Вопрос 12. Прогнозирование сезонных и циклических составляющих временных рядов, задача их построения. 19

Вопрос 13. Состав и содержание общей процедуры прогнозирования на основе методов экспертного оценивания. 21

Вопрос 14. Особенности понятия «качество прогноза» в рамках методик экспертного прогнозирования. 22

Вопрос 15. Задачи количественной обработки информации на этапе формирования групп экспертов. 23

Вопрос 16. Задача восстановления критерия оптимальности объекта хозяйствования по принятому решению. 24

Вопрос 17. Принцип адаптивного прогнозирования. Оценка качества механизмов адаптации. 25

Вопрос 18. Характеристики качества прогноза, методы его оценки. 27

Вопрос 19. Методика построения и использования ARlMA-моделей. 28

Вопрос 20. Состав и содержание общей процедуры социально-экономического прогнозирования. 29

Вопрос 21. Шкалы измерений и методы измерений объектов социально-экономического прогнозирования. 30

Вопрос 22. Методы уточнения спецификации статистической модели. 32

Вопрос 23. Прогнозирование и сглаживание временных рядов на основе аналитических методов. 33

Вопрос 24. Методика построения и использования оптимизационных имитационных моделей в практике прогнозирования. 34

Вопрос 25. Задачи и методы тестирования временных рядов. Состав и содержание основных тестовых гипотез. 36

Вопрос 26. Понятие детерминированного и стохастического тренда. Способы тестирования и идентификации. 38

Вопрос 27. Спецификация и идентификация нелинейных связей в рамках эконометрических моделей. 40

Вопрос 28. Методы построения и прогноза моделей сезонных динамических рядов на основе индексного подхода (аддитивные индексы). 41

Вопрос 29. Методы построения и прогноза моделей сезонных динамических рядов на основе индексного подхода (мультипликативные индексы). 42

Вопрос 30. Мультиколлинеарность данных: понятие, виды, обнаружение, устранение. 43

Вопрос 31. Требования к информационному обеспечению эконометрических исследований. 44

РАЗДЕЛ 2. 45

Вопрос 1. Модели с условной гетероскедастичностью. ARCH, GARCH-модели. 45

Вопрос 2. Обоснование и использование косвенного метода наименьших квадратов. 46

Вопрос 3. ОМНК. Обоснование и использование метода взвешенных наименьших квадратов. 47

Вопрос 4. Вывод формулы доверительного интервала прогноза на факторных регрессионных моделях. 48

Вопрос 5. Методы тестирования временных рядов на наличие детерминированных трендов. 49

Вопрос 6. Методы обнаружения автокорреляционных зависимостей во временных рядах. 51

Вопрос 7. Вывод формул постоптимизационного анализа (влияние изменения ССЧ). 52

Вопрос 8. Обоснование построения и использование критерия Дарбина-Уотсона. 54

Вопрос 9. Тесты Дики-Фуллера: назначение, процедура, интерпретация результата. 55

Вопрос 10. Информационные и прогностические критерии оценки качества эконометрических моделей прогнозирования. 56

Вопрос 11. Обоснование задачи восстановления линейных весов частного критерия оптимальности. 58

Вопрос 12. Вывод формул постоптимизационного анализа (влияние изменения ЦФ). 59

Вопрос 13. Вывод формулы доверительного интервала прогноза сезонной (циклической) составляющей временного ряда на основе спектрального анализа. 60

Вопрос 14. Методы тестирования и устранения гетероскедастичности остатков в эконометрическом моделировании. 62

Вопрос 15. Тестирование на коинтегрированность динамических рядов. Тест Дарбина-Уатсона. 64

Вопрос 16. Обоснование метода оценки компетентности экспертов на основе "задачи о лидере". 66

Вопрос 17. Понятие стационарных рядов. Тестирование на стационарность процесса. 67

Вопрос 18. Вывод формул для оценок параметров сезонных (циклических) составляющих временных рядов на основе спектрального анализа. 68

Вопрос 19. Прогнозирование на линейных моделях переменной структуры. Тест Г.Чоу. 70

Вопрос 20. Прогноз времени наступления события по моде и медиане по результатам экспертного опроса. 71

Вопрос 21. Обоснование множественного критерия оценки согласованности группы экспертов. 72

Вопрос 22. Модели адаптивного прогноза. Способы коррекции параметров адаптивных моделей. 73

Вопрос 23. Задача корректного формирования группы экспертов на основе результатов их прошлых экспертиз. 74

Вопрос 24. Методы оценки альтернатив на этапе обоснования экспертного выбора. 75

Вопрос 25. Оценка качества экспертного обоснования прогноза на основе парного критерия согласованности Спирмэна: обоснование, свойства, применение. 76

Вопрос 26. Оценка качества экспертного обоснования прогноза на основе парного критерия согласованности Кенделла: обоснование, свойства, применение. 77

Вопрос 27. Оценка качества экспертного обоснования прогноза на основе множественного критерия согласованности Кенделла: обоснование, свойства, применение. 78

Вопрос 28. Тест Гренжера на причинность: назначение, процедура, интерпретация результата. 80

Вопрос 29. Тест Лагранжа: назначение, процедура, интерпретация результата. 81

Вопрос 30. Тесты на гетероскедастичность: назначение, процедуры, интерпретация результатов. 82

Вопрос 31. Тестирование на однородность выборочных данных. 84

Раздел 1. Вопрос 1. Выявление и прогноз динамики временных рядов на основе методологии Бокса-Дженкинса.

Методология Б-Д гласит, что не стоит выделять структуру ВР, поскольку вся история процесса содержится в последних наблюдениях. Таким образом, в рамках данного подхода не существует стремления выделить факторы, объясняющие сложившуюся динамику ряда, она берется за данность. Этот подход утверждает, что в динамике ряда бессмысленно отыскивать отдельные причины, у каждого процесса имеется свой собственный механизм, определяющий его специфику.

В рамках методологии Б-Д принято моделировать процессы в общем случае как смешанные или процессы общего вида.

1. Модели класса ARMA или иначе АРИСС (интегрированная модель авторегрессии и скользящей средней)

Данный класс моделей носит универсальный характер позволяет моделировать как стационарные, так и нестационарные ряды. Их часто именуют моделями общего вида, либо моделями Б-Д.

2. Модели ARMA или АРСС — модели (авторегресии и скользящей средней), которые служат для моделирования самого широкого класса стационарных процессов.

В общем случае методология Б-Д представляет собой класс итеративных процедур выделения допустимых моделей процесса в рамках общего представления класса моделей.

Общая процедура исследования динамических процессов в рамках данного подхода:

Далее можно писать все от сюда:

Вопрос 2. Методика построения и использования авторегрессионных моделей.

Вопрос 9. Методика построения и использования arma-моделей.

Вопрос 19. Методика построения и использования aRlMa-моделей. Вопрос 2. Методика построения и использования авторегрессионных моделей.

Авторегрессия – это математическая модель, в которой значение показателя выражается в виде линейной комбинации конечного числа предшествующих значений этого показателя и аддитивной случайной составляющей.

Понятие AR(1).

Модель авторегрессионного процесса первого порядка, или AR(1) имеет вид:

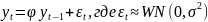
С помощью оператора сдвига модель можно записать следующим образом:

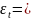L) , или

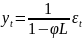
Данное представление через процесс AR является сходящимся тогда и только тогда, когда 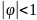, так что это условие является условием стационарности в случае AR(1)-модели.

Для процесса AR(1):

-безусловное математическое ожидание

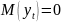
-безусловная дисперсия

.

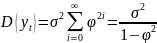
Положим, что 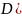)= 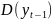, тогда

.

.

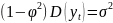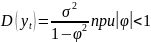-ковариация

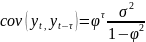
К примеру, .

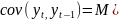Для вычисления автоковариационной функции проделаем ряд действий:

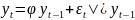
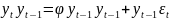
Для 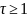возьмем мат. ожидание от обеих частей уравнения, получим

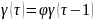– уравнения Юла-Уокера (рекуррентное выражение)¹.

Для

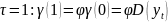
Если известно 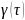для любого 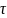, уравнение Юла-Уокера дает возможность получить

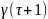
Таким образом, 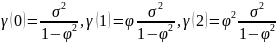и т. д.

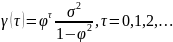
Деление левой и правой частей полученного равенства на 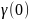дает возможность определить коэффициенты автокорреляции процесса

,

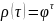Отсюда следует, что динамика ACF носит постепенно затухающий характер, что типично для AR-процессов.

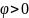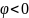В пределе, когда величина авторегрессионного сдвига стремится к бесконечности, ACF приближается к нулю. Если , ACF убывает экспоненциально. Если – то в виде колебаний, но в обоих случаях ACF убывает постепенно, а не резко. PACF имеет вид ступенчатой функции и обрывается резко.

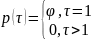
Значения PACF вычисляется как оценки последних коэффициентов в уравнении AR-процесса соответствующего порядка. Например, при AR(1) процесс PACF(1) – оценка параметра процесса автогрегрессии, и все остальные значения PACF при сдвигах, больших единицы, равны нулю.