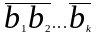11 Вопрос

Евклидово пространство

Определение: Линейное пространство Е называется евклидовым , если выполняются два требования :

1)В пространстве Е определена операция , ставящая в соответствие каждой паре элементов некоторое вещественное число – эта операция называется скалярным произведением .

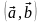2)скалярное произведение удовлетворяет следующим аксиомам.

1]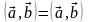 коммутативность , симметричность .

2] 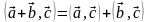дистрибутивность

3]

4] 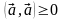причем равенство достигается только в том случае , когда 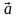нулевой.

О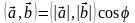 тметим , что скалярное произведение в алгебре по способу определения отличаются от скалярного произведения в геометрии, где

Свойства скалярного произведения

2)Матрица Грамма.

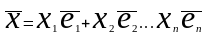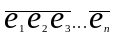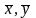
П усть - некоторый базис евклидова пространства E. Возьмём два произвольных вектора 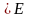. Разложим вектора по базису. Найдём представленное скалярное произведение векторов x,y в заданном базисе Е.

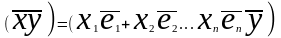= согласно аксиоме о дистрибутивности ,получим =

П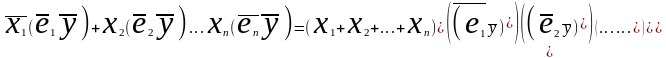 редставим элемент столбца(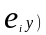 ,воспользовавшись разложением вектора y по координатам, получим( =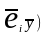

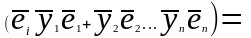
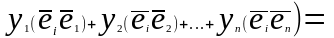
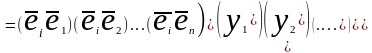
Подставляя, найдем соотношение в скалярном произведении векторов ,определим в виде матричного соотношения:

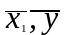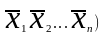
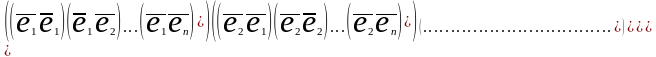=( (2)

Матрица стоящая в (2), называется матрицей Грамма. Исходя из , замечаем, что матрица Грамма симметрична относительно главной диагонали. Матрица Грамма составлена из скалярных произведений базисных векторов.

3)Изменение матрицы Грамма при переходе к новому базису.

Наряду со старым базисом 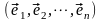, рассмотрим новый базис 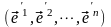. Связь между базисами устанавливается с помощью матрицы перехода Т. = Т. Матрица перехода Т, позволяет установить связь между старыми и новыми координатами.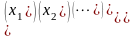 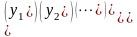(3)

Транспонируя соотношение для столбца Х. 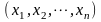= 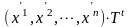(4). Подставляя выражения (3) и (4) во (2), получим: =

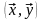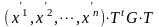
М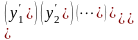 атрица Грамма в новом базисе равна: .

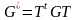Определение: два вектора называются ортогональными, если их скалярное произведение равно нулю.

Из определения ортогональности следует, что нулевой вектор ортогонален любому вектору.

Определение: система векторов называется ортогональной, если каждая пара этих векторов ортогональна между собой.

Теорема: ортогональная система не нулевых векторов, линейно независима.

Д оказательство: пусть вектора ортогональны между собой, и нулевой вектор не содержится в этой системе векторов. Составим линейную комбинацию векторов и приравняем её к нулю.

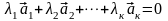(6)

Теорема будет доказана, если покажем что уравнение (6) имеет место только при нулевых коэффициентах, рассмотрим скалярное произведение вектора 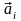из заданной системы векторов на соотношение(6).

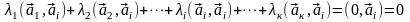
в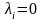 силу ортогональности системы векторов, получаем 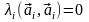, скалярный квадрат не равен нулю, следовательно.

В силу произвольности выбора , видим что все коэффициенты соотношения (6) равны нулю.

Теорема доказана.

Определение: вектор 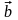называется нормированным, если его скалярный квадрат равен единице, .

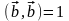Система векторов 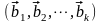называется ортонормированной, если все вектора этой системы нормированы и попарно ортогональны. В ортогональном базисе, матрица Грамма принимает наиболее простой вид.

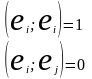i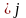 . Т.о. матрица Грамма в ортонормированном базисе.

G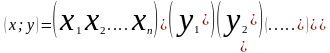 = 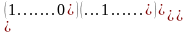единичная.

Процесс ортоганизации.

Пусть 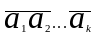-некоторая система линейно независимых векторов. Эту систему векторов можно рассматривать как базис k-мерного пространства. Установим процесс, позволяющий находить ортогональнальный базис 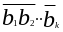.Выберем вектор 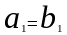.Вектор 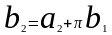при условии, что 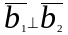(ортогональный).

Для того, чтобы найти вектор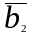 , нужно вычислить ,для этого умножим скалярно .

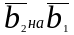Вектор 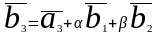.Для определения величин 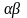,умножим

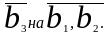
Т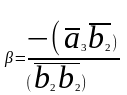 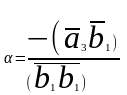огда ;

Продолжая указанный процесс, построим ортогональную систему векторов