
- •1 Вопрос
- •2 Вопрос
- •3 Вопрос
- •4 Вопрос
- •5 Вопрос
- •6 Вопрос
- •7 Вопрос
- •8 Вопрос
- •9 Вопрос
- •10 Вопрос
- •11 Вопрос
- •12 Вопрос
- •13 Вопрос
- •14 Вопрос
- •16 Вопрос
- •17 Вопрос
- •18 Вопрос
- •19 Вопрос
- •20 Вопрос
- •21 Вопрос
- •22 Вопрос
- •23 Вопрос
- •24 Вопрос
- •25 Вопрос
- •26 Вопрос
- •27 Вопрос
- •29 Вопрос
- •30 Вопрос
- •31 Вопрос
- •32 Вопрос
- •33 Вопрос
- •35 Вопрос
- •39 Вопрос
- •40 Вопрос
- •41 Вопрос
- •42 Вопрос
6 Вопрос
Комплексные числа
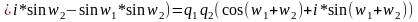
Определение: Упорядоченную пару действительных чисел x, y называют комплексным числом (x,y)
Ось абсцисс – действительная ось и обозначается Re (Real). Ось ординат – Im (Image). Комплексные числа обозначают z = x + i*y, тогда
Алгебраические операции над комплексными числами.
Суммой
двух комплексных чисел
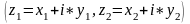 ,
является
,
является
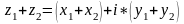 .
.
При
умножении
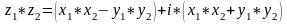
Умножение комплексных чисел легче проводить по обычным правилам раскрытия скобок с учётом, что i2 = -1
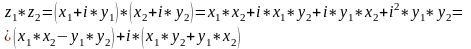
Для того, чтобы разделить два комплексных числа в алгебраической форме, необходимо умножить числитель и знаменатель этой дроби на число, сопряжённое знаменателю.
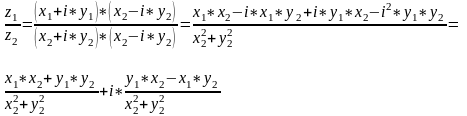
Выполним операции умножения и деления комплексных чисел в тригонометрической форме.
Пусть Z1=q1 (cosw1+i*sinw1)
Z2=q2 (cosw2+i*sinw2)
Перемножим Z1*Z2

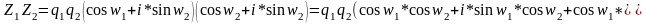 Теорема: При
умножении двух комплексных чисел в
тригонометрической форме их модули
перемножаются, а аргументы складываются.
Теорема: При
умножении двух комплексных чисел в
тригонометрической форме их модули
перемножаются, а аргументы складываются.
Разделим два комплексных числа в тригонометрической форме.
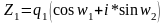
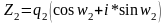
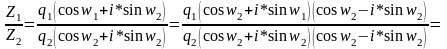
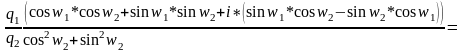
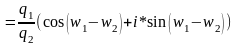
Теорема: При делении комплексных чисел в тригонометрической форме их модули делятся, а аргументы вычитаются.
Используя правила умножения комплексных чисел в тригонометрической форме легко записать формулу Муавра для возведения комплексных чисел в n-ю степень.
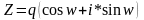
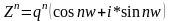
Формула Муавра легко позволяет находить корни n-ой степени из комплексного числа
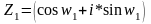 которое является
корнем n-ой
степени числа Z
которое является
корнем n-ой
степени числа Z
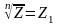
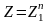
При нахождении корня n-ой степени аргумент числа Z надо записывать с учетом периода
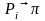
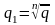
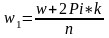
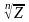 можно представить
в виде
можно представить
в виде
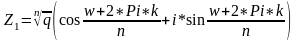
Геометрическая трактовка операций над комплексными числами.
Сложение комплексных чисел легче всего интерпретировать, используя геометрическую запись комплексного числа.
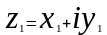
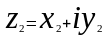
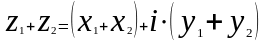
Изобразим найденное значение на координатной плоскости, сложив соответствующие координаты.
![]()
Из сделанного рисунка замечаем, что сложение комплексных чисел соответствует сложению векторов по правилу параллелограмма.
Умножение комплексных чисел иллюстрируется с помощью тригонометрической записи комплексных чисел. Пусть имеются
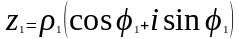
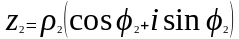
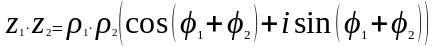
Изобразим полученные результаты на комплексной плоскости.
![]()
Для
того, чтобы изобразить произведение
двух комплексных чисел, от вектора
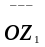 отложим угол
отложим угол
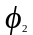 ,
затем на полученном луче откладываем
от начала координат отрезок, длина
которого равна произведению модулей.
,
затем на полученном луче откладываем
от начала координат отрезок, длина
которого равна произведению модулей.
Из полученного рисунка видим, что умножение комплексных чисел сводится к повороту с растяжением.
7 Вопрос
Линейные пространства
Определение:
Множество L
элементов
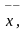
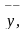
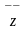 ,
… называется линейным пространством,
если выполняются следующие требования
,
… называется линейным пространством,
если выполняются следующие требования
На множестве L определена операция сложения элементов для
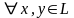
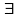
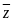
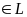
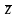 =
=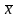 +
+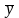
На множестве L определена операция умножения элементов на число.Для
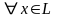
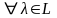
 , называемый
произведением числа
, называемый
произведением числа
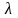 на число x
и обозначается
на число x
и обозначается
=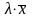 .
.
Введенные две операции удовлетворяют следующим 8 аксиомам.
1) + = + коммутативность сложения
2) ( + ) + = + ( + ) ассоциативность сложения.
3)
Существование нулевого элемента.
Существует нулевой элемент такой, что
для любого
=
+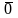
4) Существование противоположного элемента.
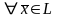
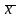 +
=
+
=
5) Для
 R
R
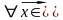 L
,
L
,
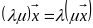 ассоциативно относительно числовых
множителей.
ассоциативно относительно числовых
множителей.
6)
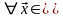 L
,
L
,
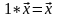
7)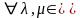 R
R
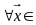 L
,
L
,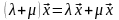 дистрибутивно
относительно сложения чисел .
дистрибутивно
относительно сложения чисел .
8)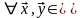 R
R
 R
,
R
,
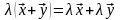 дистрибутивно относительно сложения
элементов .
дистрибутивно относительно сложения
элементов .
Линейная зависимость векторов .
Определение:
Совокупность векторов
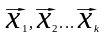 называется линейно зависимой, если
существует набор из k
чисел
называется линейно зависимой, если
существует набор из k
чисел
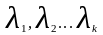 хотя бы одно из которых отлично от нуля
и линейная комбинация
хотя бы одно из которых отлично от нуля
и линейная комбинация
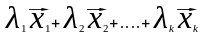 =0
(1)
=0
(1)
равна нулю.
Система векторов называется линейно независимой , если соотношение (1) возможно только при нулевых коэффициентах .
Теорема: Имеют место следующие утверждения:
Если в системе векторов
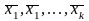 имеется линейно зависимая подсистема,
то вся система линейно зависима.
имеется линейно зависимая подсистема,
то вся система линейно зависима.Если система векторов
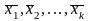 линейно независима, то всякая её
подсистема, также линейно независима.
линейно независима, то всякая её
подсистема, также линейно независима.Если система векторов
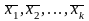 линейно зависима, то хотя бы один из
векторов этой системы является линейной
комбинацией остальных векторов.
линейно зависима, то хотя бы один из
векторов этой системы является линейной
комбинацией остальных векторов.Если в системе векторов хотя бы один из векторов является линейной комбинацией остальных, то эта система векторов линейно зависима.
Если система векторов линейно независима,
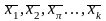 линейно
зависима, то
линейно
зависима, то
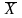 является линейной комбинацией векторов
.
является линейной комбинацией векторов
.Если система векторов линейно независима и
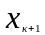 не является линейной комбинацией
векторов
,то
система
не является линейной комбинацией
векторов
,то
система
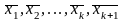 линейно независима.
линейно независима.
Доказательства:
Утверждение
1: Докажем
первое утверждение. Дана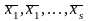 .
Предположим, для определённости, что
подсистема
линейно зависима. Это делает существуют
числа
.
Предположим, для определённости, что
подсистема
линейно зависима. Это делает существуют
числа
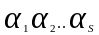 не все равные 0. При котором линейная
комбинация
не все равные 0. При котором линейная
комбинация
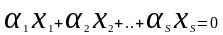 .
Запишем набор чисел
.
Запишем набор чисел
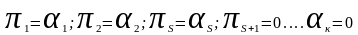
Заметим, что выписанные числа образуют линейную комбинацию
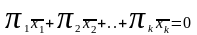
Причём
не все коэффициенты равны 0,следовательно,
что система
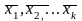 линейно
зависима.
линейно
зависима.
Утверждение 2: Непосредственно вытекает из утверждения 1.(рассуждения от противного.)
Утверждение
3: Пусть
система векторов
линейно зависима. Это означает, что
существует набор чисел
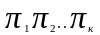 ,
хотя бы одно из которых не равно 0,и
линейная комбинация векторов с этими
числами обращаются в 0.
,
хотя бы одно из которых не равно 0,и
линейная комбинация векторов с этими
числами обращаются в 0.
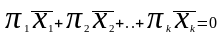 .
.
Пусть
для определённости число
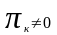 ,тогда
последнее соотношение можно представить
в виде:
,тогда
последнее соотношение можно представить
в виде:
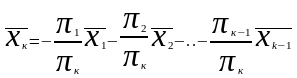
Получили, что один из векторов системы является линейной комбинацией остальных векторов.
Утверждение
4: Пусть
для определённости вектор
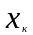 является
линейной комбинацией остальных векторов
является
линейной комбинацией остальных векторов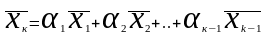
Выбрав
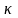 величин, равными
величин, равными
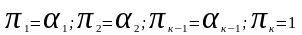 ,
получим нетривиальную линейную
комбинацию равную 0:
,
получим нетривиальную линейную
комбинацию равную 0:
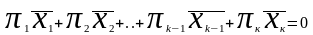 .
.
Таким образом, показали, что вектора линейно зависимы.
Утверждение
5: пусть
система векторов
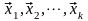 - линейно независимая, а система векторов
- линейно независимая, а система векторов
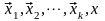 - линейно зависимая. Образуем линейную
комбинацию векторов
,
и приравниваем её к нулю.
- линейно зависимая. Образуем линейную
комбинацию векторов
,
и приравниваем её к нулю.
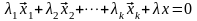 ,
так как эта система векторов линейно
зависима, то не все значения
,
так как эта система векторов линейно
зависима, то не все значения
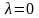 ,
заметим, что
,
заметим, что
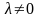 ,
так как если бы
,
то получили бы нетривиальную линейную
комбинацию векторов
,
а это не возможно в силу линейной
независимости векторов
.
Так как
,
то вектор
,
так как если бы
,
то получили бы нетривиальную линейную
комбинацию векторов
,
а это не возможно в силу линейной
независимости векторов
.
Так как
,
то вектор
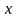 можно представить в виде
можно представить в виде
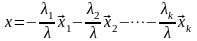 ,
то есть получим представление для
вектора
,
в виде линейной комбинации векторов
.
,
то есть получим представление для
вектора
,
в виде линейной комбинации векторов
.
Утверждение 6: непосредственно вытекает из утверждения 5.
Базис. Размерность.
Определение:
пусть V
не нулевая оболочка n-мерных
векторов. Система векторов
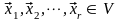 ,
называется базисом линейной оболочки,
если она линейно независима и порождает
всю оболочку V,
,
называется базисом линейной оболочки,
если она линейно независима и порождает
всю оболочку V,
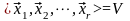 .
.
Лемма:
Пусть V
не нулевая оболочка n-мерных
векторов,
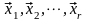 -
базис этой оболочки. Если система
векторов
-
базис этой оболочки. Если система
векторов
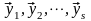 ,принадлежит
линейной оболочке V,
линейно независима, то выполняется
неравенство
,принадлежит
линейной оболочке V,
линейно независима, то выполняется
неравенство
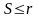 .
.
Доказательство:
Составим линейную комбинацию векторов
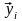 ,
и приравняем её к нулю
,
и приравняем её к нулю
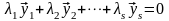 .
Разложим каждый из векторов
.
Разложим каждый из векторов
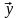 по базису X,
получим:
по базису X,
получим:
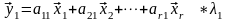
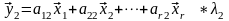
……………………………
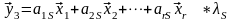
Выразим линейные комбинации y через вектора x. В результате получается:
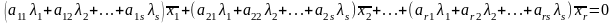
Поскольку вектора, образующие базис линейно независимы, приходим к системе линейных уравнений:
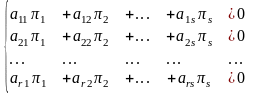
Для
доказательства леммы предположим
противное. Пусть s>r;
замечаем, что при этом система уравнений
совместно. Она обладает нулевым решением,
если s>r,
то есть число неизвестных в системе
больше числа уравнений, то эта система
неопределенная(не может быть приведена
к
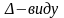 )
Таким образом заключаем, что при условии
s>r
система обладает бесконечным множеством
решений, среди которых присутствует
ненулевое решение. Таким образом
получаем противоречие. С одной стороны
система векторов y
линейно-независима, с другой стороны
существует ее тривиальное линейная
комбинация равная 0. Полученное
противоречие показывает, что этот
случай невозможен.
)
Таким образом заключаем, что при условии
s>r
система обладает бесконечным множеством
решений, среди которых присутствует
ненулевое решение. Таким образом
получаем противоречие. С одной стороны
система векторов y
линейно-независима, с другой стороны
существует ее тривиальное линейная
комбинация равная 0. Полученное
противоречие показывает, что этот
случай невозможен.
Теорема: Любая ненулевая линейная оболочка n-мерных векторов обладает конечным базисом. Число векторов, входящих в базис постоянно и не зависит от выбора базиса. Число векторов, входящих в базис, называется размерностью линейной оболочки и обозначается dimV.
Доказательство: Пусть
некоторая линейная независимая система
векторов принадлежащая оболочке V,
если эта система векторов не является
базисом, то в оболочке V
найдется вектор
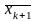 ,
который не является линейной комбинацией
векторов
.
Согласно утверждению 6 теоремы о линейной
независимости, система векторов
линейно независима. Продолжая указанный
процесс, будем увеличивать число линейно
независимых векторов. Эта процедура
не может тянуться бесконечно, поскольку
в пространстве n-мерных
векторов существует базис
,
который не является линейной комбинацией
векторов
.
Согласно утверждению 6 теоремы о линейной
независимости, система векторов
линейно независима. Продолжая указанный
процесс, будем увеличивать число линейно
независимых векторов. Эта процедура
не может тянуться бесконечно, поскольку
в пространстве n-мерных
векторов существует базис
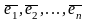 =>
процесс построения линейно независимой
системы оборвется на некотором шаге,
который ≤ n
(r≤n),
и система векторов
=>
процесс построения линейно независимой
системы оборвется на некотором шаге,
который ≤ n
(r≤n),
и система векторов
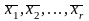 ,
образует базис оболочки V.
Покажем, что число векторов, входящих
в различные базисы, одно и тоже. Пусть
,
образует базис оболочки V.
Покажем, что число векторов, входящих
в различные базисы, одно и тоже. Пусть
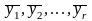 другой
базис оболочки V.
Согласно лемме, должны выполняться
только в случае, когда S≤r,
r≤S,
оба неравенства выполняются только в
случае, когда S=r
=> что число векторов входящих в базис
не зависит от выбора базиса.
другой
базис оболочки V.
Согласно лемме, должны выполняться
только в случае, когда S≤r,
r≤S,
оба неравенства выполняются только в
случае, когда S=r
=> что число векторов входящих в базис
не зависит от выбора базиса.
Определение: Рангом системы векторов называется размерность линейной оболочки, натянутой на эти вектора.
