
- •1 Вопрос
- •2 Вопрос
- •3 Вопрос
- •4 Вопрос
- •5 Вопрос
- •6 Вопрос
- •7 Вопрос
- •8 Вопрос
- •9 Вопрос
- •10 Вопрос
- •11 Вопрос
- •12 Вопрос
- •13 Вопрос
- •14 Вопрос
- •16 Вопрос
- •17 Вопрос
- •18 Вопрос
- •19 Вопрос
- •20 Вопрос
- •21 Вопрос
- •22 Вопрос
- •23 Вопрос
- •24 Вопрос
- •25 Вопрос
- •26 Вопрос
- •27 Вопрос
- •29 Вопрос
- •30 Вопрос
- •31 Вопрос
- •32 Вопрос
- •33 Вопрос
- •35 Вопрос
- •39 Вопрос
- •40 Вопрос
- •41 Вопрос
- •42 Вопрос
4 Вопрос
Правило Крамера
Лемма: Сумма произведений всех элементов некоторого столбца определителя на алгебраические дополнения соответственных элементов другого столбца равна 0.
Доказательство: Рассмотрим определитель n-го порядка
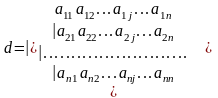
Разложим определитель по j-му столбцу.
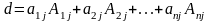
Заменим
в определителе d
по j-ому
столбцу столбцом
 ,
получим
,
получим
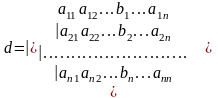
Так
же разложим определитель
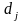 по j-ому
столбцу.
по j-ому
столбцу.

Заменив
в определителе dj
столбец
b
любым из оставшихся столбцов, получим
определитель
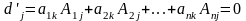
Заметим,
что определитель
 будет содержать два (
будет содержать два ( )
одинаковых столбца , поскольку k-ый
столбец мы поставили вместо j-ого
столбца.
)
одинаковых столбца , поскольку k-ый
столбец мы поставили вместо j-ого
столбца.
Согласно свойствам определителя, если в определителе содержится два одинаковых столбца, то он равен 0.
Рассмотрим определённую систему линейных уравнений n-ого порядка.
 (2)
(2)
Пусть
набор чисел
 является решением системы (2). Подставляя
величины
является решением системы (2). Подставляя
величины
 вместо неизвестных, получим систему
тождеств (3).
вместо неизвестных, получим систему
тождеств (3).
(3)
Возьмём
число j
из множества первых n
натуральных чисел. Умножим первое
тождество на
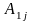 ,
второе – на
,
второе – на
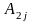 ,
… , n-ое
– на
,
… , n-ое
– на
 ,
где алгебраические дополнения вычисляются
с помощью определителя n-ого
порядка, составленного из коэффициентов
системы (2).
,
где алгебраические дополнения вычисляются
с помощью определителя n-ого
порядка, составленного из коэффициентов
системы (2).
Сложив полученные тождества, придём к выражению

Коэффициент
при
является разложением определителя
коэффициентов по j-ому
столбцу и он равен
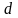 .
Остальные коэффициенты при
в левых частях равны сумме произведений
элементов некоторого столбца на
алгебраические дополнения соответствующих
элементов другого столбца.
.
Остальные коэффициенты при
в левых частях равны сумме произведений
элементов некоторого столбца на
алгебраические дополнения соответствующих
элементов другого столбца.
С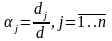 огласно
лемме, все эти коэффициенты равны 0.
Выражения, стоящие в правой части при
доказательстве леммы обозначают
.
Таким образом получили выражение Покажем
что система чисел (4) удовлетворяет
системе (2)
огласно
лемме, все эти коэффициенты равны 0.
Выражения, стоящие в правой части при
доказательстве леммы обозначают
.
Таким образом получили выражение Покажем
что система чисел (4) удовлетворяет
системе (2)

Подставим уравнение системы (2) и подставим в него значение (4)
Выражение,
стоящее в круглых скобках =0, если
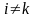 (согласно лемме) если
(согласно лемме) если
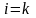 то выражение в скобках равно определителю
d.
Система (4) действительно является
решением системы (2). Получаем решение
системы называемое правилом Крамера.
то выражение в скобках равно определителю
d.
Система (4) действительно является
решением системы (2). Получаем решение
системы называемое правилом Крамера.
5 Вопрос
Основные операции над матрицами
а) Две матрицы А и В называются равными, если они имеют одинаковые размеры и если их элементы, стоящие на одинаковых местах, совпадают.
b) Суммой двух матриц А и В одних и тех же размеров называется матрица С тех же размеров, элементы которой определяются размером:
с
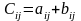 )
Произведением матрицы А на q
называется матрица С элементы которой
определяются выражением
)
Произведением матрицы А на q
называется матрица С элементы которой
определяются выражением
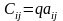 (2)
(2)
Теорема: Определитель произведения нескольких квадратных матриц равен произведению определителей.
Доказательство: В силу ассоциативности умножения матрицы достаточно рассмотреть случай произведения двух матриц, т.е. достаточно доказать, что det (AB) = det A * det B.
Выпишем вспомогательный определитель порядка 2n

Видим,
что в верхнем левом углу определителя
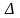 стоят элементы матрицы А.
стоят элементы матрицы А.
Стоят элементы матрицы А в правом нижнем углу определителя , стоят элементы матрицы В. Правый верхний угол определителя состоит из нулевых элементов . Левый нижний угол содержит 1 по главной диагонали и нули на остальных местах . Вычислим определитель по 1 n- строкам воспользовавшись теоремой Лапласа.
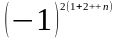 =detA
detB=detA*debB
=detA
detB=detA*debB
Преобразуем определитель , не меняя его значения .Создадим нули в правом нижнем углу определителя . При этом нули в правом верхнем углу исчезнут .
В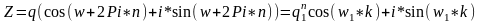 ыпишем
элемент , который при таких преобразованиях
окажется на пересечении i-той
строки (n+j)
строкой .
ыпишем
элемент , который при таких преобразованиях
окажется на пересечении i-той
строки (n+j)
строкой .
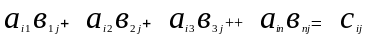
С
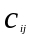 равнивая
получаем выражение с формулой (3) ,
замечаем что получаем значение
,являющегося произведением матрицы А
на В . То образуется , выполнив
преобразования определителя
.
равнивая
получаем выражение с формулой (3) ,
замечаем что получаем значение
,являющегося произведением матрицы А
на В . То образуется , выполнив
преобразования определителя
.
Вычислим определитель разложив по последующим n столбцам.
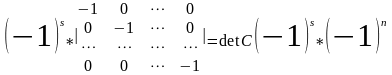
 =
detC
=
detC
Подсчитаем число 3. S = 1+2+3+4+...+n+(n+1)+(n+2)+...+2n=(1+2n/2)*2n=n+2
Воспользовавшись формулой для сумм арифметической прогрессии и определитель будет равен

Таким образом получим , что определитель матрицы C (detC)
det(C)=det(AB)=det(A)det(B)
Определение: квадратная матрица называется вырожденной (особенной) , если ее определитель (det) =0.
Следствия из теоремы.
1)Произведение квадратных матриц n – го порядка , содержащих хотя бы одну вырожденную матрицу , является вырожденной матрицей.
2)Произведение невырожденных матриц , является невырожденной матрицей.
Роль единицы при умножении матриц играет единичная матрица . Единичную матрицу обозначают E и она состоит из единиц, расположенных выражений.
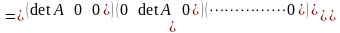 вычислим определитель
из левой и правой части записанного
вычислим определитель
из левой и правой части записанного
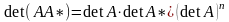 ,
таким образом замечаем, если А не
вырожденная, то присоединенная матрица
А*, также является не вырожденной,
причем:
,
таким образом замечаем, если А не
вырожденная, то присоединенная матрица
А*, также является не вырожденной,
причем: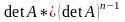 ,
аналогичный результат получается при
рассмотрении произведения
,
аналогичный результат получается при
рассмотрении произведения
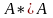 ,
заметим, что если матрица С=
,
заметим, что если матрица С=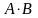 и если элементы одной из перемножаемых
матриц разделит на некоторое число, то
все элементы матрицы С разделятся на
это число. С учётом сделанного замечания
и если элементы одной из перемножаемых
матриц разделит на некоторое число, то
все элементы матрицы С разделятся на
это число. С учётом сделанного замечания
В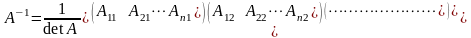 ыражение
(5) позволяет вычислить обратную матрицу.
ыражение
(5) позволяет вычислить обратную матрицу.
Решение матричных уравнений
Пусть даны две матрицы A и B, причем A-невырожденная и 2 неизвестная матрицы X, Y. С помощью обратной матрицы можно решать уравнения вида:
A*X=B (1)
Y*A=B (2)
Для решения уравнения (1) умножаем обе части на матрицу обратную к А слева

в силу ассоциативности матриц левую часть уравнения представим в виде

произведение, стоящее в скобках

умножение на ед. матрицу не изменяет матрицу Х. Чтобы Y*A=B необходимо умножить на обратную матрицу справа

в силу ассоциативности
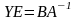
 -
решение уравнения (2)
-
решение уравнения (2)
