32 Вопрос

Равномерная непрерывность функции

Пусть функция определена на множестве , каждая точка которого является предельной.

Напомним, что точка называется предельной, если в любой ее -окрестности содержится бесконечно много точек рассматриваемого множества.

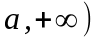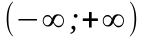Примерами такого множества Х являются: [ ] - отрезок, ( ) - интервал, [ ) - полусегмент, [ - полупрямая, - прямая.

Определение: Функция 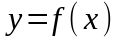называется равномерной непрерывной на множестве 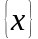, если для любого положительного числа найдется отвечающее ему положительное число такое, что для всех значений 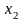, удовлетворяющих неравенству | 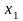- | < выполняется неравенство | - | <

Замечание1: Если функция равномерно непрерывна на множестве {x}, то она непрерывна в каждой точке x₀ множества {х}.

Для доказательства замечания1 достаточно зафиксировать т. , взяв в качестве нее произвольную точку 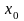( = ) из отрезка [ ]

При этом из определения равномерной непрерывности получим определение функции в т. 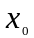по Коши.

Замечание2: Из непрерывности функции на множестве не вытекает равномерная непрерывность функции на этом множестве.

Пример. Рассмотрим функцию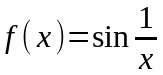 на отрезке 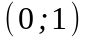. Видим, что эта функция непрерывна на этом интервале.

Заданная функция может быть представлена в виде y=sin(x) ,t=1/x обе эти функции являются элементарными и непрерывными на рассматриваемом интервале следовательно их суперпозиции .Сложная функция так же непрерывна на этом интервале . Покажем , что эта функция не является равномерно непрерывной на этом интервале .

Р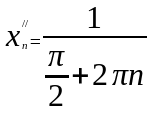 ассмотрим последовательност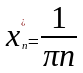и и

Видим что обе последовательности являются бесконечно малыми следовательно их разность тоже является бесконечно малой последовательностью. Таким образом для любого положительного числа δ найдутся значения n , такие что 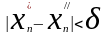.При этом соответствующие значения функции будут равны 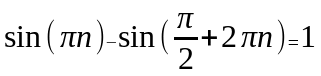для всех номеров n. Выбрав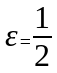 замечаем что какое бы малое значение мы не брали всегда найдутся точк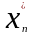и и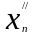 модуль разности значения функции будет равен 1> .

На интервале (0,1)функция не является равномерно непрерывной .

Докажем что функция будет равномерно непрерывной на (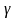 ,1) , где .

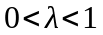Рассмотрим функцию 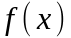на отрезке 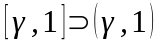и если мы покажем , что функция равномерно непрерывна на отрезке, то следовательно она равномерно непрерывна на интервале( ,1).

Рассмотрим модуль разности двух непрерывных функций

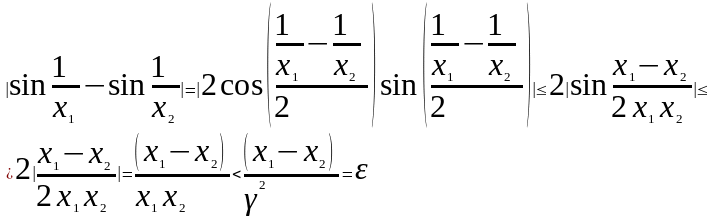
Значение 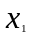, 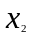положительны , то таким образом видим , что для любых положительных 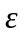найдутся значения удовлетворяющих неравенству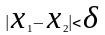 для которых будут выполнятся требования если мы в качестве δ возьмем 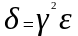.Равномерные непрерывные функции на отрезке 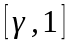следовательно равномерна непрерывна на интервале

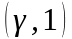
Теорема Кантора (1845-1918)

Теорема: Если непрерывна на 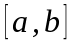, то она равномерно непрерывна на этом отрезке.