29 Вопрос

Первый замечательный предел.

Т еорема: предел функции в нуле существует и равен единице .

Доказательство: Выполним вспомогательное построение. Изобразим единичную окружность, на которой отложим угол x., круговой сектор

и треугольники СОВ, АОВ, из выполнения

построения вытекает

вместо площадей подставим соответствующие

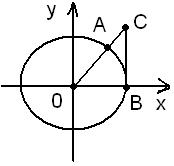выражения, получим:

, при x sin x положителен, поэтому, разделив неравенство на sin x сохраним прежние знаки:

Заметим, что функции входящие в выражение (1), следовательно, неравенство (1) остаётся справедливым и при отрицательном значении х.

Видим произвольную последовательность сходящейся к 0,на основании неравенства (1) . Предел последовательностей стоящих слева

Т аким образом, по принципу двустороннего ограничения заключаем, что , откуда на основании определения функции по Гейне вытекает, что первый замечательный предел существует:

Второй замечательный предел

Теорема: Предел функции в 0 существует и равен е.

Отметим, что функция f(x) не является элементарной. Из второго замечательного предела вытекает существование предела функции

Следствие:

30 Вопрос

Локальные и глобальные свойства непрерывных функций

Определение: Локальными свойствами функции называют свойства справедливые в некоторой видимой окрестности точки.

Определение: Глобальные свойства функции справедливы на всем множестве определения функции.

Например, чётность, нечётность, периодичность, монотонность.

Локальные свойства непрерывных функций.

Теорема о локальной ограниченности функции, имеющей конечный предел: Пусть функция f(x) определена на множестве {x} и имеет конечное предельное значение в точке а.

Тогда существует такое положительное значение , что функция f(x) является ограниченной на множестве , которое является пересечением {x} и -окрестности точки а.

Доказательство:Пусть функция f(x) имеет в точке а конечный предел, равный b.

Согласно определению предела функции по Коши, для некоторого числа ε найдётся отвечающее ему число , такое, что .

Последнее неравенство можно записать в виде .

Если функция f(a) не определена в точке а, то теорема доказана, так как m=b-ε, а в качестве М можно взять число M = b + ε, тогда для всех значений x, принадлежащих множеству .

Если точка а принадлежит области определения функции, то выберем в качестве m=min{b-ε, f(a)}. M = max{b+ε, f(a)}. Заметим, что в этом случае будут выполняться неравенства

1⁰. Если f(x) непрерывна в точке а, то она ограничена на множестве значений аргумента x, принадлежащих некоторой -окрестности точки а.

Справедливость следствия вытекает из того, что функция непрерывна в точке а, имеет в этой точке предел.

Теорема: Если функция f(x) непрерывна в точке а и значение этой функции в этой точке положительное(отрицательное), то значения функции f(x) будут положительными(отрицательными) на некотором множестве

Доказательство: Так как f(x) непрерывна в точке а, то для любого положительного числа ε найдётся соответствующее число(положительное) , такое, что для всех значений выполняется неравенство .

Последнее неравенство означает, что на множестве значений функции лежат .

Возьмём в качестве ε положительное число , тогда если f(a)>0, то

. Значения функции f(x) на множестве будут положительными ,если f(a)<0, то

.

Таким образом заключаем, что если значения функции в точке а, то а множестве функция f(x) также будет отрицательной.

К числу локальных свойств непрерывных функций относится рассмотренная ранее теорема о непрерывности суммы, разности, произведения, частного непрерывной функции, теорема о непрерывности сложной функции, теорема о непрерывности обратной функции.