25 Вопрос

Функция

Определение: Если каждому значению переменной Х ,принадлежат некоторые области,соответствует одно определённое значение другой переменной Y есть функция от Х,или записи y=f(x),y= (x). ( -независимая переменная)

Определение: Совокупность значений Х,для которого определяются значения функции Y,называются областью определения функции.

Способы образования функций.

1)Табличный (выписываются значения аргумента 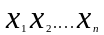,и соответствыющие значения ).

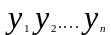2)Графический.

26 Вопрос

Предел функции.

Определение предел функции по Гейне: число b, называется пределом функции 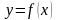, в точке a, если для любой последовательности значений аргумента сходящихся к точке a, и состоящих из элементов отличных от числа a. Соответствующая последовательность значений функций 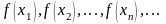сходится к числу b.

Если 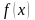имеет предел в точке a=b, то это записывают в виде:

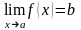
Определение предела функции по Коши: число b, называется пределом функции , в точке a, если для любого положительного числа , найдётся отвечающее ему положительное число , такое, что для всех значений 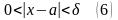, следовательно

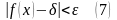
Теорема: Определение предела функции по Гейне и Коши равносильны.

При исследовании функций приходится видеть пределы, когда значение аргумента стремится к точке а, принимая значения >a (< a). В этом случае говорят о правых и левых пределах функции f(x) в точке а.

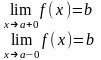
Определение: Число b называется пределом функции f(x) при x ∞ обозначается 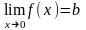, если для любой бесконечно большой последовательности значения аргумента {x_n}, соответствует последовательность значений функций {f(x_n)}.

Из приведённой теоремы вытекает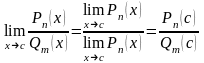

Таким образом замечаем, что предел рациональной дроби равен значению дроби в предельной точке ,при этом необходимо потребовать, чтобы .

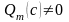Функция, обладающая таким свойством, называется непрерывной.

Теорема: Пусть две функции f(x) и g(x) заданы на одном и том же множестве {x} и имеют в точке а предел, соответственно равный b и c, тогда функции f(x)+g(x), f(x)-g(x), f(x)*g(x), f(x)/g(x) имеют в точке а пределы, соответственно равные b+c, b-c, b*c, b/c(в последнем случае c не равно 0).

27 Вопрос

Непрерывные функции.

Определение: Функция f(x) называется непрерывной в точке a, если она определена в этой точке и если предел функции в этой точке равен значению функции в точке a.

Определение: Функция f(x) непрерывна в точке a, если для любого положительного числа ε найдётся отвечающее ему положительное число b, такое, что для любого

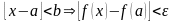
Определение: Функция f(x) называется непрерывной на множестве, если она непрерывна в каждой точке этого множества.

Определение: Точки ,в которых не выполняются условия непрерывности ,называются точками разрыва.

Классификация точек разрыва функции

Точка устранимого разрыва.

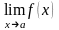Определение: Точка а называется точкой устранимого разрыва функции , если существует предел функции в точке а , то сама функция либо не определена в этой точке, либо ее значения отличаются от предельного значения функции в точке а.

Разрыв первого рода (конечный скачок)

Опр. Точка а называется точкой первого рода, если в этой точке существуют конечные левые и правые пределы, отличные друг от друга.

Разрыв второго рода.

Определение: Точка а называется точкой разрыва второго рода для функции 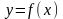, если в этой точке функция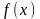 не имеет хотя бы одного из односторонних пределов, либо хотя бы из односторонних пределов бесконечен.

Определение: Функция называется кусочно-непрерывной на отрезке [ ] , если она определена во всех точках этого отрезка на сегменте [a,b] и непрерывна за исключением конечного их числа, в которых функция может терпеть разрывы 1-ого рода (конечные скачки), и кроме того функция должна обладать правым конечным пределом в точке 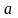, и левым конечным пределом в точке .

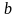Функция называется кусочно-непрерывной на интервале, если она является кусочно-непрерывной на любом отрезке в рассматриваемом интервале.