24 Вопрос

Монотонные последовательности.

Определение: Последовательность {X_n} называется монотонной, если она является либо не убывающей, либо невозрастающей.

Определение: Последовательность {X_n} называется неубывающей (невозрастающей), если все элементы этой последовательности, начиная со второго удовлетворяют неравенству .

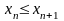
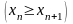Неубывающая и невозрастающая последовательность называются монотонной последовательностью.

Теорема(теорема о сходимости некоторой ограниченной последовательности): Если неубывающая (невозрастающая) последовательность ограничена сверху (снизу), эта последовательность является сходящейся.

Доказательство: Система отрезков {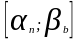 } наз. стягивающейся системой отрезков, если недостающий отрезок в предыдущем и если длина отрезка  0 при n 

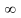
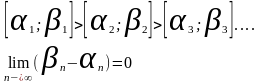
Следствии: У всякой стягивающейся системы отрезков существует единственная точка, принадлежащая всем отрезкам.

Число Е

Рассмотрим последовательность рациональных чисел n-ый член которой определяется

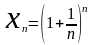
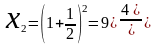(2)

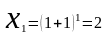
Покажем что последовательность n-ый член которой определяется соотношением (2), является сходящейся. Для этого покажем, что эта последовательность является возрастающей и ограниченной сверху.

Используя формулу Бинома – Ньютона соотношение 2 можно представить виде:

=

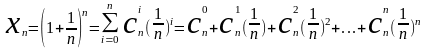Используя выражение для числа сочетаний 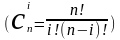, получим:

=

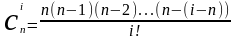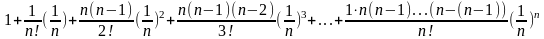
Перепишем последнее соотношение в виде

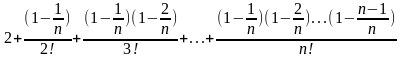= (3)

Используя представление (3), выпишем выражение для (n+1) элементов последовательности (4):

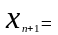
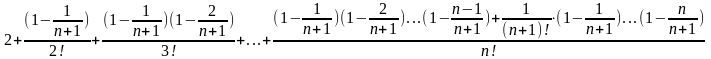
В выражении (3) присутствуют n слагаемых, в выражении (4) – (n+1) слагаемых.

Заметим, что последнее слагаемое в выражении (4) положительное.

Сравним между собой к-ое слагаемое соотношений (3),(4), где к меняется от 2 до n

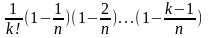
k-ое слагаемое в соотношении (4) будет иметь вид:

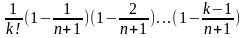
Сравнивая к-ые слагаемые, замечаем, что к-ое слагаемое выражения (3) < k-ого слагаемого выражения (4). Откуда вытекает выполнение неравенства: 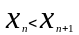, т.е. рассматриваемая последовательность является возрастающей.

Покажем, что эта последовательность является ограниченной. Заменим в выражении (3) каждую круглую скобку 1. В результате получим неравенство: 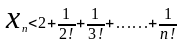Используя очевидное соотношение

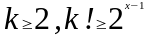
Используя очевидное неравенство для и оценки (5) получим что

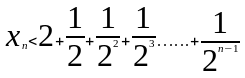Используя формулу бесконечно убывающей геометрической прогрессии парвую часть представем в виде

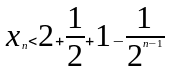
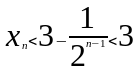
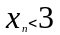
Рассматривая последовательность возрастающую и которая ограниченна сверху следовательно она имеет придел. Следуя Леонарду Геллеру этот предел обозначается в виде

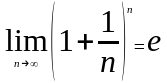
Вещественное число

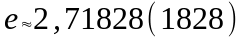
Если последовательность является бесконечно большой то её предел равен бесконечности

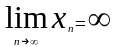
Если не является сходящейся то её называют расходящейся.