22 Вопрос

Последовательности.

Определение: Если каждому значению n из натурального ряда {1,2,3,…,n} ставится в соответствие некоторое вещественное число, то множество занумерованных вещественных чисел 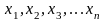называется числовой последовательностью

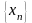
Отдельные числа Хn называются элементами или членами последовательности,

Последовательность может быть задана различными способами:

1)Словесным описанием: числа 0,3; 0,33; 0,333, являются последовательностью рациональных чисел приближающих число 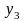по недостатку с точностью до 0,1: 0,01: 0,001, …

2)Последовательность может быть задана заданием формулой, для вычисления n-го члена последовательности.

Пример:

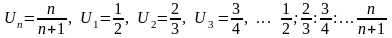
3) Последовательность может быть задана с помощью рекуррентной формулы. При этом задаются несколько членов последовательности и формула, позволяющая вычислить следующие члены последовательности исходя из заданных:

Определение: Последовательность называется ограниченной сверху(снизу), если существует такое вещественное число M(m), такое что все элементы последовательности удовлетворяют неравенству 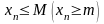. При этом M(m) называется верхней(нижней) гранью последовательности.

Пример:

1)

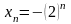
-2; -4: -8; -16

Эта последовательность ограничена сверху.

2)

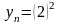
2, 4, 8, 16

Эта последовательность ограничена сверху.

Определение: Последовательность называется ограниченной с обоих сторон или просто ограниченной, если она ограничена и сверху и снизу.

Пример:

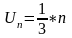
1/3; 1/9; 1/27

И мы видим, что всякая последовательность, ограниченная только сверху или снизу, не является ограниченной.

Определение: Последовательность является ограниченной, если для любого положительного числа А найдётся элемент последовательности, удовлетворяющий неравенству

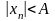
Определение: Последовательность является неограниченной, если для любого положительного числа А найдётся элемент последовательности, удовлетворяющий неравенству

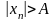
Пример: 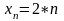неограниченная последовательность

> > >

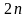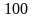
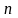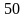
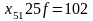О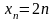 пределение: Последовательность называется бесконечно большой, если для любого положительного вещественного числа А найдется номер N, такой что для любого 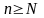будет выполняться неравенство 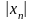>А.

.Пример: 1,2,1,4,1,6 1,2n

Определение: Последовательность называется бесконечно малой последовательностью, если для любого положительного числа ε найдется номер N, такой что для всех будет выполняться неравенство < ε.

Основные свойства бесконечно малых последовательностей.

Теорема1: Есл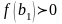и и 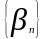- две бесконечно малые последовательности, то последовательность 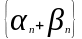также является бесконечно малой последовательностью.

Доказательство: Фиксируем некоторое положительное число > 0, т.к 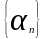является бесконечно малой, то для заданной величины найдется номер N, такой что при всех n N, будет выполняться неравенство:

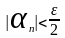
Аналогично для бесконечно малой последовательности 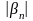найдется номер, 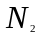такой что при всех n будет выполняться неравенство

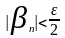
Обозначим в качестве N = max {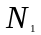 }, тогда для всех n N будут одновременно выполняться оба записанные неравенства. Используя 2 свойство абсолютной величины, + < + <

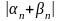
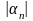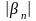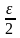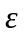
Теорема 2: Разность двух бесконечно малых последовательностей является бесконечно малой последовательностью.

Доказательство теоремы аналогично доказательству теоремы 1. Используя 3 свойство абсолютной величины: -

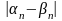Следствие Т1, Т2.

Алгебраическая сумма конечного числа бесконечно малых последовательностей дает бесконечно малую последовательность.

Теорема 3: Произведение ограниченной последовательности 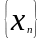на бесконечно малую последовательность дает бесконечно малую последовательность.

Доказательство: Последовательность является ограниченной => существует такое вещественное положительное число А, что все элементы

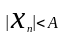
Фиксируем положительное число > 0. Т.к последовательность является бесконечно малой, то для фиксированного числа найдется номер N , такой что при всех n N будет выполняться неравенство

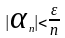
Таким образом получаем

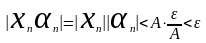
Откуда следует справедливость теоремы.

Теорема 4:Всякая бесконечно малая последовательность является ограниченной.

Доказательство: Рассмотрим последовательность

Если эта последовательность бесконечно малая, то для зафиксированного числа найдется номер N , такой что при всех n N будет выполняться неравенство

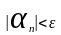
Другими словами все элементы бесконечно малой последовательности начиная с номера N лежат в -окрестности нуля. Вне этой -окрестности находится конечное число элементов.

Обозначим через А = max

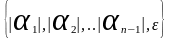
Тогда для всех элементов будет справедливо неравенство

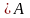
Следствие Т4

Произведение конечного числа всех бесконечно малых последовательностей является бесконечно малой последовательностью.

Теорема5:Если все элементы бесконечно малой последовательности равны одному и тому же числу c, с = 0.

Т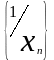 еорема6: Если последовательность бесконечно большая последовательность, то начиная с некоторого числа n определено частное двух последовательностей 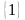и , которое представляет собой бесконечно малую последовательность.

Если все элементы бесконечно малой последовательности отличны от нуля, то частное последовательности 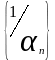представляет собой бесконечно большую последовательность.