17 Вопрос

Поверхность второго порядка

Определение: Геометрическое место точек, координаты которых удовлетворяют уравнению

называют поверхностью второго порядка.

Первые шесть слагаемых называют квадратичной формой от трёх переменных x,

y, z.

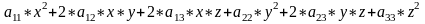Квадратичная форма (5) может быть представлена в матричном виде:

Следующие три слагаемых уравнения (4) называются линейной формой от трёх переменных:

В матричном виде уравнение (6) можно представить как

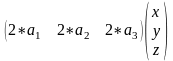
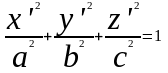Построив новый ортогональный базис из собственных векторов матрицы (5’), приведём квадратичную форму к каноническому виду соответствующей матрицы диагональной формы.

Таким образом поверхность второго порядка можно записать в виде:

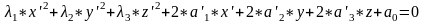Величины 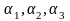называются собственными значениями матрицы квадратичной формы. Если собственные значения не равны 0 (≠0), то за счет переноса начала координат уравнение (4’) существенно упрощается:

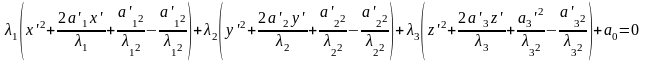
В этом случае уравнение поверхности второго порядка примет вид:

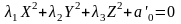
Рассмотрим некоторые канонические формы поверхностей второго порядка.

Поверхности вращения

Определение: Поверхность S называется поверхностью вращения, если ось образована из окружностей, центры которой лежат на прямой, а сами окружности расположены в осях перпендикулярно.

Рассмотрим плоскость P , проходящую через прямую d и линию l, лежащую в плоскости Р. Поверхность вращения можно рассматривать от вращения l вокруг d.

Выберем на прямой d начало координат О вектор 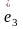направим по прямой d,

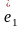расположим в плоскости Р.

Таким образом на плоскости Р мы вывели декартовую систему координат 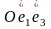и линию l можно задать в виде

Возьмем на плоскости вращения точку М (x,y,z) расположенную на окружности радиусом

Точка М лежит на плоскости вращения тогда и только тогда, когда на l существует точка М₁, получаемая из М движением по окружности радиусом r М₁(x,y,z). Точка М₁ лежит в плоскости Р и следовательно y₁=0 z₁=z точки М. координата x₁ по абсолютной величине совпадает с радиусом окружности. М лежит на поверхности вращения, если ее координаты удовлетворяют уравнению

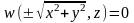(1) уравнение поверхности вращения может быть также представлено в виде

(1’)

18 Вопрос

Эллипсоид

Рассмотрим поверхности вращения, получаемые от вращения эллипса вокруг оси симметрии.

Рассмотрим уравнение эллипса в виде:

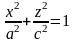, где а>с

С учетом формул (1) поверхность вращения эллипса вокруг малой оси будет иметь вид: (2)

Вращая эллипс вокруг большей оси, т.е рассматривая уравнение

получим поверхность вращения в виде

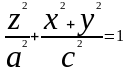
(2’’)

Первая поверхность называется сжатым эллипсоидом вращения:

Вторая поверхность дает нам вытянутый эллипсоид вращения:

П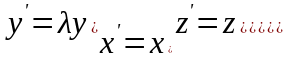 реобразуем поверхность 2, сжав каждую точку эллипсоида вращения к поверхности y=0,т.е. совершим преобразование

тогда получим поверхность, уравнение которой будет иметь вид

(3), где

Поверхность определяемая уравнением (3) называется эллипсоидом

Частным случаем эллипсоида, при a=b=c является поверхность сферы, уравнение которой имеет вид

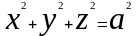
Конус второго порядка

Рассмотрим на плоскости P пару пересекающихся прямых задаваемых в системе координат , уравнение . (4)

Вращая пару пересекающихся прямых (4) вокруг оси z(аппликат), получим поверхность вращения , уравнение которое имеет вид:

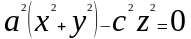(5)

Поверхность (5) носит название прямого кругового конуса

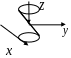
Сжав точки поверхности конуса в плоскости y=0 , преобразование

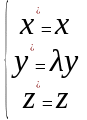
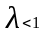
Получим поверхность вида (6)

Поверхность заданная уравнением (6) называется конусом второго порядка или просто конусом .

Поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение (6), называется конусом или конусом второго порядка. Конус состоит из прямы линий, проходящих через начало координат. Сечение конуса плоскостью с уравнением 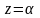при резке представляет собой эллипс.