1 Вопрос

Метод Гаусса . Решение систем линейных уравнений.

Рассмотрим систему линейных уравнений :

О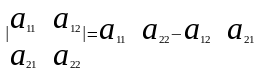 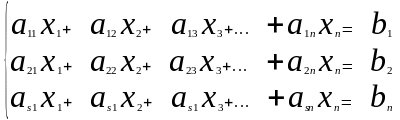тметим что в системе (1) присутствует S – уравнений и n неизвестных. Натуральные числа S,n ни не связаны друг с другом.

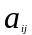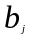, - некоторые числа в дальнейшем, если не оговорено противное, будем предполагать эти числа вещественными.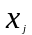 – неизвестная переменная. Совокупность неизвестных элементов ( , 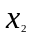… 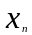) можно рассматривать как упорядоченный n мерный вектор ( , … ).

При исследовании системы (1) рассматривают прямоугольную таблицу коэффициентов, называемую матрицей (А).

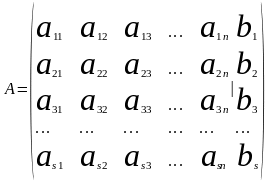
Принято говорить ,что матрица (2) имеет размеры S*n . Добавление к матрице А столбца свободных членов приводит к новой матрице , которую принято называть расширенной матрицей.

Часто, чтобы показать особенность последнего столбца его отделяют вспомогательной черточкой.

Определение: Упорядоченную совокупность чисел (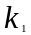 , 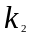… 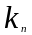)= 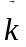(n мерный вектор ) называется решением системы (1) ,если подстановка вместо вектора 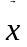вектор обращает каждое уравнение системы (1) в тождество.

Определение: Система уравнений называется совместной, если она обладает решением, и несовместной, если она не обладает решением. Совместная система называется определенной, если решение единственно и неопределенной, если решений бесконечное множество.

О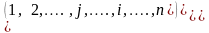 пределение: Две системы линейных уравнений называются эквивалентными (равносильными), если они обе несовместны или обе совместны и обладают одинаковыми наборами решений.

Определение: преобразование системы (1) вида:

а)перемена местами уравнения системы.

б)умножение уравнения системы на число отличное от нуля.

в)прибавление к одному уравнению системы другого уравнения, умноженного на некоторое число отличного от нуля - называются элементарными.

2 Вопрос

Элементы комбинаторики

Определение: Размещением из n элементов по p в каждом называются такие комбинации, состоящие из p элементов, которые отличаются друг от друга либо самими элементами, либо порядком их расположения.

П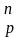 ринято различать размещение с повторениями и размещением без повторений. Очевидно, что размещения с повторениями совпадают с упорядоченным набором р-элементов, выбираемых из множества n-элементов. (а₁,а₂, а₃, … , а_n). n^p – число размещений с повторениями; число размещений без повторений A и равно произведению 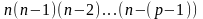. Поскольку в этом случае первый элемент а₁ выбирается из множества n-элементов, второй а₂ выбирается из 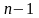элементов, последний из 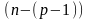элементов. Частным случаем размещения является перестановка.

Определение: Любое расположение первых n-натуральных чисел называется перестановкой.

Ч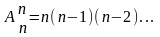 исло перестановок обозначается P_n= 3*2*1*=n! (!– факториал)

0!=0

1!=1

2!=1*2=2

3!=1*2*3=6

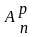4!=1*2*3*4=24

С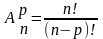 учетом понятия факториала можно представить в виде

Определение: Сочетаниями из n-элементов по р в каждом называют такие комбинации р-элементов, которые выбираются из множества n-элементов без повторений, причем порядок расположения элементов не имеет значения.

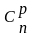
- число сочетаний.

Рассмотрим комбинацию из (a,b,c) элементов. Выпишем всевозможные комбинации этих элементов с учетом порядка (a,b,c) (b,a,c) (c,a,b) (a,c,b) (b,c,a) (c,b,a). Таким образом получили 6 комбинаций, называемых размещениями без повторений.

С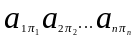 точки зрения сочетания в этом случае речь идет об одной комбинации. Упорядочив каждое сочетание, получим все множество размещений. Каждое сочетание, состоящее из p-элементов можно упорядочить, превратив в p! Размещений. Таким образом, 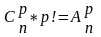отсюда вытекает, что число сочетаний