1.14. Применение линий без потерь.
Линии без потерь
длиной в четверть волны применяются в
качестве согласующего элемента между
какой либо линией без потерь и приемником
с резистивным сопротивлением на ее
конце
,
не равным волновому сопротивлению
линии. Например, при помощи линии
четвертьволновой линии можно согласовать
линию (без потерь), питающую антенну, с
самой антенной, входное сопротивление
которой чисто активное.
Найдем входное
сопротивление четвертьволновой линии
(
),
нагруженной на антенну сопротивлением
.
На основании выражения (1.29)
.
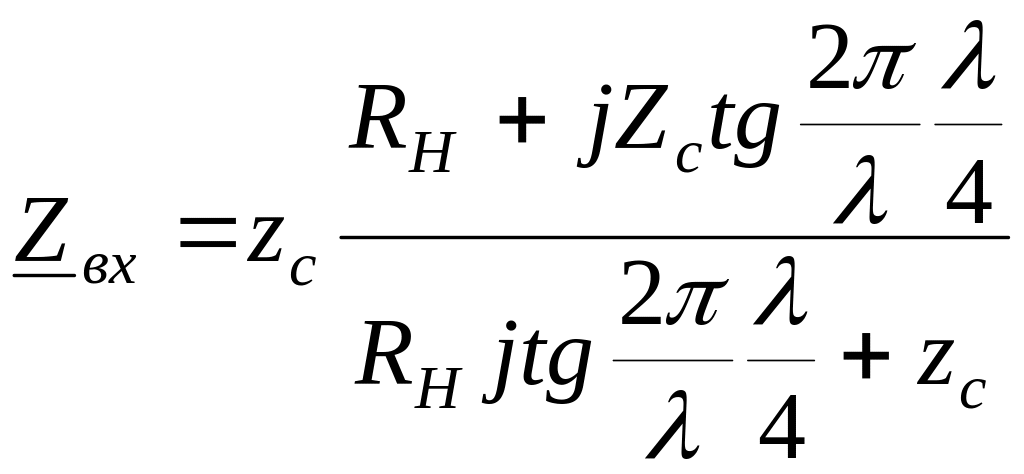Т.к.
,
то
.
Для согласования
питающей линии с антенной необходимо,
чтобы
,
где
- волновое сопротивление питающей линии.
Отсюда требуемое значение волнового сопротивления
.
В этом случае четвертьволновая линия без потерь называется четвертьволновым трансформатором, т.к. она трансформирует волновое сопротивление питающей линии, согласовывая его с сопротивлением нагрузки.
2. Электростатическое поле
2.1. Общие сведения об электромагнитном поле.
Третья часть курса ТОЭ посвящена изучению теории электромагнитного поля, в которой рассмотрены физические явления и процессы, происходящие в электромагнитном поле, и методы их расчета. Эти явления и процессы лежат в основе действия большого числа различных электромагнитных и электронных приборов и устройств, широко применяемых на практике, а методы расчета физических явлений и процессов, рассмотренные в курсе Электромагнитного поля, используют при расчете и конструировании этих приборов и устройств.
Под электромагнитным полем понимают вид материи, характеризующийся совокупностью взаимно связанных и взаимно обусловливающих электрического и магнитного полей. Электромагнитное поле обладает характерными для него электрическими и магнитными свойствами, доступными наблюдению. Силовое воздействие поля на электрические заряды и токи положено в основу определения основных векторных величин, которыми характеризуют поле: напряженности электрического поля и индукции магнитного поля .
Значения и как взаимно связанных характеристик единого электромагнитного поля зависят от условий наблюдения этого поля. Они оказываются различными в неподвижной и в подвижной системах координат. Так, электрический заряд, движущийся в некоторой системе координат прямолинейно с постоянной скоростью, создает вокруг себя в этой системе и электрическое, и магнитное поле. Но наблюдатель, движущийся с той же скоростью и в том же направлении, обнаружил бы только электрическое поле, так как по отношению к нему заряд неподвижен.
Электромагнитное поле может самостоятельно существовать в виде электромагнитных волн в вакууме. Это свидетельствует о том, что поле, являясь формой материи, может существовать при отсутствии другой формы материи — вещества. Наряду с этим, электромагнитное поле обладает такими характеристиками, которые присущи веществу, а именно: энергией, массой и количеством движения.
Масса электромагнитного поля в единице объема определяется как частное от деления энергии поля в единице объема на квадрат скорости распространения электромагнитной волы в вакууме, равной скорости света. Количество движения электромагнитного поля, отнесенное к единице объема, равно произведению массы поля в единице объема на скорость распространения электромагнитной волны в вакууме.
При распространении электромагнитного поля одновременно с движением потока электромагнитной энергии происходит перемещение массы поля и количества движения.
Масса электромагнитного поля, заключенная в единице объема, несоизмеримо мала по сравнению с массой (плотностью) всех известных веществ. Даже при максимально достижимых в настоящее время значениях напряженностей электрического и магнитного полей масса поля в единице объема оказывается равной 10-16 … 10-18 кг/м3. Тем не менее, наличие массы поля имеет принципиальное значение, поскольку в этом отражена известная инерционность процессов в электромагнитном поле. В одних случаях электромагнитное поле распределено в пространстве непрерывно, в других обнаруживает дискретную структуру, проявляющуюся в виде квантов излученного поля. Электромагнитное поле может превращаться в вещество, а вещество — в поле. Так, электрон и позитрон превращаются в два кванта электромагнитного излучения, а при исчезновении фотона возникает пара: электрон и позитрон. Превращение поля в вещество, а вещества в поле соответствуют превращению одного вида материи в другой. Пространство и время являются формами существования электромагнитного поля.