1.10. Холостой ход и короткое замыкание линии с потерями.

Рассмотрим холостой ход линии ( ). Изменив напряжение в начале линии так, чтобы напряжение в конце линии осталось равным , из уравнений (1.21) получим:

(1.26)

Если в короткозамкнутой линии ( ) изменить напряжение в начале линии так, чтобы ток в конце линии стал равным , получим:

(1.27)

Из (1.21), (1.26) и (1.27) можно получить:

.

Этими формулами удобно пользоваться в расчетах.

1.11. Линии без потерь.

Если принять равными нулю сопротивление проводов линии ( ) и проводимость утечки между проводами ( ), то получим так называемую линию без потерь – идеализацию реальной длинной линии.

В радиотехнике очень часто рассматривают двухпроводные воздушные линии и коаксиальные кабели как линии без потерь.

Для такой линии получаем:

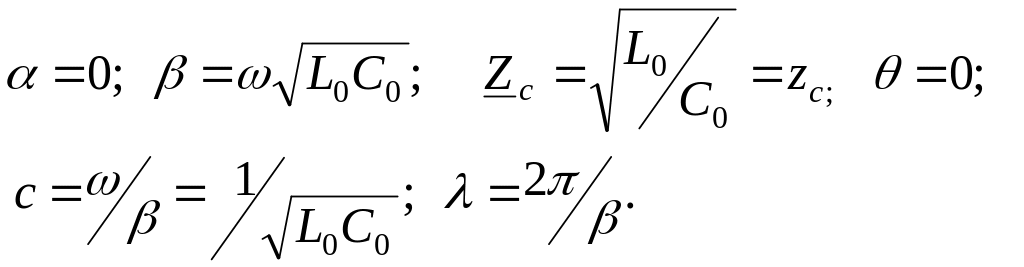
В линии без потерь нет ослабления волн, а волновое сопротивление чисто активное и не зависит от частоты.

Фазовую скорость можно записать в виде

,

где - абсолютные диэлектрическая и магнитная проницаемость среды.

Учитывая, что скорость света в вакууме , фазовая скорость .

Для воздушных линий и фазовая скорость в вакууме совпадает со скоростью света. Для кабельных линий и . В линиях без потерь , т.е. токи прямой и обратных волн совпадают по фазе с напряжениями.

Уравнения длинной линии с гиперболическими функциями от комплексного аргумента переходят в уравнения с круговыми функциями от действительного аргумента, т.е:

,

. (1.28)

Входное сопротивление линии без потерь

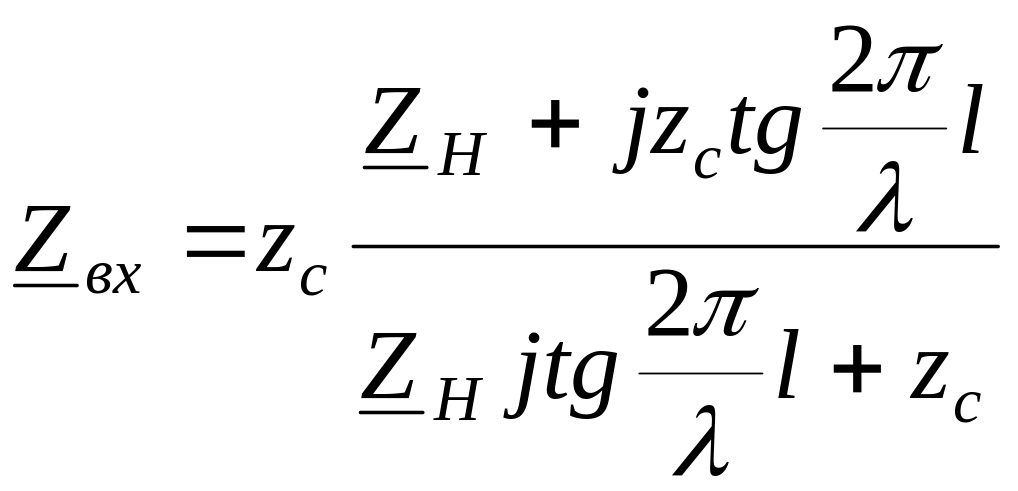. (1.29)

Мгновенные значения при и :

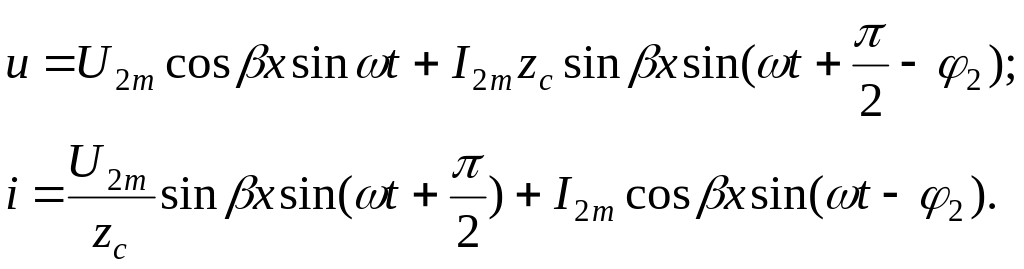
Рассмотрим свойства линии без потерь длиной в четверть и в половину длины волны.

При , тогда из (1.28) следует

,

т.е. напряжение (ток) в начале линии пропорционален току (напряжению) в конце линии и опережает их по фазе на угол 90⁰.

При и ,

т.е. напряжение и ток в начале линии равны по абсолютному значению и противоположны по фазе напряжению и току в конце линии.

1.12. Стоячие волны.

Рассмотрим режимы, при которых активная мощность в конце линии без потерь равна нулю. Это может быть при холостом ходе, коротком замыкании и чисто реактивной нагрузке.

При холостом ходе из (1.28) следует

. (1.30)

При мгновенные значения напряжения и тока имеют вид:

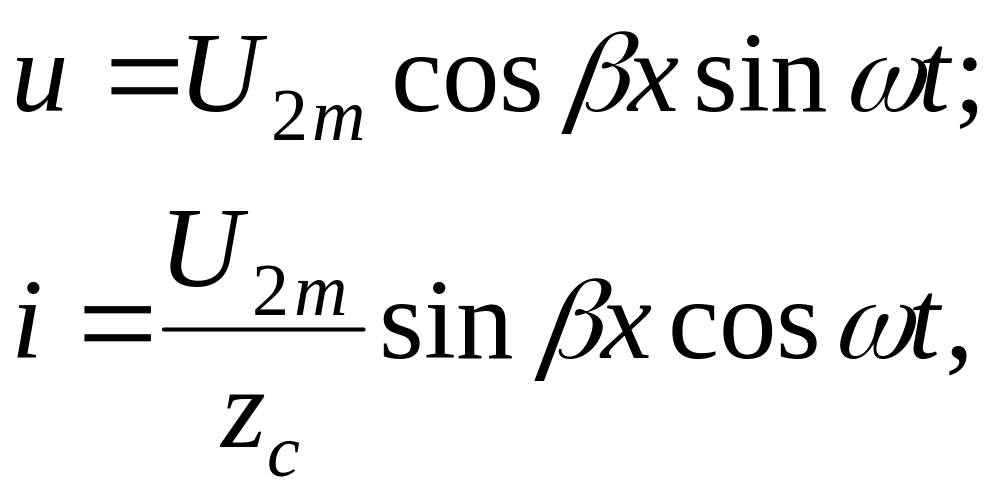(1.31)

и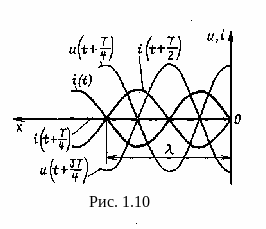 представляют собой уравнения стоячих волн.

Стоячей волной называется процесс, получающийся от наложения прямой и обратной волн с одинаковыми амплитудами.

При холостом ходе на конце линии (х = 0) и в точках, отстоящих от конца на расстояниях , где k - целое число, имеем в любой момент времени максимумы напряжения, называемые пучностями, и нули тока, называемые узлами (рис. 1.10). На расстояниях от конца линии наблюдаются узлы напряжения и пучности тока. Узлы и пучности тока и напряжения неподвижны. Узлы тока совпадают с пучностями напряжения и наоборот.

При возникновении стоячих волн электромагнитная энергия от начала к концу линии не передается. Однако на каждом отрезке линии, равном четверти длины волны, запасена некоторая электромагнитная энергия. Эта энергия периодически переходит из энергии электрического поля в энергию магнитного поля и наоборот. В моменты времени, когда ток вдоль всей линии оказывается равным нулю, энергия переходит в энергию электрического поля. В моменты времени, когда напряжение вдоль всей линии равно нулю, а ток достигает максимального значения, вся энергия переходит в энергию магнитного поля.

Картина стоячей волны напряжения (тока) при коротком замыкании на конце линии качественно повторяет картину стоячей волны тока (напряжения) при холостом ходе линии.