1.2. Уравнения однородной двухпроводной линии.

Составим дифференциальные уравнения, которым удовлетворяют напряжения и токи в любом сечении двухпроводной линии (линия связи – двухпроводный кабель со скрученными проводами).

Условимся называть верхний провод двухпроводной линии прямым, а нижний провод – обратным. Выберем положительные направления тока и напряжения.

Первичными параметрами однородной линии являются:

R₀ – активное сопротивление единицы длины прямого и обратного проводов;

L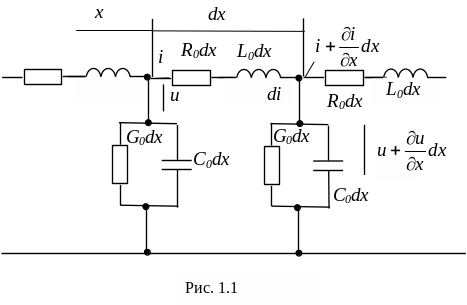 ₀ – индуктивность единицы длины петли, образуемой прямым и обратным проводом;

G₀ – проводимость (утечка) на единицу длины между проводами;

С₀ – емкость на единицу длины между проводами.

Разобьем линию (рис. 1.1) на участки длиной dx, где х – расстояние, отсчитываемое от начала линии. На длине dx активное сопротивление равно R₀dx, индуктивность - L₀dx, проводимость утечки - G₀dx и емкость - С₀dx. Обозначим ток в начале рассматриваемого участка линии через i и напряжение между проводами в начале участка через u. Сопротивление R₀dx и индуктивность L₀dx будем считать включенными в один провод. Ток и напряжение являются в общем случае функциями расстояния вдоль линии х и времени t. Поэтому в уравнениях использованы частные производные от u и от i по времени t и по расстоянию s.

О

1

2

бозначим для некоторого момента t ток в начале участка i, а в конце участка ток для того же момента времени обозначим ,

где - скорость изменения тока в направлении х;

– приращение тока на пути dx.

Аналогично, обозначим напряжение в начале участка и, а в конце участка для того же момента времени - .

Составим:

- уравнение по второму закону Кирхгофа для замкнутого контура, образованного участком линии длиной dx, обойдя его по часовой стрелке;

- уравнение по первому закону Кирхгофа для узла 2 с учетом напряжения в конце участка:

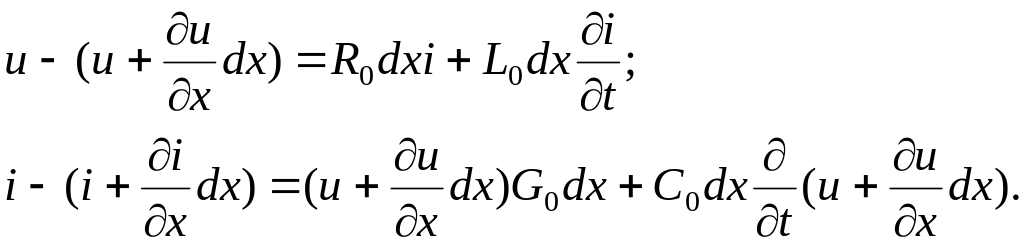(1.1)

Приводя подобные члены, пренебрегая величинами второго порядка малости и сокращая на dx, получаем дифференциальные уравнения:

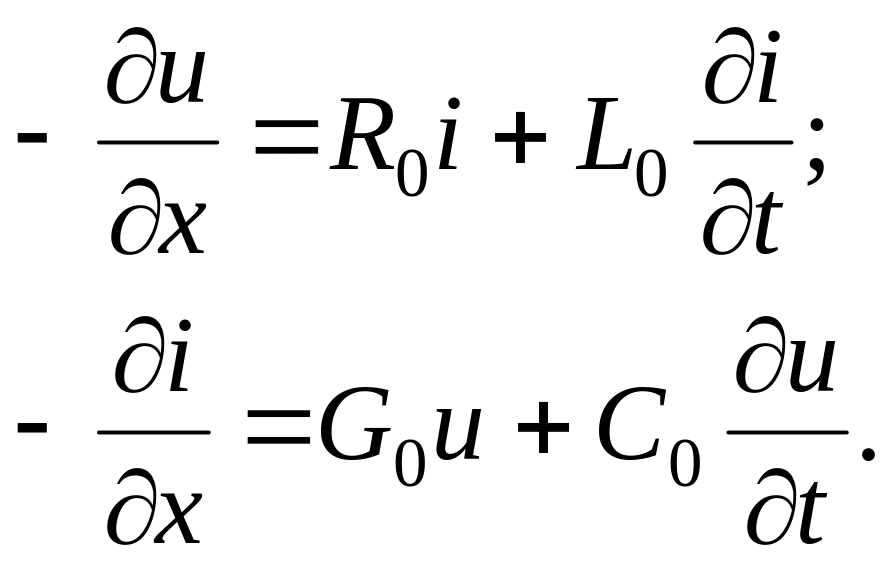(1.2)

Решение полученной системы уравнений в частных производных при определенных начальных и граничных условиях дает возможность определить ток и напряжение как функции расстояния от начала линии и времени. Эти уравнения справедливы при любых изменениях тока и напряжения во времени.

1.3. Установившийся режим в однородной линии.

Рассмотрим установившийся режим в однородной линии при синусоидальном источнике питания. Уравнения (1.2) для стационарного гармонического тока можно записать в комплексной форме:

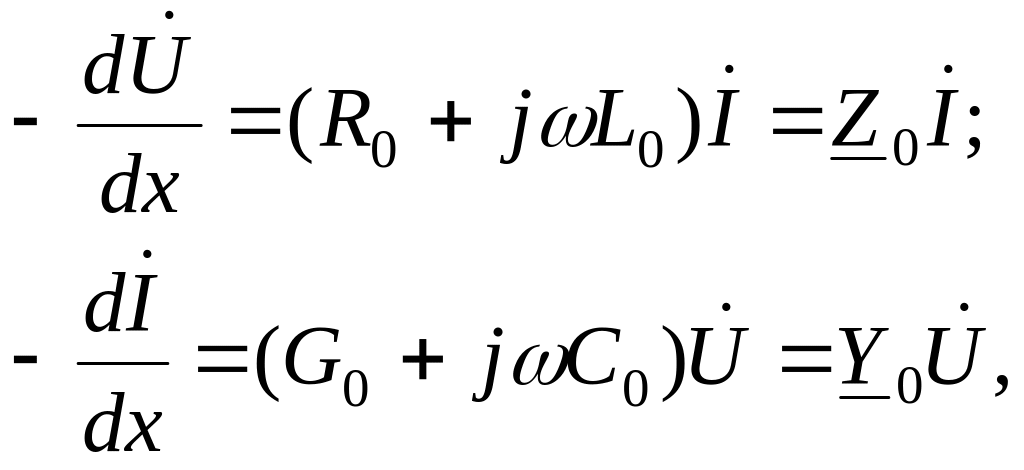(1.3)

где - комплексное сопротивление единицы длины линии;

- комплексная проводимость единицы длины линии.

Продифференцируем уравнения (1.3) по переменной х:

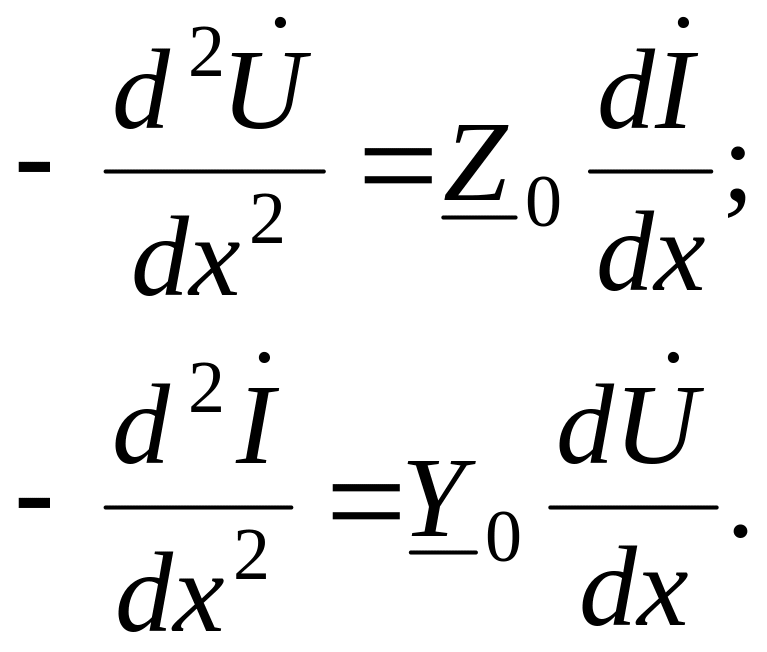
Вместо и в правой части подставим их значения из уравнений (1.3). Полу чим:

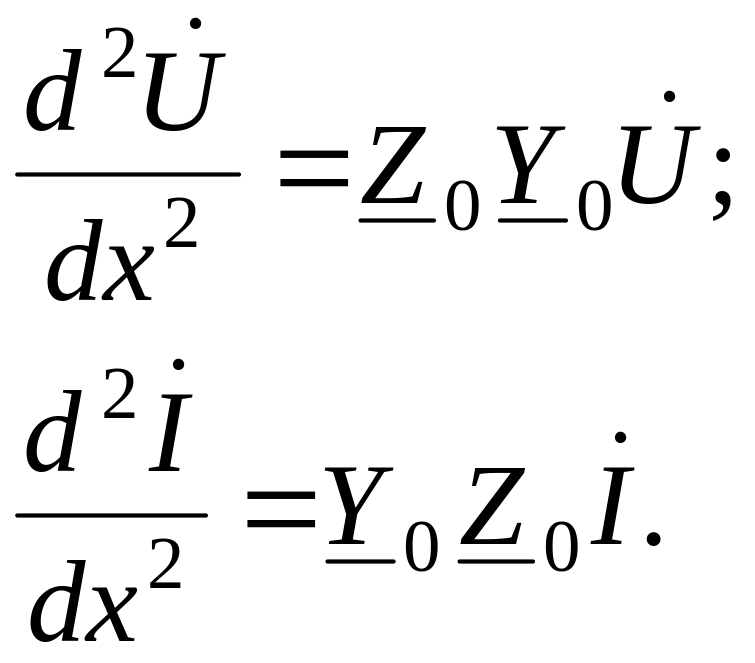(1.4)

Эти уравнения, определяющие изменения комплексных напряжений и токов вдоль линии, имеют одинаковый вид. Поэтому достаточно найти, например, закон изменения напряжения , а ток получить из уравнений (1.3).

Решение линейного дифференциального уравнения второго порядка для комплексного напряжения имеет вид

, (1.5)

где - комплексные постоянные интегрирования;

γ - комплексная величина, называемая коэффициент распространения линии

(1.6)

- коэффициент затухания;

- коэффициент фазы.

Ток согласно уравнению (1.3)

. (1.7)

Знаменатель, имеющий размерность сопротивления, называется волновым сопротивлением линии и обозначается . Рассматривая однородную линию как четырехполюсник, легко показать, что волновое сопротивление линии совпадает с характеристическим сопротивлением четырехполюсника. Поэтому в дальнейшем волновое сопротивление будем обозначать .

, (1.8)

где - аргумент волнового сопротивления. (1.9)

Волновое сопротивление и коэффициент распространения называются вторичными параметрами однородной линии.

Подставив в уравнение для тока (1.7), запишем

. (1.10)

Так как и , то мгновенные значений напряжения и тока:

; (1.11)

. (1.12)

Каждое из слагаемых правой части двух последних уравнений можно рассматривать как бегущую волну, движущуюся в направлении возрастания или убывания координаты х и затухающую в направлении движения.

Основными характеристиками бегущей волны являются фазовая скорость и длина волны.

Фазовой скоростью волны с называется скорость перемещения фазы колебания, которая в течении времени t и по мере увеличения расстояния х, пройденного волной, остается постоянной, т.е.

, откуда , и

, (1.13)

а для правого слагаемого уравнения (1.11) значение фазовой скорости такое же, но с обратным знаком. Следовательно, эти слагаемые могут рассматриваться как волны, движущиеся в противоположных направлениях.

Длиной волны называется расстояние между ближайшими двумя точками, взятое в направлении распространения волны, фазы колебания в которых различаются на . Следовательно, для первого слагаемого получим

,

откуда и

т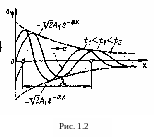 .е. за время, равное периоду волна пробегает расстояние, равное длине волны.

Условимся волну, движущуюся от начала линии называть прямой, а движущуюся от конца линии – обратной.

Затухающая прямая волна представлена на рис. 1.2.

Выберем положительные направления напряжений и токов отдельных волн от прямого провода к обратному.

Из (1.11) и (1.12) следует, что напряжение есть сумма напряжений прямой и обратной волн, а ток - разность токов прямой и обратной волн, тогда

где .

Токи и напряжения как прямой, так и обратной волны связаны между собой законом Ома:

(1.14)

С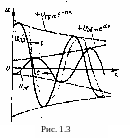 ледует иметь в виду, что физически существуют только результирующие ток и напряжение , а разложение их на прямые и обратные волны лишь удобный прием.

Кривые распределения мгновенных значений напряжений и токов также имеют волнообразный характер (рис. 1.3).

Получим выражения для напряжения и тока в любой точке линии через напряжение и ток в начале линии.

Перепишем уравнения (1.5) и (1.7):

;

, (1.15)

Предполагая, что в начале линии (х = 0) напряжение и ток , из уравнений (1.15) найдем постоянные интегрирования и .

; ;

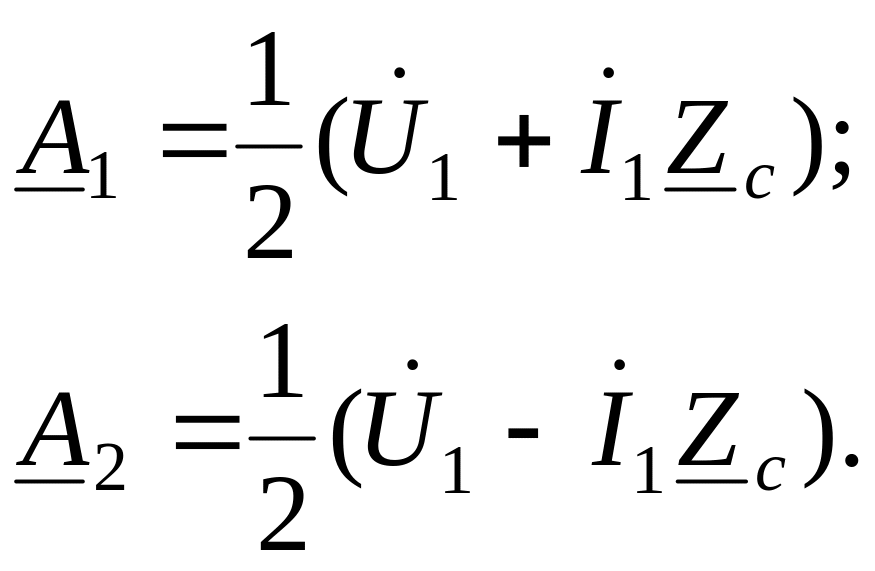(1.16)

С учетом (1.16) уравнения (1.5) и (1.7) для токов и напряжений в любой точке линии ( ) можно записать так:

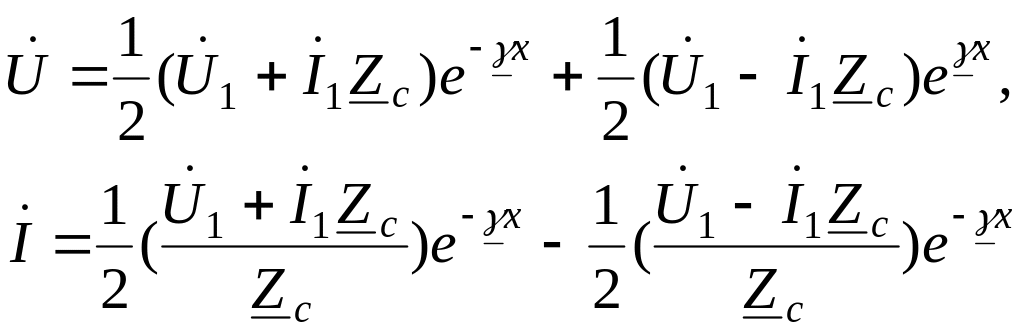. (1.17)

Подобным образом получим выражения для напряжения и тока в любой точке линии через напряжение и ток в конце линии:

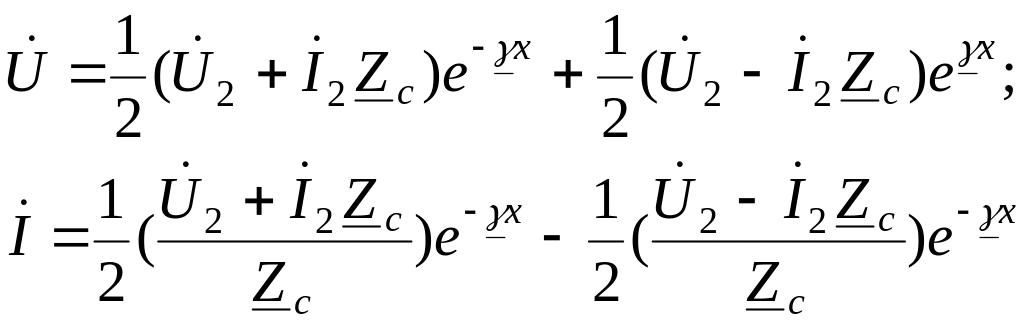. (1.18)