5.8. Электродинамические потенциалы.

Уравнения Даламбера.

Непосредственное решение уравнений Максвелла связано с большими математическими трудностями. Для упрощения решения этой задачи вводятся расчетные вспомогательные функции координат и времени - электродинамические векторный и скалярный потенциалы и .

Воспользовавшись уравнениями Максвелла и уравнениями , , получим основные соотношения для этих функций. Подставим во второе уравнение Максвелла

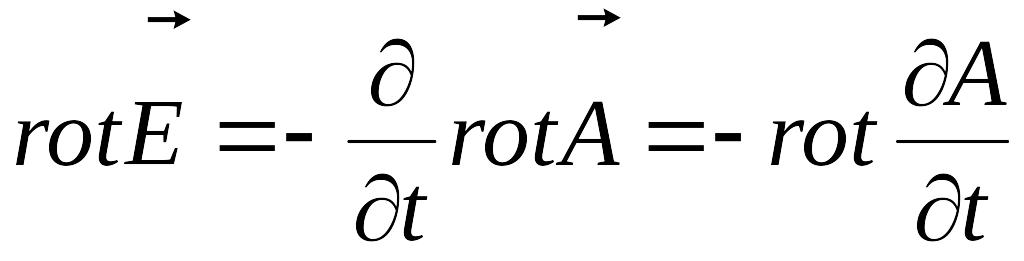или .

Полученное равенство говорит о том, что «вихрь» некоторого вектора всегда равен нулю. Это позволяет выразить вектор как градиент скалярной функции, удовлетворяющей как переменному, так и стационарному полю. Следовательно, или

, (5.15)

где φ – электродинамический скалярный потенциал.

Если поле стационарное, то , следовательно,

. (5.16)

Электродинамический потенциал , как и электродинамический потенциал , участвует в образовании магнитного поля.

Связь между и определяется соотношением

. (5.17)

Возьмем дивергенцию от равенства (5.15).

. Так как , получим

, или

. (5.18)

Это - уравнение для нахождения скалярного электродинамического потенциала .

Получим формулу, по которой определяют векторный электродинамический потенциал .

По первому уравнению Максвелла .

Так как , , , , имеем

,

.

Из векторного анализа известно, что

.

Поэтому .

Полученное выражение содержит две неизвестные величины - и . Исключим одну из них.

Электродинамический вектор-потенциал не определяется однозначно, он является расчетной функцией, которая выбирается из удобства расчета, но не должна противоречить физической стороне вопроса, т.е. должна отражать изменение поля.

В стационарном магнитном поле , а в переменном .

Подставив значение в формулу (5.17), получим

.

Отсюда определим уравнение для нахождения вектора-потенциала

. (5.19)

Уравнения (5.18) и (5.19) называются уравнениями Даламбера

- (5.20)

Если в рассматриваемом объеме нет токов проводимости и свободных зарядов, то получим частный случай уравнений Даламбера - волновые уравнения электромагнитного поля (5.21), которые характеризуют процесс распространения электромагнитного поля в областях, где нет источников этого поля:

. (5.21)

Для стационарного поля уравнения Даламбера переходят в уравнения Пуассона

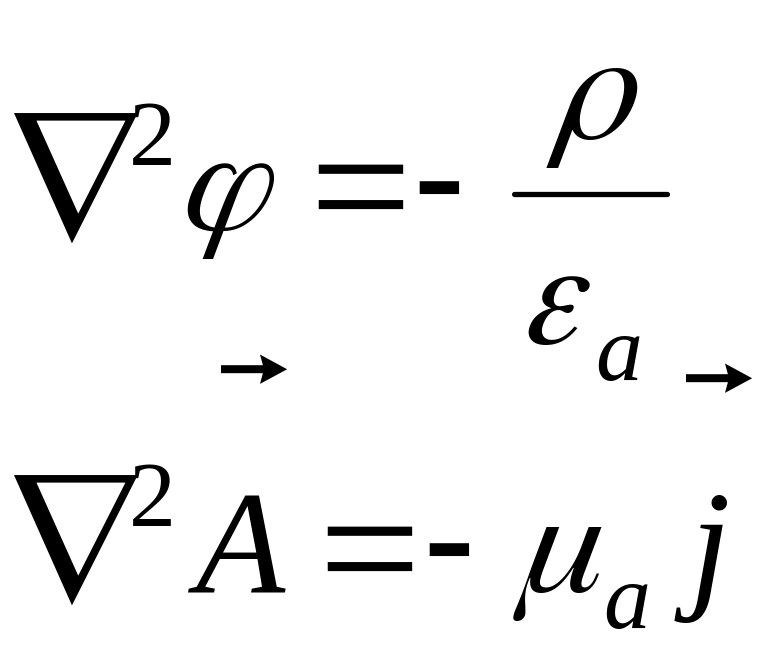. (5.22)

При отсутствии в рассматриваемом объеме токов проводимости и свободных зарядов эти уравнения переходят в уравнения Лапласа

. (5.23)

5.9. Запаздывающие потенциалы.

Решением уравнений Даламбера являются следующие равенства:

, ,

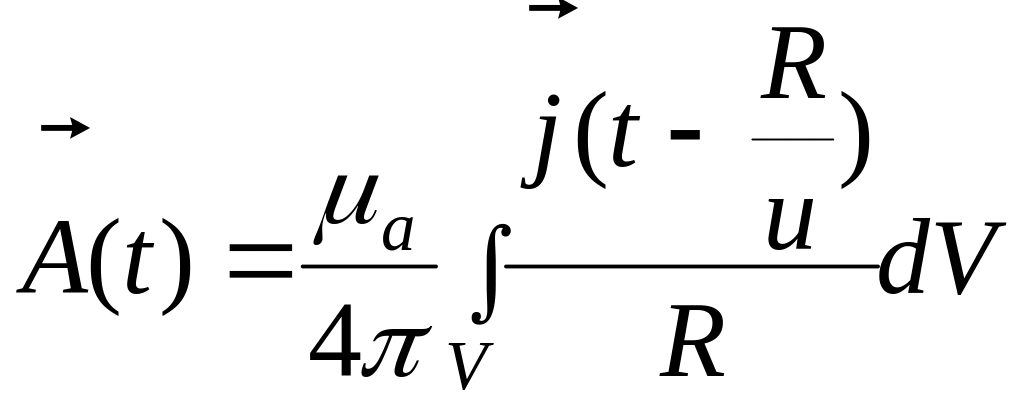где R – расстояние от начала координат, где помещен меняющийся во времени заряд , до точки наблюдения;

u – скорость распространения электромагнитного процесса;

t - момент времени, в который в точке наблюдения определяются или .

Если заряды и токи изменяются во времени, то в точке наблюдения потенциал изменится не мгновенно, а через интервал времени, за который возмущение дойдет от заряда до точки наблюдения.

Изменения свободных объемных зарядов и токов проводимости сказываются в различных точках поля не мгновенно, а спустя некоторое время , необходимое для того, чтобы электромагнитная волна прошла расстояние R. Поэтому потенциалы и называют запаздывающими потенциалами. Для вакуума скорость u равна скорости света

.

В диэлектрических средах величина скорости распространения электромагнитной энергии равна

. (5.24)