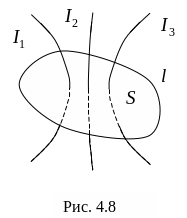
4.10. Закон полного тока в интегральной форме.

Пусть поверхность S, ограниченная контуром l, пронизывается токами I₁, I₂,… I_n (рис. 4.8). Для любой среды . Проинтегрируем это равенство по поверхности S

.

Заменим левую часть равенства по теореме Остроградского-Стокса, получим

, (4.21)

где - алгебраическая сумма токов, сцепленных с контуром интегрирования.

Полученное равенство носит название закона полного тока:

циркуляция вектора по замкнутому контуру равна сумме токов, пронизывающих этот контур, и не зависит от формы и величины контура.

Этот закон позволяет легко рассчитать симметричные поля, например, поля с осевой и цилиндрической симметрией, когда напряженность поля в каждой точке поля одинакова и может быть вынесена за знак интеграла, а интеграл приводится к простейшему виду.

Ц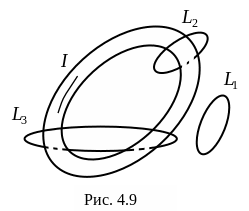 иркуляцию вектора по аналогии с электродвижущей силой называют магнитодвижущей силой.

Если контур интегрирования L₁ (рис. 4.9) не охватывает проводник, по которому течет постоянный ток, то в этом случае , а значит , т.е. контур расположен в потенциальной области поля.

Д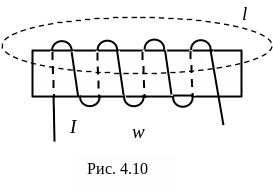 ля замкнутого контура L₂ циркуляция вектора не равна нулю, т.к. контур интегрирования охватывает проводник с током I, который является вихревой областью, и в нем .

Для контура интегрирования L₃ алгебраическая сумма токов, пронизывающих этот контур, равна нулю, поэтому .

Если ток протекает по катушке с числом витков w и контур интегрирования пронизывает все витки (рис. 4.10), то закон полного тока примет вид

. (4.22)

Расчет поля в этом случае по закону полного тока невозможен, ибо в различных точках контура интегрирования напряженность поля различная, и ее нельзя выносить за знак интеграла. В этом случае для расчета поля можно воспользоваться формулами для вектора магнитной индукции или вектор-потенциала.

П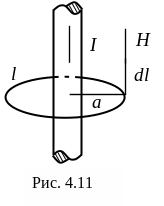 ример. Пусть магнитное поле создается постоянным током I, протекающим по бесконечно длинному проводнику (рис. 4.11). Определим напряженность магнитного поля в точке, расположенной вне провода на расстоянии а от его оси. Проведем контур l вокруг провода, тогда согласно закону полного тока,

.

Но векторы и совпадают по направлению, поэтому .

Поле, создаваемое током, протекающим по бесконечному проводу, симметрично, т.е. на одинаковом расстоянии от оси провода в плоскости, перпендикулярной проводу, величина Н одинакова. Поэтому ее можно вынести за знак интеграла

, откуда и . (4.23)

4.11. Общие сведения об индуктивности и взаимоиндуктивности.

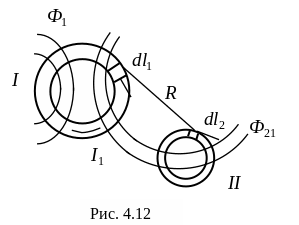
Пусть линейный ток I₁ протекает по кольцевому проводнику (контуру) (рис. 4.12). Этот ток создает магнитный поток, часть которого будет пронизывать второй контур.

,

где – коэффициент пропорциональности, называемый коэффициентом взаимоиндукции или взаимной индуктивностью. Единица измерения взаимной индуктивности – генри [Гн].

Коэффициент взаимоиндукции М определяет геометрическую структуру поля и показывает, во сколько раз изменится поток с изменением тока. Он зависит от среды, геометрических размеров и взаимного расположения контуров.

Для определения М₂₁ нужно определить поток Ф₂₁

.

, поэтому , и

. (4.24)

А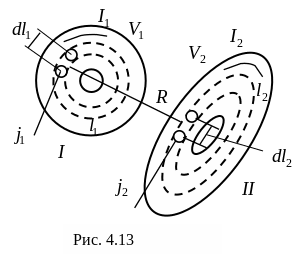 налогично получим

.

Таким образом .

Если же по контуру протекают объемные токи с плотностью и (рис. 4.13), то, следуя правилу перехода от объемного тока к линейному , , получим

. (4.25)

Если имеется один контур, то он пронизывается потоком , который вызван током , протекающим в этом же контуре, тогда собственная индуктивность контура

,

где L₁ – коэффициент пропорциональности между током I₁ в контуре и потоком, возбужденным током I₁.

Если рассматриваемый контур имеет w витков, то полученный поток будет сцепляться со всеми витками и, следовательно, потокосцепление определиться как

.

Полученные выражения для расчета М достаточно сложны, поэтому если есть возможность проще определить поток или потокосцепление Ψ, то находят эти величины, а затем определяют М или L по формулам:

, .