4.3. Закон Био-Савара.

Р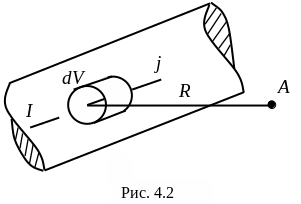 ассмотрим проводник, по которому течет постоянный ток I с плотностью (см. рис. 4.2). Определим индукцию магнитного поля в точке А.

Для этого выделим элементарный объем проводника . В объеме сосредоточен заряд . Тогда индукция магнитного поля, созданная точечным зарядом , будет

.

Внесем скалярную величину под знак векторного произведения

, но и

(4.2)

Полученное соотношение для индукции, созданной зарядами, движущимися в элементе объема, носит название закона Био-Савара. Закон Био-Савара не может быть проверен экспериментально, т.к. невозможно создать постоянный ток в отдельном изолированном элементе вне зависимости от замкнутой цепи. Но экспериментальная проверка следствий, вытекающих из данного закона, подтверждает его справедливость.

Проинтегрировав последнее соотношение по объему проводника, получим величину индукции в точке А, созданную током I.

. (4.3)

Если размеры поперечного сечения проводника малы по сравнению с его длиной и расстоянием до точки наблюдения, то такой проводник считают линейным.

Для случая протекания тока I по линейному проводнику существует формальное правило перехода в формулах от объемного тока к линейному току и наоборот

, ,

где - элемент длины проводника.

Если применить это правило к закону Био-Савара, то для случая линейного тока этот закон будет иметь следующий вид:

. (4.4)

4.4. Магнитный поток и его непрерывность.

Поток вектора магнитной индукции сквозь поверхность называют магнитным потоком.

. (4.5)

Магнитный поток измеряется в веберах (Вб). Магнитный поток величина скалярная.

Опыты показывают, что вошедший внутрь любого объема магнитный поток равен магнитному потоку, вышедшему из того же объема.

Магнитный поток сквозь замкнутую поверхность всегда равен нулю

. (4.6)

Это интегральная форма принципа непрерывности магнитного потока.

Применим теорему Остроградского (2.19)

.

Это равенство справедливо для любого объема. Следовательно,

. (4.7)

Это дифференциальная форма принципа непрерывности магнитного потока.

Таким образом, дивергенция магнитного поля равна нулю, т.е. нет ни истоков, ни стоков вектора , линии вектора всегда замкнуты.

4.5. Силы магнитного поля, действующие на движущийся заряд.

Если заряженная частица входит в магнитное поле с некоторой скоростью, то под действием сил поля траектория ее движения изменится. Как показывают опыты, сила, действующая на движущуюся заряженную частицу, направлена перпендикулярно к скорости и направлению магнитной индукции и равна .

Сила равна нулю, когда частица движется вдоль линий вектора и угол между векторами и равен нулю или 180⁰. В этом случае движение происходит по инерции, с постоянной скоростью, равной начальной скорости частицы. Сила будет наибольшей, если . В этом случае

.

Т.к. сила всегда направлена перпендикулярно к скорости , она не производит работы, не меняет абсолютной величины скорости, следовательно, не изменяет кинетическую энергию движущейся частицы. Уравнение движения частицы определяется законом Ньютона

,

где - масса частицы. Так как , то и ускорение .

Следовательно, движение будет происходить с неизменной скоростью , изменяться будет только направление вектора скорости.

Нормальное ускорение, радиус кривизны траектории и скорость движения связаны соотношением

.

1. Если , , .

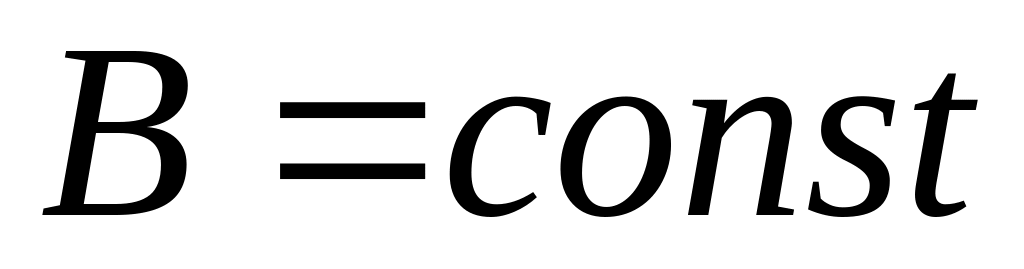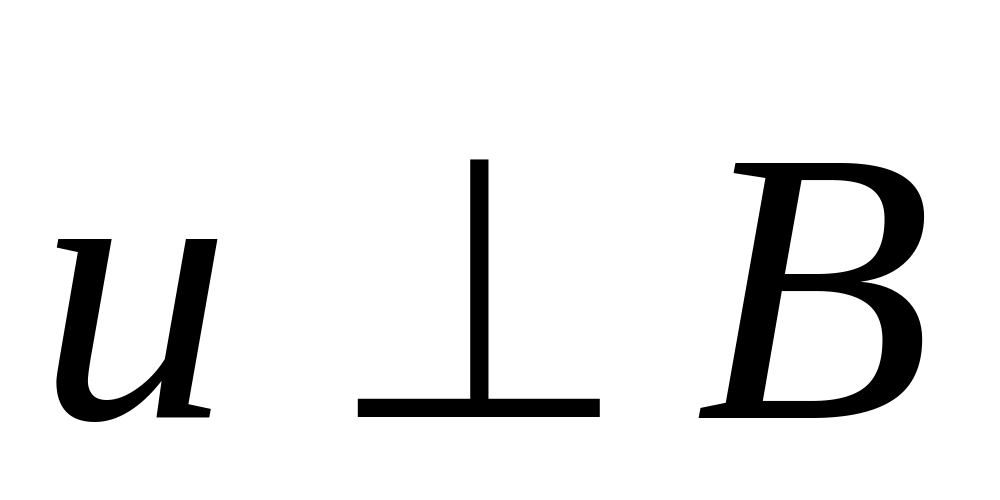При отсутствии других сил движение частицы будет происходить по окружности, лежащей в плоскости, перпендикулярной _.

_{При этом радиус окружности}

.

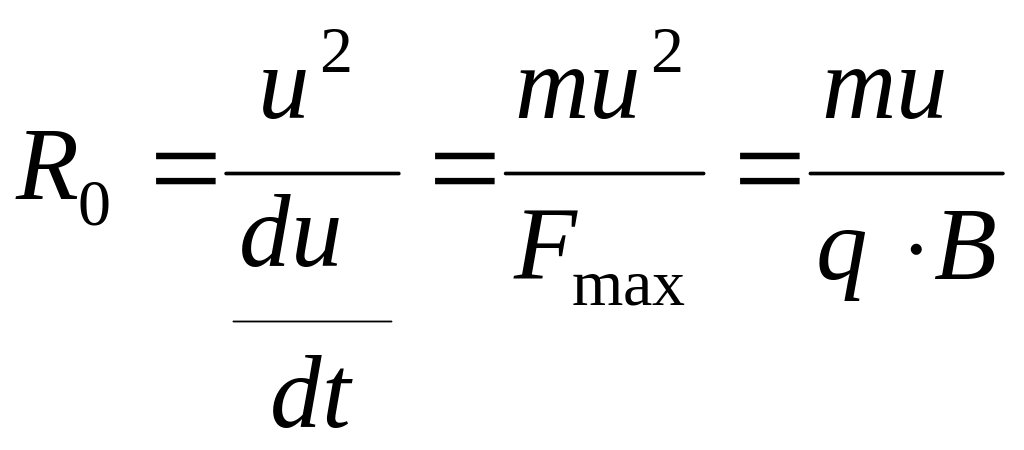
Чем больше масса m, тем больше радиус и меньше кривизна траектории.

Период вращения .

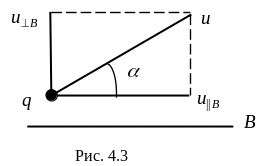
2) Если начальная скорость частицы составляет угол  с направлением вектора _{(см. рис. 4.3), то вектор скорости можно разложить на две составляющие:}

и .

Сила, действующая на частицу

.

С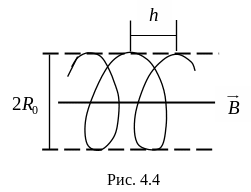 оставляющая скорости постоянна по величине и направлению. Составляющая , оставаясь постоянной по величине, изменяет свое направление под действием силы . Таким образом, движение частицы складывается из прямолинейного движения со скоростью вдоль линий вектора и равномерного движения по окружности вокруг этих линий со скоростью . Траектория результирующего движения будет винтовой линией (см. рис. 4.4).

Радиус R₀ и шаг h функции угла :

,

,

где - период вращения. Возможность управления движением частиц в магнитном поле используется в ускорителях заряженных частиц, для фокусировки электронного пучка в электронно-лучевых трубках и других устройствах.