3.3. Законы Ома и Джоуля-Ленца в дифференциальной форме.

Выделим в проводнике, по которому течет ток I, бесконечно малый цилиндр с основанием и образующей dl (см. рис. 3. 2).

Сопротивление цилиндра – ,

где - удельная проводимость проводника.

Р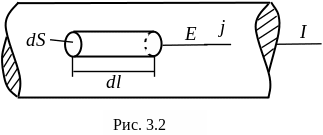 асположим этот цилиндр так, чтобы напряженность поля в нем была направлена параллельно образующей. В силу малости объема можно считать, что напряженность электрического поля одна и та же во всем элементарном объеме. Элементы эквипотенциальны, разность потенциалов между ними равна (2.28).

Закон Ома в применении к этому цилиндру

. Но , а .

Значит, , или .

Таким образом, закон Ома в дифференциальной форме имеет вид

. (3.6)

Пусть по проводнику с удельной проводимостью течет постоянный ток I. Выделим в проводнике отрезок длиной l, в котором торцы являются эквипотенциальными поверхностями. Т.к. плотность постоянного тока в различных сечениях постоянна, то

.

Разность потенциалов между эквипотенциальными поверхностями (2.27)

, (3.7)

где .

Уравнение – закон Ома в интегральной форме.

Определим энергию, выделяющуюся в элементе объема проводника (см. рис. 3.2). Если ток через основание элемента объема , а разность потенциалов между торцами рассматриваемого объема , то энергия, поглощаемая за единицу времени

.

Энергия, выделяемая в единице объема за единицу времени

(3.8)

Энергию, выделенную в единице объема за единицу времени, называют удельной мощностью.

Равенство является законом Джоуля – Ленца в дифференциальной форме.

Если в рассматриваемом объеме , то

. (3.9)

Полученное равенство – закон Джоуля – Ленца в интегральной форме.

3.4. Законы Кирхгофа

Первый закон Кирхгофа.

П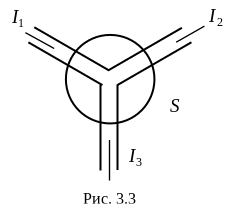 роведем замкнутую поверхность вокруг точки разветвления тока (см. рис. 3.3).

Согласно уравнению непрерывности .

Проинтегрируем это равенство по объему, ограниченному поверхностью S.

Учитывая теорему Остроградского, получим

. (3.10)

Это первый закон Кирхгофа - алгебраическая сумма токов в узле разветвления равна нулю.

Второй закон Кирхгофа.

Главным отличием поля постоянного тока является то, что для поддержания тока требуется непрерывное пополнение энергии от сторонних источников. При протекании тока происходят потери энергии, и без пополнения энергии ток быстро прекращается. Таким образом, в тех точках, где действует кроме электростатического поля, поле сторонних источников, результирующая напряженность равна геометрической сумме этих полей

,

где - напряженность электростатического поля;

- напряженность, вызванная полем стороннего источника.

Под сторонним электрическим полем понимают электрическое поле, обусловленное химическими, электрохимическими, тепловыми, термоэлектрическими процессами.

Согласно закону Ома (3.6)

. (3.11)

Это обобщение закона Ома или второй закон Кирхгофа в дифференциальной форме.

Из последнего равенства можно получить и второй закон Кирхгофа в интегральной форме.

Д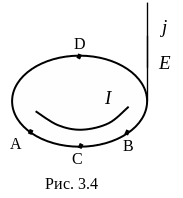 ля этого рассмотрим замкнутый контур (рис. 3.4). Направления векторов и совпадают. Пусть на участке ACB действуют сторонние источники. Тогда . Умножим обе части равенства на и возьмем интеграл по замкнутому контуру.

.

В силу потенциальности электрического поля

, поэтому

.

Разобьем интеграл на участки АСВ и BDA и, умножив числитель и знаменатель на сечение проводника, получим

,

где - электродвижущая сила стороннего поля.

Т.к. , а , то

, (3.12)

где - сопротивление цепи участка ВСА, где действует сторонняя ЭДС;

- сопротивление цепи участка ADB, где действует электростатическое поле.

Равенство (3.12) - второй закон Кирхгофа в интегральной форме.