2.3. Напряженность электрического поля.

Для определения интенсивности электрического поля, созданного уединенным зарядом q, внесем в это поле пробный заряд .

Пробным зарядом называют точечный заряд, внесение которого в поле, созданное другими зарядами, не изменяет расположение зарядов, создающих поле.

На заряд будет действовать сила , вызванная полем заряда q, которая по закону Кулона для точечных зарядов (2.2) равна

.

Напряженность поля — силовая характеристика поля, это физическая векторная величина, характеризующая возникновение сил, действующих на единицу пробного положительного заряда, помещенного в поле.

Напряженность электрического поля есть величина векторная, и обозначается буквой . Единица измерения - В/м.

, (2.3)

где - пробный заряд.

Напряженность совпадает по направлению с вектором силы .

С учетом (2.2)

, (2.4)

где - радиус-вектор, проведенный из точки расположения заряда q в точку расположения пробного заряда .

Т.к. , то модуль напряженности поля в поле точечного заряда

. (2.5)

Зная напряженность поля , можно определить силу, с которой поле действует на пробный заряд

.

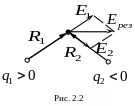
Если электрическое поле создается двумя точечными зарядами, то по принципу наложения результирующая напряженность определяется как геометрическая сумма напряженностей, создаваемых отдельными зарядами (см. рис. 2.2)

.

Пусть поле создается системой n – точечных зарядов. Применяя принцип наложения для определения результирующего значения , получим

.

2.4. Понятие об объемном, поверхностном

и линейном зарядах.

Если общий заряд q, распределен равномерно по объему V, то заряд, находящийся в единице объема, определяется как

;

где - удельная плотность объемного заряда.

Удельной плотностью объемного заряда называют заряд единицы объема.

При неравномерном распределении зарядов

.

Если заряды распределены по поверхности тела S, а толщина слоя заряда исчезающее мала по сравнению с линейными размерами поверхности, то вводится понятие поверхностной плотности заряда .

При равномерном распределении зарядов

.

При неравномерном распределении зарядов

.

Если заряды расположены на проводах, линейные размеры сечений которых достаточно малы по сравнению с длиной l и расстоянием до точек наблюдения, можно считать, что заряды распределены по осям этих проводов с некоторой линейной плотностью .

При равномерном распределении зарядов

.

При неравномерном распределении зарядов

.

2.5. Электрическое поле объемного заряда.

Пусть объем V заполнен зарядом (например, электронное облако) с удельной объемной плотностью , значение которой в каждой точке задано.

Н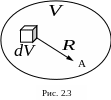 айдём в произвольной точке А напряжённость, созданную этим объёмным зарядом (рис. 2.3).

Разобьём объём на бесконечно малые элементы объёма dV.

В элементе объёма dV удельную плотность заряда можно считать величиной постоянной. Элементарный заряд можно рассматривать как точечный, а значит, напряжённость поля, созданная этим зарядом в точке наблюдения А, может быть определена по формуле (2.4)

, (2.6)

где - радиус-вектор, проведенный из элементарного заряда в точку наблюдения.

Напряжённость поля в точке А, созданная всеми зарядами, распределёнными по объёму V с удельной объёмной плотностью

. (2.7)

Интегрирование ведется по всему объёму V, где отлично от нуля.