Добавил:

darkl0rd Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Запорожский национальный технический университет

Предмет:

Основы теории колец

Файл:

otksp_STZI_press для диска

.pdf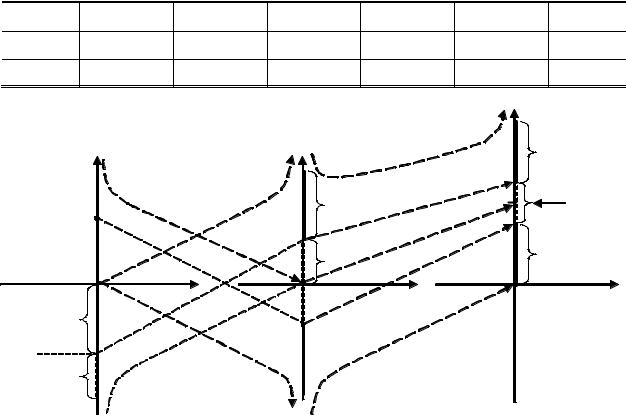

Скачиваний:

Добавлен:

13.12.2019

Размер:

17.87 Mб

Скачать

☆

<<< < Предыдущая 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 5253 / 5553 54 55 > Следующая >>>

властивість геометричної симетрії (10.104), притаманну перетворенню (10.94). На рис.10.21 показано трансформацію частотних залежностей AP для ФБ.

Таблиця 10.5 − Співвідношення між комплексними нормованими частотами ФП, ФВЧ і ЗФ

ФП		~		j0	~		− j∞	~		− j0
ФП		p		j0	j Ω		− j∞	− j Ω		− j0
ФВЧ	p =1/ p			− j∞	− j Ω		j 0	j Ω		j∞
			~
ЗФ		p		j0	jΩ1		jk∆	jΩ2		j∞
					Im p(			+j∞	Im p
~					Im p(			+j∞		СП ЗФ
~		+j∞		+j∞ +j∞						СП ЗФ
Im p		+j∞		+j∞ +j∞						jΩ2
						СП ФВЧ		jk∆		jΩ2
~					(	СП ФВЧ		jk∆		СЗ ЗФ
jΩ					(					jΩ1
					jΩ					jΩ1
j0			~		+j0	СЗ ФВЧ				j0 СП ЗФ
	−j0		~				(
	−j0		Re p				(
СП ФНЧ						(	Re p			Re p
		~			− jΩ
		~
СЗ ФНЧ		− jΩ
СЗ ФНЧ
		−j∞		−j∞	−j∞
Площина	~	ФНЧ			(	ФВЧ		Площина		p ЗФ
Площина	p	ФНЧ		Площина p		ФВЧ		Площина		p ЗФ

Рисунок 10.20 – Перетворення частотних діапазонів ФНЧ−ФВЧ і ФВЧ−ЗФ

Щоб визначити ОПФ ЗФ, слід від вимог до частотних характеристик ослаблення ЗФ спочатку перейти до вимог AP ФВЧ, а потім – до ФП (ФНЧ).

Вихідними даними для розрахунку ЗФ є смуга затримання частота ω0 та співвідношення, аналогічні нерівностям (10.7):

AP (ω∆1) = AP (ω∆2 ) ≤ A∆ ;

AP (ωs1) = AP (ωs2 ) ≥ As .

∆ωз, центральна

(10.122)

Умови (10.122) ЗФ аналогічні умовам (10.105) для СФ, але відрізняються співвідношеннями між частотами: ω∆1 < ωs1 < ωs2 < ω∆2 .

З двох значень частоти ωsi ( ω∆i ), як правило, відоме тільки одне. Тому, виходячи з геометричної симетрії частотної залежності AP (10.104), за задани-

ми частотами обчислюють симетричні частоти (наприклад: ω	∆2	=ω2	/ω	∆1	;
	∆2	0		∆1

Основи теорії кіл, сигналів та процесів в СТЗІ. Ч.1

521

ωs1 =ω02 /ωs2 ). Далі від вимог (10.122) переходять до співвідношень щодо ФВЧ для тих самих значень ослаблення:

	(	) ≤ A ;
	A (ω	) ≤ A ;	(10.123)
	P (∆	∆	(10.123)
	AP (ωs ) ≥ As ,
	(
де	ω∆ = ω∆2 −ω∆1;		(10.124)
де	(	−ωs1.	(10.124)
	ωs = ωs2	−ωs1.

Для ФБ порядок ФВЧ

n ≥ n*

( n

– ціле округлене

n ) визначається на

підставі формули (10.85) за умови рівностей у системі (10.123):

lg(100,1As −1) −lg(100,1A∆

−1)

Ω

(

∆

(10.125)

(

n =

2lg(Ω∆ /

Ωs )

Ωs

ωs

Оскільки гранична частота ФВЧ, яка визначається на рівні 3 дБ, збігається

із смугою затримання ЗФ, її можна знайти, виходячи з виразу (10.89):

∆ω

(

(10

0,1A

1/ 2n*

(

(10

0,1A

1/ 2n*

(10.126)

=ω

∆

−1)

=ω

−1)

гр

де n* – дробове число (10.125).

Оскільки порядки ФНЧ і ФВЧ однакові, можна записати ОПФ ФП, використовуючи вираз (10.38):

~		1
HU ( p) =
HU ( p) =	n	~	~
	Π	( p	− pk )
	k =1

де нормовані корені ФНЧ Баттерворта

(10.127)

обчислюють за формулою

(10.109).

Для ФЧ порядок n ФВЧ визначають, виходячи з виразів (10.67), (10.81):

n≥

Arch(

100,1As −1/ε)

(10.128)

(

Arch (1/ Ωs )

де Ωs =ωs /

ω∆ – нормована частота ФВЧ, яку розраховують за формулою

(

–

згідно

системою

(10.124); коефіцієнт

(10.92); частоти ω∆

ωs

нерівномірності ослаблення ε – за формулою (10.66).

З огляду на збіг порядків ФВЧ і ФП на підставі співвідношення (10.80),

ОПФ ФП можна записати у вигляді:

HU ( p) =

Π ( p − pk )

k =1

де коефіцієнт kR =1/(2n−1ε) (загалом kR може мати довільне значення). При kR =1 аналітичний вираз ОПФ ФЧ збігається з (10.127), але для ФЧ

~ = −∆~ + Ω~

нормовані корені pk k j k визначатимуться з урахуванням формул (10.71) і (10.72) відповідно до співвідношення (10.111).

522	Ю.О.Коваль, І.О.Милютченко, А.М.Олейніков та ін.

AP (Ω)

3 дБ

A∆

− Ω

−

−Ω

∆

Ω

∆

Ω

−ωs

−ω∆

ω∆

ωгр

ωs

(

−ωгр

AP (Ω)

(

3 дБ ∆ω3дБ

A∆

(

−1

(

−Ω∆

−Ω

Ωs

(

1 Ω∆

(

−ω∆

−ωгр

−ωs

ωs

ωгр

ω∆

AP (Ω)

Ω

(

Ω

ω(

Ωs1

3 дБ			∆ωз	Ωs2
3 дБ				Ωгр2
A∆				Ωгр2
A∆
0	Ω∆1		k∆	Ω∆2	Ω
0	Ωгр1	ω∆1	ωs1 ω0	ω∆2	ω
	Ωгр1	ωгр1	ωs2	ωгр2
		ωгр1	ωs2	ωгр2

Рисунок 10.21 – Перетворення частотних характеристик ослаблення ФНЧ−ФВЧ і ФВЧ−ЗФ для ФБ

Перехід від ОПФ ФП (10.127) до нормованої ОПФ ЗФ потребує встановлення відповідності між нормованими коренями ФП і ЗФ згідно із співвідношенням (10.118). Розв’язання рівняння (10.118) відносно p дає:

Основи теорії кіл, сигналів та процесів в СТЗІ. Ч.1

523

~	2	2	~	= 0 ,
p p		− p + k∆ p		= 0 ,
			p =		1
			p =		~
					2 p

або	p2	1		p	+ k∆2	= 0,	звідки:
		−
		−	~
			p
±	1	− k 2 .					(10.129)
	~ 2		∆
	4 p

	За умови	p = jΩ	~	~
	За умови	p = jΩ	для двох комплексно-спряжених значень p	= jΩ і
~	~
p	= − jΩ, виходячи з виразу (10.129), можна встановити безпосередній зв’язок

~
між нормованими частотами ФП Ω і ЗФ Ω (опускаючи знак «мінус» перед ко-
ренем, що забезпечує додатне значення частоти Ω):
1	1	(10.130)
Ω = ± ~ +	~ 2 + k∆2 .	(10.130)
2Ω	4Ω	~
Як і у випадку СФ, знайдену	нормовану ОПФ ФП	~
Як і у випадку СФ, знайдену	нормовану ОПФ ФП	HU ( p) (10.127)

доцільно представити у вигляді (10.112) для парного n або (10.113), якщо n −

	~	(1)	~	− ОПФ
непарне. За умови непарного n з функції HU ( p)		виділяється HU	( p)	− ОПФ
~	~
ланки першого порядку з коренем p	= −∆, котра перетворюється на нормовану

ОПФ ЗФ з двома нулями і полюсами, які відповідно є комплексно-спряженими:

(2)

(1)

)

p2 + k∆2

( p) = HU

( p)

p%= p /( p2

+k2 )

= k

∆

p + ∆

+ p / ∆ + k∆

p= p

/( p

+k∆ )

де k =1/ ∆ =1/

ОПФ

(2)

i -х ланок другого

порядку

ФП,

виділених

функції

HU i

( p)

перетворюються у нормовану ОПФ ЗФ чет-

(10.112), з коренями pi = −∆i ± jΩi

вертого порядку.

Якщо

ОПФ

однієї

ланки

другого

порядку представити

вигляді

(2)

HU i

( p) =

і виконати перетворення для кожного з комплексно-

~ −

p − p

спряжених коренів окремо, виходять ланки ЗФ з ОПФ другого порядку:

p2 + k∆2

= −ki

p2 + k∆2

= −

p% − p%

2 −

( p − p )

(

p − p

p / p

2 )

= p /( p +k∆ )

∆

Аналогічно

p2 + k∆2

= −

= −k*

% − %*

2 −

i ( p − p

)

(

p − p

4 )

p pi

p / pi

k∆

p= p /( p

+k∆ )

де ki =1/

;

p1,3

, а також

p2,4

утворюють комплекс-

1/ pi , причому

но-спряжені пари подібно перетворенням щодо СФ. Тому достатньо визначати тільки корені p1 і p2 , скориставшись формулою (10.129).

З урахуванням зроблених перетворень нормовану ОПФ ланки четвертого порядку ЗФ можна записати у вигляді:

524	Ю.О.Коваль, І.О.Милютченко, А.М.Олейніков та ін.

(2)					1				p2	+ k∆2		p2	+ k∆2
(2)					1				p2	+ k∆2		p2	+ k∆2
HU ( p) = HU i	( p)		2 2	=										, (10.131)
HU ( p) = HU i	( p)		2 2	=			2							, (10.131)
	%	p= p /( p	+k∆ )		%				( p − p )(p − p		)( p − p )(p − p )
		%				pi		1		3	2		4

де 1/ p%i 2 = kik =1/(∆%i2 + Ω% i2 ) ,

тобто як добуток двох ОПФ ланок другого порядку з двома комплексноспряженими полюсами і двома комплексно-спряженими нулями. Така форма найбільш прийнятна при каскадній реалізації фільтра.

Враховуючи співвідношення (10.79), знаменник у виразі (10.131) слід представити у вигляді поліномів відносно p . Денормування ОПФ ЗФ

здійснюється підстановкою (10.119):
HU ( p) = HU ( p)	p=p / ∆ωз .		(10.132)
			(10.132)

Приклад 10.5. Визначити ОПФ ЗФ Чебишова за такими вимогами: центральна
частота ω = 424,279 103 рад/с, смуга затримання		∆ω =161,66 103	рад/с. На
0		3

частоті ωs1 = 404,75 103 рад/с ослаблення за потужністю не має бути меншим 24 дБ, на частоті ω∆2 =512,74 103 рад/с – не повинне перевищувати 0,97 дБ.

Розв’язання. Скориставшись властивістю геометричної симетрії частотної залежності AP (10.104), визначимо частоти ω∆1 і ωs2 :

ω∆1	=		ω02	=	424,2792 106	= 351,08	103 рад	;
		ω∆2			512,74 103
							с
ωs2	=		ω02	=	424,2792 106	= 444,75	103 рад .
			ωs1		404,75 103
							с

За принципом збереження довжини частотного інтервалу визначимо частоти

ω∆ і ωs (10.124) ФВЧ:

ω(∆ = ω∆2 −ω∆1 = 512,74 103 −351,08 103 =161,66 103 радс

( ω∆ така ж сама, як і смуга затримання);

ω(s = ωs2 −ωs1 = 444,75 103 −404,75 103 = 40 103 радс .

За нормованою частотою ФВЧ Ωs =ω(s /ω(∆ обчислимо нормовану частоту ФП:

Ω% s =1/ Ω( s =160,66 103 / 40 103 = 4,0415 радс .

За формулами (10.66) і (10.67) розрахуємо ε і n ФП:

ε = 100,1Α∆ −1 = 100,1 0,97 −1 = 0,500259 ;

n ≥	Arch(	100,1As	−1/ε)	=	Arch( 100,1 24 −1/ 0,500259)	=1,9992 . Нехай
n ≥		%		=	Arch 4,0415	=1,9992 . Нехай
		Arch Ωs			Arch 4,0415

Оскільки значення ε і n ФП збіглися з результатами прикладу ристаємось отриманими значеннями нормованих коренів:

~	~ ~	± j0,899454 ;	~	2	=1,118035 .

p1, 2	= −∆ ± jΩ = −0,555893		p1

n = 2 .

6.4, ско-

Основи теорії кіл, сигналів та процесів в СТЗІ. Ч.1

525

На підставі виразу (10.129) обчислимо нормовані корені ЗФ:

p1 = −0,210778 + j2,24152 = −∆1 +jΩ1;

p2 = −0,286428 −j3,046015 = −∆2 −jΩ2 ;

p3 = −0,210778 − j2,24152 = −∆1 −jΩ1;

p4 = −0,286428 + j3,046015 = −∆2 + jΩ2 .

Нормована ОПФ ЗФ, виходячи з виразу (10.80) за умови kR =1 згідно з форму-

лами (10.131) і (10.79), набуває вигляду:

p2 + k∆2

HU ( p) =

;

+ 2∆1 p + ∆1

+Ω1

+ 2∆2 p + ∆2

+Ω2

k∆ =ω0 / ∆ωз = 2,624514 , або після підстановки числових значень

HU ( p) = 0,894426

p2 +6,888076

p2 +0,57945 p +9,36215

+0,421556 p +5,068838

Денормовану ОПФ ЗФ отримаємо, використовуючи вираз (10.132):

За знайденою ОПФ визначимо частотну залежність ослаблення (10.1), яка зображена на рис.10.22.

AP (ω), дБ

20 AP(404750) = 24,031 дБ AP(444750) = 24,057 дБ

10					AP(351080) = 0,98 дБ
0,97					AP(512740) = 1,053 дБ
		4		6	ω×
0	3		5			5	рад/с
					10
Рисунок 10.22 – Частотна залежність ЗФ порядку n = 4
Незначні розбіжності		Ap	із заданими значеннями ослаблення A∆ обумовлені

недостатньою точністю обчислення коренів, вплив якої помітний, оскільки розрахований порядок фільтра n (1,9992) і прийнятий (2), дещо різняться. Щоб усунути вказані розбіжності, слід розраховувати значення коренів з більшою точністю (як для ФП, так і ЗФ).

10.9 Синтез фільтрів на операційних підсилювачах

Вище у даному розділі розглянуто перший етап синтезу кола – визначення ОПФ, яка задовольняє певним вимогам до частотних характеристик кола і відповідає умовам фізичної реалізації. Не менш важливими є другий і третій етапи

– це задачі структурного і параметричного синтезу кола. Розв’язання цих задач за допомогою схем з ОП ілюструє наступний приклад.

Приклад 10.6. Знайти структуру та параметри елементів кола, за допомогою яких можна реалізувати ОПФ СФ Чебишова, отриману в прикладі 10.4.

526	Ю.О.Коваль, І.О.Милютченко, А.М.Олейніков та ін.

Розв’язання. У прикладі 10.4 отримано ОПФ СФ четвертого порядку у вигляді:

HU ( p) = H1( p)H2 ( p) =

Πω p		Πω p
=p2 +0,532336 Πω p +103,350727 Πω2 × p2 +0,57945Πω p +122,454527 Πω2 .
Підставивши значення смуги пропускання Πω = 40 103 рад/с, матимемо:
H1( p) =	40 103 p			;	(10.133)
H1( p) =				;	(10.133)
p2 + 21293,44 p +1,6536116 1011
H2 ( p) =	40 103 p		.		(10.134)
H2 ( p) =	+ 23178 p +1,9592724 1011		.		(10.134)
p2	+ 23178 p +1,9592724 1011
Оскільки функція HU ( p)	дорівнює добутку H1( p) ×H2 ( p) , вона може бути
реалізована у вигляді каскадного з’єднання чотириполюсників (рис. 10.23).
Zвх2
H1 ( p)	H 2 ( p)				H n ( p)

Zвих1

Рисунок 10.23 – Каскадне з’єднання чотириполюсників

Загалом існує два способи каскадної реалізації:

1) каскадно-узгоджена, коли вхідний опір наступного каскаду збігається з вихідним опором попереднього ( Zвхn = Zвих(n−1) ); цей спосіб застосовують при

реалізації мостовими або східчастими реактивними чотириполюсниками; 2) каскадно-розв’язана, коли вхідний опір наступного каскаду значно більший

вихідного опору попереднього ( Zвхn >> Zвих(n−1) ); здійснюється за допомогою схем з

ОП (активних R, C фільтрів), у яких вхідний і вихідний опір відрізняються на декілька порядків (див. підрозд. 5.8).

З аналізу функцій H1( p) і H2 ( p) видно, що вони відповідають ланкам друго-

го порядку типу СФ (див. підрозд.5.6), кожну з яких можна реалізувати за допомогою активного R, C фільтра. Згідно з другим способом реалізації ОПФ СФ четвертого порядку забезпечується каскадним з’єднанням двох активних ланок другого порядку.

Користуючись відомою методикою (див. приклад 8.10, а також підрозд.5.8), знайдемо ОПФ активного фільтра другого порядку (рис.10.24).

ОПФ фільтра визначимо за формулою:

H1( p) = U4 ( p) = ∆14,43 ,

U1( p) ∆11,43

яка містить відношення алгебраїчних доповнень матриці операторних провідностей кола:

Основи теорії кіл, сигналів та процесів в СТЗІ. Ч.1

527

	1	2			3			4
1	G	−G			0			0
(Y ( p))= 2	1	1		− pC2			− pC1
(Y ( p))= 2	−G1	G1 +G2 + pC1 + pC2		− pC2			− pC1		.
3	0	− pC	2	G	+ pC	2	−G
	0		2	3		2	G	3
4	0	− pC		−G			G	+ pC
			1		3		3	1

		C1		R3
			C2	R3
1	R1	2	C2		4
1		2	3	∞	4
				∞
U1( p)		R2			U 4 ( p)
		R2			U 4 ( p)

Рисунок 10.24 − Схема активного СФ другого порядку

Відповідні алгебраїчні доповнення отримаємо, враховуючи відомі правила визначення знаків (див. підрозд. 5.8) та викреслюючи у чисельнику і знаменнику 1 і 4-й рядки, 4 і 3-й стовпці – у чисельнику та 1 і 3-й – у знаменнику:

∆	= −pG C	2	;		∆		= p2C C		2	+ pG (C +C				) +G (G +G ) .
14,43	1	2			11,43		1		2		3	1	2	3		1	2
Остаточно матимемо:								pG1C2
	H1( p) = −							pG1C2							.		(10.135)
	H1( p) = −			p2C C		2	+ pG (C			+C	)	+G (G		+G )	.		(10.135)
					1	2	3		1	2		3	1	2

Переходячи від провідностей до опорів і вважаючи для спрощення однаковими значення ємностей C1 = C2 = C , отримаємо:

H1( p) = −		p / R1C					.	(10.136)
H1( p) = −	p2 + 2 p / R C +(R + R ) / R R R C2						.	(10.136)
	3	1	2	1	1	3

З рівності коефіцієнтів при однакових степенях p у виразах для ОПФ (10.133) і (10.136), виходить система рівнянь для визначення елементів першої ланки СФ:

		(1)		C	(1)	= 4 10	4	;
1/ R				C		= 4 10		;
	1					= 21293,44;				(10.137)
2 / R3(1)C(1)						= 21293,44;			(C(1) )2	(10.137)
(R(1)			+ R(1) ) / R(1) R(1) R(1)						(C(1) )2	=1,6536116 1011 ,
	1				2	1		2 3

де верхніми індексами позначено приналежність елементів до першої ланки. Оскільки в системі (10.137) кількість невідомих більше кількості рівнянь, слід

задатися значенням певного параметра, виходячи з додаткових умов, пов’язаних з конструктивною чи схемною реалізацією, типовою схемою увімкнення каскаду тощо.

528	Ю.О.Коваль, І.О.Милютченко, А.М.Олейніков та ін.

Нехай С1(1) = С2(1) = С(1) =100 пФ. Тоді з першого рівняння системи (10.137): R1(1) = 250 кОм, з другого – R3(1) = 939,256 кОм, з третього – R2(1) = 645,5 Ом.

Аналогічно, прирівнюючи коефіцієнти при однакових степенях p у виразах для ОПФ (10.134) і (10.136), складемо систему рівнянь для другої ланки:

		(2)		C	(2)	= 4 10		4	;
1/ R				C		= 4 10			;
	1													(10.138)
2 / R3(2)C(2) = 23178;										(C(2) )2 =1,9592724 1011 .				(10.138)
(R(2)			+ R(2) ) / R(2) R(2) R(2)							(C(2) )2 =1,9592724 1011 .
	1				2		1		2 3
Якщо вважати (з метою уніфікації елементів), що С(1)											= С	(1)	= С(2)	= С(2) , з
										1		2	1	2
системи (10.138) виходить: R(2)							= 250 кОм;			R(2) = 593,2 Ом;	R(2)	=862,387 кОм.
						1				2	3

10.10 Запитання та завдання для самоперевірки

іконтролю засвоєння знань

1.З яких етапів складається розв’язання задачі синтезу електричного кола? Пояснити зміст кожного етапу.

2.Який зв’язок існує між АКХ кола та ослабленням кола за потужністю? Які вимоги ставлять до частотної залежності ослаблення?

3.Які фільтри називають поліномними?

4.Пояснити особливості частотних характеристик фільтрів Баттерворта. Зобразити якісно графіки цих характеристик для ФНЧ Баттерворта різних порядків.

5.Як розташовані на комплексній площині корені полінома Баттерворта?

6.Які особливості мають частотні характеристики фільтрів Чебишова? Зобразити якісно АЧХ ФВЧ Чебишова другого і третього порядків.

7.Які особливості мають поліноми Чебишова? Розрахувати коефіцієнти полінома Чебишова 11-го порядку.

8.Чим відрізняються ЧХ фільтрів Чебишова і Золотарьова?

9.У чому відмінність синтезу ФНЧ від синтезу фільтрів інших типів? Пояснити поняття «фільтр-прототип».

10.Пояснити, як здійснюється перетворення частотних діапазонів ФНЧ-ФВЧ. Яке співвідношення пов’язує комплексні нормовані частоти ФНЧ і ФВЧ?

11.Пояснити, як здійснюється перетворення частотних діапазонів ФНЧ-СФ. У чому полягає принцип збереження довжини частотного інтервалу?

12.Як використовують властивість геометричної симетрії частотної характеристики для синтезу смугового фільтра?

13.Визначити ОПФ ФНЧ Баттерворта, якщо на частоті 750 Гц ослаблення за

потужністю AP ( f ) не повинне перевищувати 2 дБ, а на частоті 1600 Гц – бути мен-

шим 20 дБ.

Відповідь:

HU ( p) =	2526,62 104		×	2526,62	104	.
	p2 +3847,32 p + 2526,62	104		p2 +9288,06 p +	2526,62 104

14. Пояснити, чи можна реалізувати ОПФ, знайдену у завданні 13, за допомогою двох каскадно-з’єднаних активних ланок другого порядку (рис.8.7). Знайти значення елементів цих ланок, якщо для кожної з них R1 = R2 = R3 = 51 кОм.


Основи теорії кіл, сигналів та процесів в СТЗІ. Ч.1	529

Відповідь: С1(1) =15,3 нФ; С2(1) =1 нФ; С1(2) = 6,33 нФ; С2(1) = 2,4 нФ.

15. Визначити ОПФ ФВЧ Баттерворта, якщо на частоті 20 кГц ослаблення за потужністю AP ( f ) не повинне перевищувати 1 дБ, а на частоті 4500 Гц – бути меншим 20 дБ.

Відповідь:	HU ( p) =		p2	.
		p2	+12,58 104 p +79,6 108

16. Користуючись відомою методикою (див. приклад 8.10), знайти ОПФ активного фільтра (рис.10.25) та порівняти з результатом завдання 15. Реалізувати ОПФ, знайдену у завданні 15, за допомогою активного ФВЧ. Знайти значення елементів активного фільтра, поклавши C1 = C2 = C3 =1 нФ.

Відповідь: R1 = 5,27 кОм; R2 = 23,85 кОм.
		C2			R2
	C1		C3		R2
1	C1	2	C3	3	∞	4
1		2		3		4

U1( p)		R1				U 4 ( p)

Рисунок 10.25 − Схема активного ФВЧ другого порядку

17. Реалізувати ОПФ фільтра Чебишова (див. приклад 10.3) за допомогою диференціювальної ланки першого порядку (рис.7.13, а) і активної ланки другого порядку (рис.10.25). Знайти значення опорів цих ланок, поклавши

C = C1 = C2 = C3 = 2 нФ.

Відповідь: R = 50 кОм; R1 =16,7 кОм; R2 = 600 кОм.

f0 = 40 кГц;

18. Визначити ОПФ

СФ Баттерворта

за такими

даними:

f∆1 = 35 кГц; fs2 = 54 кГц;

A∆ =1 дБ;

=17 дБ. Знайти порядок та граничну час-

тоту фільтра-прототипу.

Відповідь: n = 4 ;

fгр =12,68 кГц;

HU ( p) =

6347,4348 106 p2

p4 +60980 p3 +69512,9

106 p2 +3851,83 1012 p +3989,88 1018

6347,4348 106 p2

+147215,69 p

+69512,9 10

p +3989,88

9298,95 10

530	Ю.О.Коваль, І.О.Милютченко, А.М.Олейніков та ін.

<<< < Предыдущая 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 5253 / 5553 54 55 > Следующая >>>