Правильное отсечение в алгоритме р.Гомори

Итак, в основу метода отсечения положено последовательное "усечение" исходного множества D с целью построения части выпуклой линейной оболочки в области максимума ЦФ.

В этой связи ясно, что любая задача ЛП(k+1) в последовательности задач {ЛП(k)} отличается от задачи ЛП(k) некоторым ограничением, которое должно обладать соответствующими свойствами.

Рассмотрим две эти задачи.

Определение правильного отсечения

Ограничение

(5)

называется правильным отсечением, если это ограничение удовлетворяет следующим требованиям:

1. Пусть - оптимальное решение задачи ЛП(k), имеющеене целыекоординаты. Тогда:, то есть, ограничение (5) не выполняется (условиеотсечения);

2. Пусть - любоецелочисленноерешение задачи ЛП(k). Тогда: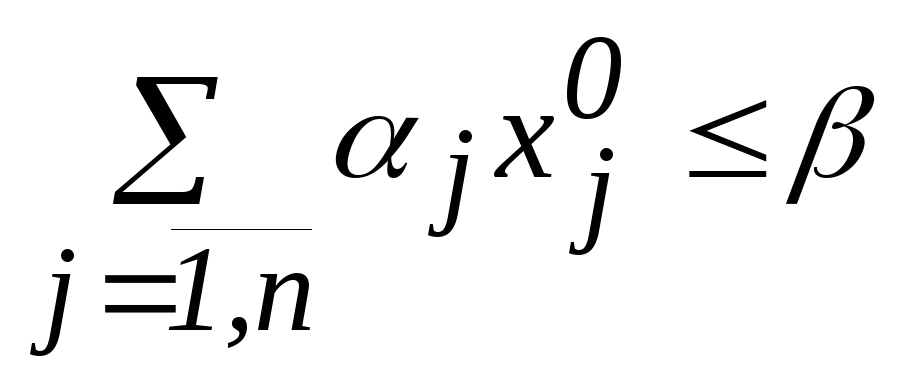, то есть, ограничение (5) выполняется (условиеправильности);

Линейный вид ограничения (5) позволяет использовать методы ЛП.

Как по решению задачи ЛП(k) построить ограничение - правильное отсечение для того, чтобы сформировать новую задачу последовательности ЛП(k+1)?

Предварительно нужно строго определить целую и дробную часть числа.

Целую часть произвольного вещественного числа   обозначим  []:

[] - наибольшее целое число, не превосходящее.

Дробной частью произвольного вещественного числа   называется число {}:  {}=- [].

Пример: {7/3}=1/3, {-7/3}=2/3.

Решим задачу ЛП(0) - исходную задачу (1)-(3), игнорируя требование целочисленности (4).

Пусть -  оптимальное решение этой задачи. Пусть, далее, для определенности:

-  номера базисных переменных;

-  номера свободных переменных;

Если все координаты решения  - целые, то получено оптимальное решение исходной ЛЦП-задачи. В противном случае решение нужно продолжить.

Рассмотрим оптимальную симплекс-таблицу решенной задачи.

……………………………………………………………….

Пусть  l– индекс некоторой нецелой координаты:

.

Выпишем    l-е  уравнение (l-я строка симплекс-таблицы):

. (6)

А теперь рассмотрим следующее выражение:

, где

y_l – некоторая переменная:

. (7)

Относительно этого выражения справедлива следующая теорема.

Теорема о правильном отсечении.

Если - любое целочисленное решение (не обязательно опорное) задачи (1)-(3), т.е. допустимое решение ЛЦП-задачи, то:

y_l  0, y_l  - целое число.

Доказательство. Перепишем (6):

.

,

.

Но  и- целые, т.е., правая часть – целое число. Следовательно, и левая часть – такжецелое число.

Пусть теперь y_l < 0(от противного). То есть:

.

Но , аи. Значит, имеет место:, чего не может быть, т.к.- целое число. Полученное противоречие говорит о неправомерности предположения о том, чтоy_l < 0. Теорема доказана.

Следствие теоремы о правильном отсечении.

Любое оптимальное опорное решение ЛП-задачи (1)-(3), имеющее нецелую координату, не удовлетворяет условию:

(*)

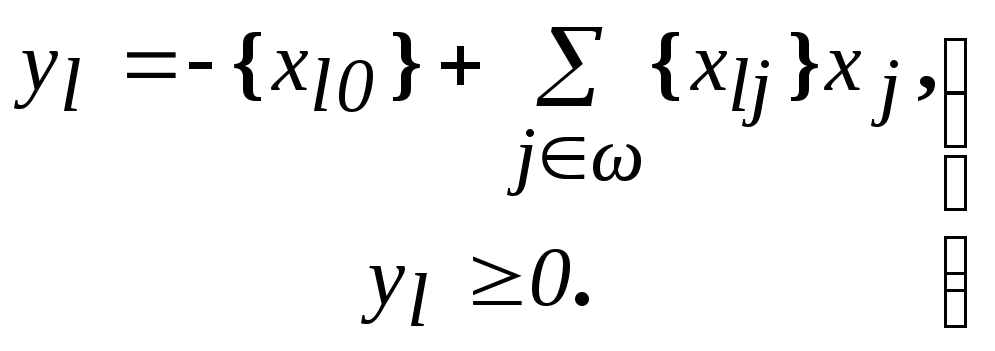Доказательство. Действительно, если - не целое, то по определению. Но все свободные переменные в опорном решении имеют нулевое значение. То есть,. Следовательно, ограничение (*) не выполняется, что и требовалось доказать.

Итак, по решению некоторой задачи можно построить правильное отсечение.