7

2 ЛЦП-введение.doc

Целочисленное программирование

ЦП – один из важных и наиболее трудных разделов МП. Весьма значительный круг задач планирования, масса технических задач, сводится к выбору лучших параметров из некоторой дискретной совокупности заданных величин. Грубо говоря, это те же задачи МП:

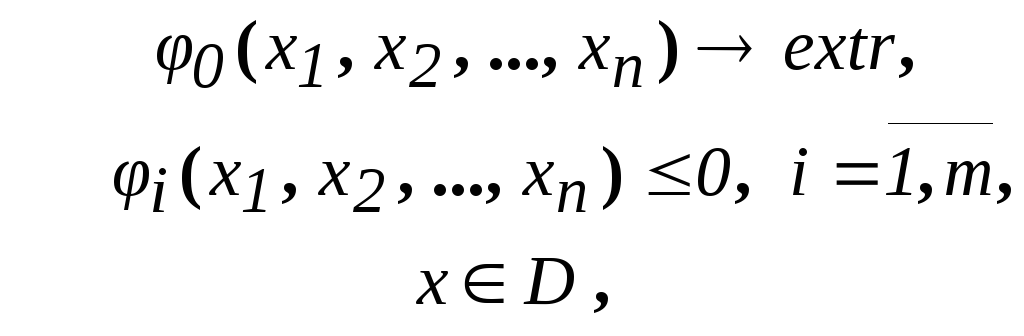
с единственным отличием – дискретной областью определения всех или некоторых параметров.

Несмотря на кажущуюся простоту постановки задач ЦП, математические трудности, возникающие при их анализе, могут быть весьма значительными.

Достаточно вспомнить Великую Теорему Пьера Ферма (17-й век, профессия – юрист). Суть этой теоремы сводится к следующему.

Диофантово уравнение , где n – целое число, большее двух, не имеет решения в целых положительных числах.

Эта теорема может быть сформулирована, как следующая задача целочисленного программирования:

,

; ; ; ,

Так вот, любой метод, позволяющий решить эту задачу в обозримое время, будет конструктивным методом анализа теоремы Ферма:

Если min ЦФ>0, то теорема доказана;

Если min ЦФ=0, то утверждение теоремы Ферма опровергнуто.

Математические модели целочисленного программирования

Главным образом в целочисленном программировании исследуется модель следующего вида:

, (1)

, (2)

, (3)

x_j – целые . (4)

При   n=n₁  имеет место задача  целочисленного программирования;

При  n>n₁ -  задача  частично-целочисленного программи-рования.

Условие целочисленности (4) может быть заменено требованием дискретности:

,

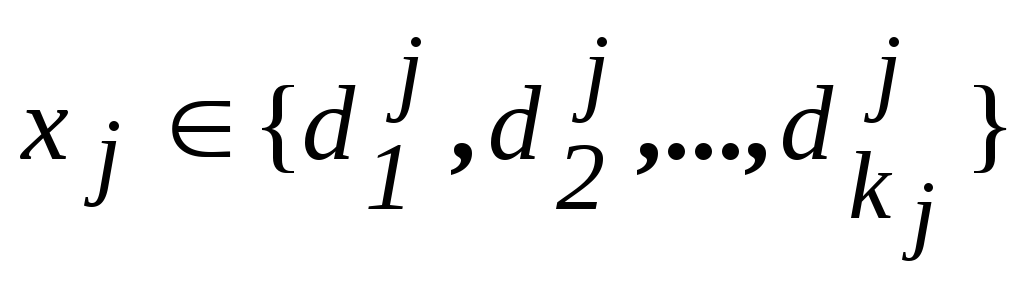При  n=n₁  имеет место задача  дискретного программирования;

При  n>n₁ -  задача  частично-дискретного программиро-вания.

Частным случаем задачи линейного целочисленного программирования (ЛЦП) является задача линейного целочисленного программирования с булевыми переменными ЛЦП(б):

,

,

x_j {0,1} .

Это – очень важный класс задач. Достаточно сказать, что если заранее установлены пределы возможных значений переменных, любая задача дискретного или целочисленного программирования может быть сведена к ЛЦП(б) – задаче.

Сведение к задаче лцп(б) задачи дискретного программирования

Пусть имеется задача дискретного программирования:

,

,

,.

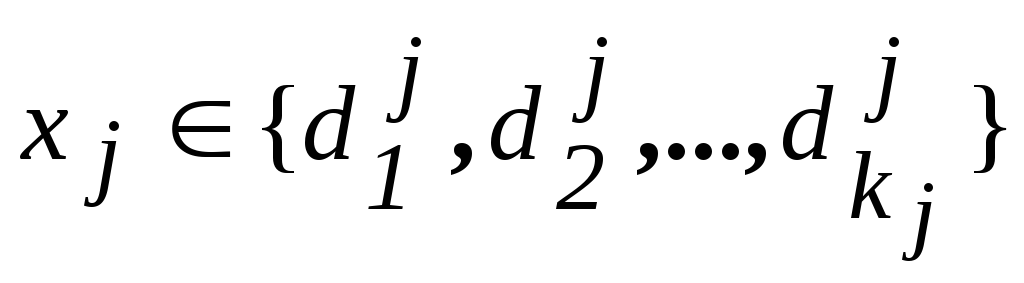1. Введем булевы переменные (по одной переменной на каждое дискретное значение):

, , , .

2. Наложим на эти переменные требование:

, (). (*)

3.  Произведем замену переменных:

Учитывая  (*) , всегда будет иметь место:

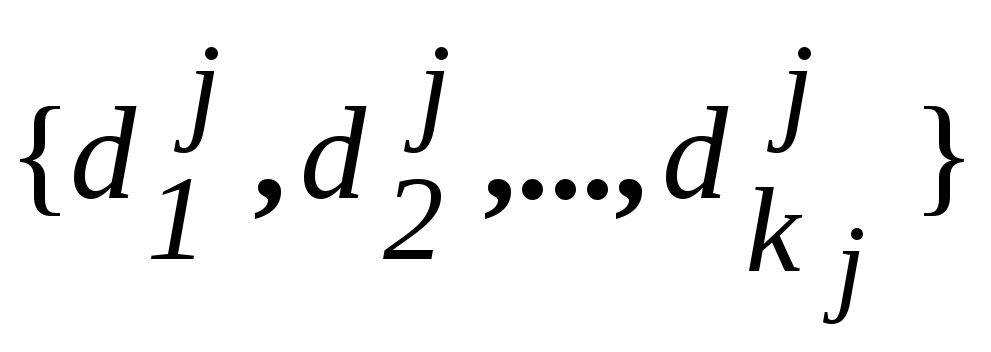 - то, что и требуется. Окончательно модель приобретает вид:

, ,

, , .

Сведение к задаче лцп(б) задачи дискретного нелинейного программирования

Отдельные нелинейные задачи с дискретной областью определения переменных могут быть сведены к виду ЛЦП(б)-задачи.

Пусть имеется задача, в которой , .

Пусть, далее, в целевой функции или где-нибудь в ограничениях фигурирует нелинейная функция . Эта функция, в частности, может быть задана таблично.



То есть:

. (*)

1. Введем булевы переменные:

, , , .

2. Представим 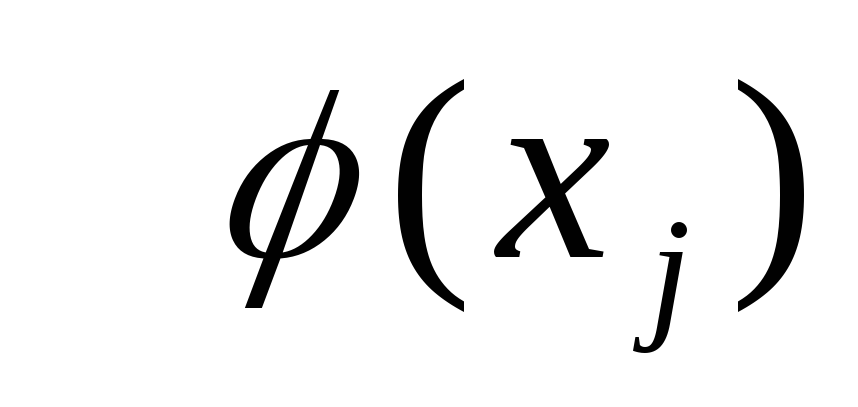в виде:

=.

Теперь, для того, чтобы принимало одно и только одно значение из множества (*), наложим на булевы переменные ограничение:

.

3. Произведем замену переменной :

.

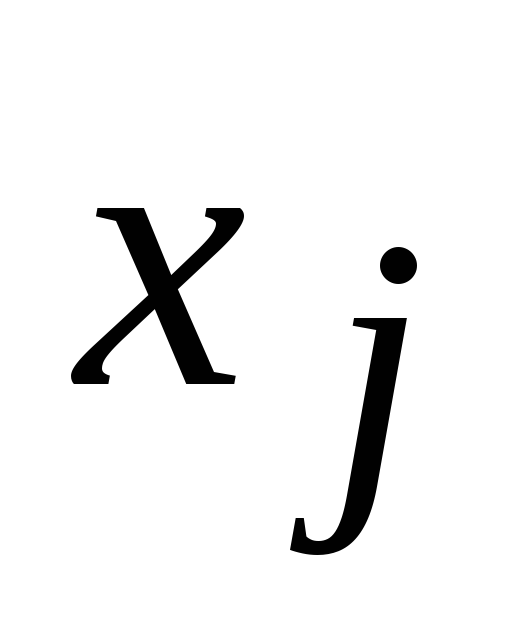Пример.  Дана нелинейная задача:

,

,

, ,

.

Свести задачу к задаче линейного программирования с булевыми переменными.

• Вводим булевы переменные y₁, y₂, y₃, y₄ ; y_l {0,1}, l=.

• Представляем   x₁   в виде:.

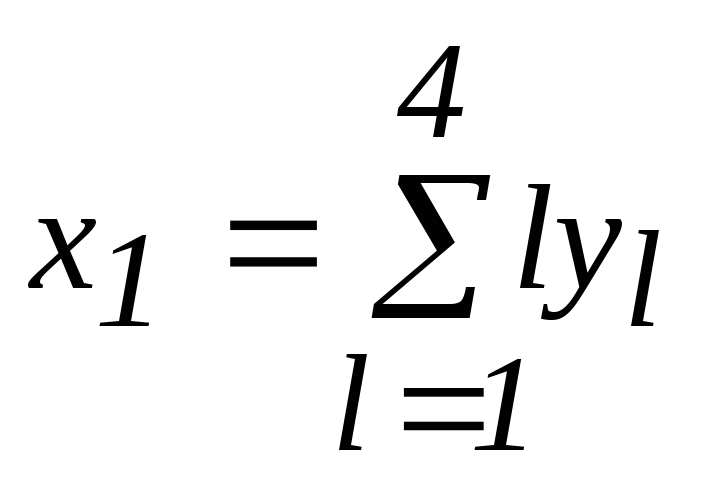• Потребуем, чтобы только одна булева переменная принимала единичное значение: .

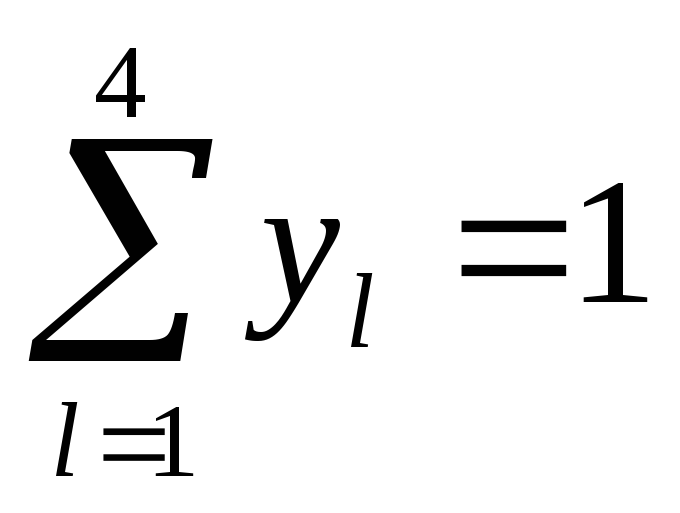• Представляем 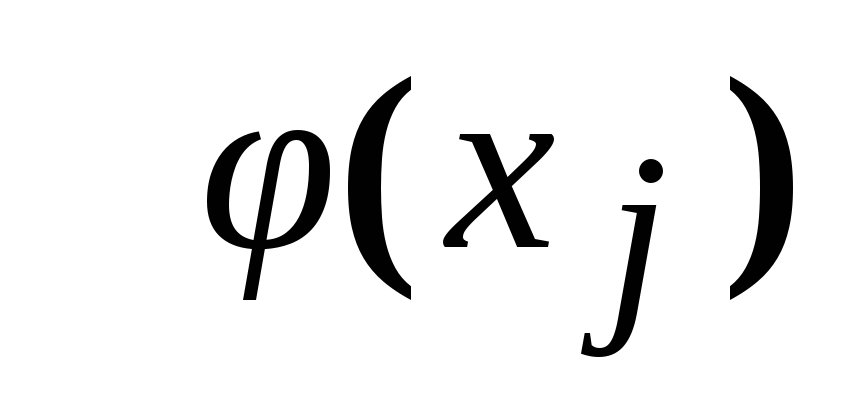в виде: =.

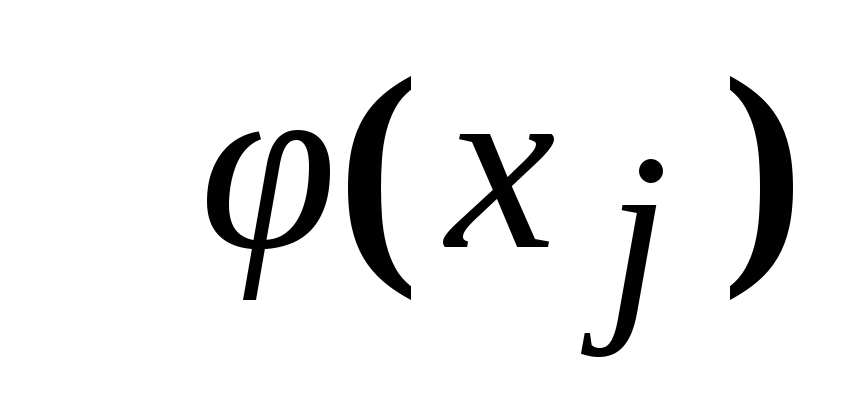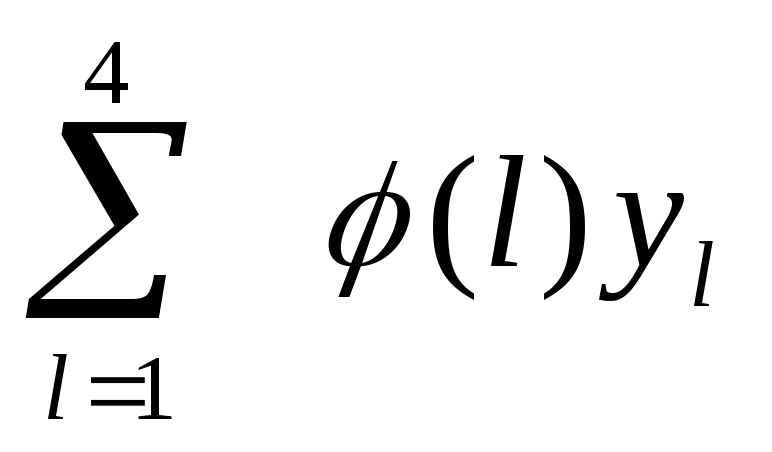• Окончательно:

,

,

,

,

y_l {0,1}, l=.

Пусть эта задача решена и ее решение представлено вектором:

.

По этому решению определяется оптимальное значение переменной   x₁   исходной задачи:

.