7

Лэнд и Дойг-штрафы.doc

Штрафы и их использование в методе Лэнд и Дойг Выбор переменной для ветвления в методе Лэнд и Дойг

Допустим, решена некоторая задача из списка задач и получено нецелочисленное решение этой задачи.

Оптимальная симплекс-таблица имеет вид:

Баз.	Cбаз	А0		ср		сj
				Ар		Aj
Ар	ср	xp0		1		xpj
		Z0		0		j0

Пусть x_p0 - значение некоторой базисной переменной x_p в оптимальном решении, не удовлетворяющее требованию целочисленности. Для определенности примем, что p{1,2,...,m}; а x_j , где j {m+1,m+2,...,n}  -  небазисные переменные.

В   p-той  строке последней симплекс-таблицы записано следующее уравнение:

x_p0= x_p+

или

x_p= x_p0  - (*)

Что означает ветвление по переменной x_p ?

Это означает, что необходимо сформировать две новые задачи, в систему ограничений одной из которых должно войти ограничение     x_p   [x_p0 ] + 1.

В систему ограничений другой задачи должно войти ограничение x_p   [x_p0 ] .

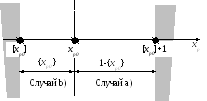
Случай a) :    Переменная x_p  должна принять значение, не меньшее, чем    [x_p0 ] + 1. Следовательно, эта переменная должна быть увеличена, по крайней мере, на величину:

1 - { x_p0}.

Как "поведут себя" свободные переменные?

x_p= x_p0  -

По крайней мере, одна из этих переменных (пусть это будет x_j), для которой x_pj<0, должна увеличиться на некоторую величину , которую можно найти из уравнения (*):

x_p+(1 - { x_p0})= x_p0  - x_pj(0 + ).

Здесь "0" - старое значение x_j ; "" - новое значение.

Ввиду того, что  x_p= x_p0  ,  имеет место:

1 - { x_p0}=   - x_pj . 

Отсюда определяется :

=.

Известно, что оценки свободных переменных - это взятые с обратным знаком коэффициенты, с которыми свободные переменные входят в целевую функцию, если базисные переменные выразить через свободные. То есть, справедливо следующее выражение:

Z = Z₀   - .

Пусть теперь переменная   x_j   увеличивается на величину =. Пусть, при этом, остальные свободные переменные не изменяют своих значений - остаются нулевыми. Следовательно, целевая функция должна уменьшиться на величину _j (помним, что x_pj < 0; кр. того ).

Теперь можно сделать вывод о том, что минимальная величина, на которую должно уменьшиться (ухудшиться) значение целевой функции в результате наложения ограничения x_p  [x_p0 ] + 1, определяется следующим образом:

.

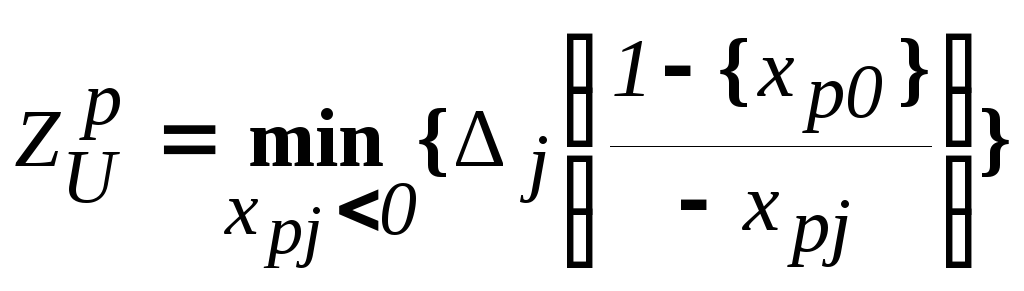Эту величину принято называть "ШТРАФОМ СВЕРХУ".

Следует подчеркнуть важное обстоятельство: для определения этого штрафа задачу можно не решать.

Всегда ли можно вычислить штраф сверху? Нет, не всегда. Действительно, может оказаться, что p-тая строка симплекс-таблицы не имеет ни одной отрицательной координаты x_pj < 0.

Вернемся к выражению   x_p= x_p0  -. Ограничение x_p  [x_p0 ] + 1 эквивалентно следующему ограничению:

x_p0  -  [x_p0 ] + 1. Отсюда следует:

  -1+ x_p0  - [x_p0 ] . Но   x_p0  - [x_p0 ] = { x_p0}, то есть:

  -1+ { x_p0}.

Для того, чтобы работать по симплекс-методу, это ограничение нужно привести к виду уравнения путем введения дополнительной переменной yp  0. Соответствующая строка симплекс-таблицы будет иметь вид:

-1+ { x_p0} =  + y_p .

Левая часть этого уравнения - отрицательное число. Оценки остались неотрицательными. То есть, теперь в симплекс-таблице записан псевдоплан: нужно работать по двойственному симплекс-методу. В столбце A0 есть единственный отрицательный элемент (-1+ { xp0} ), но в соответствующей этому элементу строке нет ни одной отрицательной координаты.

Это ‑ тот случай, когда в двойственном симплекс-методе срабатывает признак недопустимости задачи!

Таким образом, если штраф сверху не удается найти, соответствующую задачу можно не решать - она недопустима.

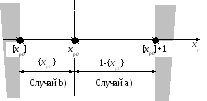
Случай   b) :    Переменная x_p  должна принять значение, не большее, чем    [x_p0 ] . Следовательно, эта переменная должна быть уменьшена, по крайней мере, на величину  { x_p0}.

Как "поведут себя" свободные переменные?

x_p= x_p0  -

Эти переменные могут только увеличиваться. По крайней мере, одна из этих переменных (пусть это будет x_j ) , для которой   x_pj > 0 ,  должна увеличиться на некоторую величину . Эту величину можно найти из уравнения (*):

x_p - { x_p0}= x_p0  - x_pj(0 + ).

Здесь "0" - старое значение x_j ; "" - новое значение.

Ввиду того, что  x_p= x_p0  ,  имеет место:

 - { x_p0}=   - x_pj . 

Отсюда определяется :

=.

Как было показано ранее:

Z = Z₀   - .

Пусть переменная   x_j   увеличивается на величину   =. Пусть, при этом, остальные свободные переменные не изменяют своих значений - остаются нулевыми. Следовательно, целевая функция должна уменьшиться на величину _j (помним, что x_pj > 0).

Теперь можно сделать вывод о том, что минимальная величина, на которую должно уменьшиться (ухудшиться) значение целевой функции в результате наложения ограничения x_p   [x_p0 ]  определяется следующим образом:

.

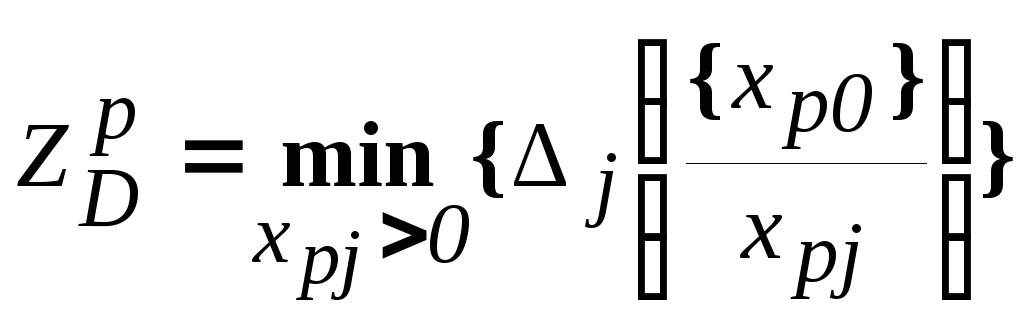Эту величину принято называть "ШТРАФОМ СНИЗУ".

Здесь, как и в предыдущем случае, для определения штрафа снизу задачу можно не решать.

Всегда ли можно вычислить штраф снизу? Нет, не всегда. Действительно, может оказаться, что p-тая строка симплекс-таблицы не имеет ни одной положительной координаты x_pj > 0.

Вернемся к выражению   x_p= x_p0  -. Ограничение x_p   [x_p0 ]  эквивалентно следующему ограничению:

x_p0  - [x_p0 ]. Отсюда следует: x_p0  - [x_p0 ] . Но   x_p0  - [x_p0 ] = { x_p0}, то есть:

 { x_p0}  .

Для того, чтобы работать по симплекс-методу, это ограничение нужно привести к виду уравнения путем введения дополнительной переменной y_p  0. Соответствующая строка симплекс-таблицы будет иметь вид:

- { x_p0} = - + y_p .

Левая часть этого уравнения - отрицательное число. Оценки остались неотрицательными. То есть, теперь в симплекс-таблице записан псевдоплан: нужно работать по двойственному симплекс-методу. В столбце A₀ есть единственный отрицательный элемент (- { x_p0} ), но в соответствующей этому элементу строке нет ни одной отрицательной координаты (т. к. все x_pj  0).

В двойственном симплекс-методе срабатывает признак недопустимости задачи!

Таким образом, если штраф снизу не удается найти, соответствующую задачу можно не решать - она недопустима.