7

Дробно-лин.doc Дробно-лин.doc

Дробно-линейное программирование

Задача о максимальной производительности

Для выполнения n различных работ могут быть использованы рабочие m квалификационных групп.

При выполнении i-той группой рабочихj-той работы выработка в единицу времени составляетc_ijединиц (i=1m;j=1n).

Общий фонд времени, в течение которого i-я группа рабочих может быть занята выполнением работ, не превышаетb_i единиц времени, аj-я работа должна быть выполнена в объеме не менееa_jединиц.

Необходимо составить такой план выполнения работ, который обеспечивает максимальную производительность.

Производительность=

Построение модели.

x_ij- время, затрачиваемоеi-той группой рабочих для выполненияj-той работы (i=1m; j=1n).

Тогда при плане { x_ij} общий объем работ (Z₁) составит:

Z₁=.

Общие затраты времени (Z₂) на выполнение этого объема работ определяются следующим образом:

Z₂=.

При плане { x_ij} общая производительность всех работ составит:

.

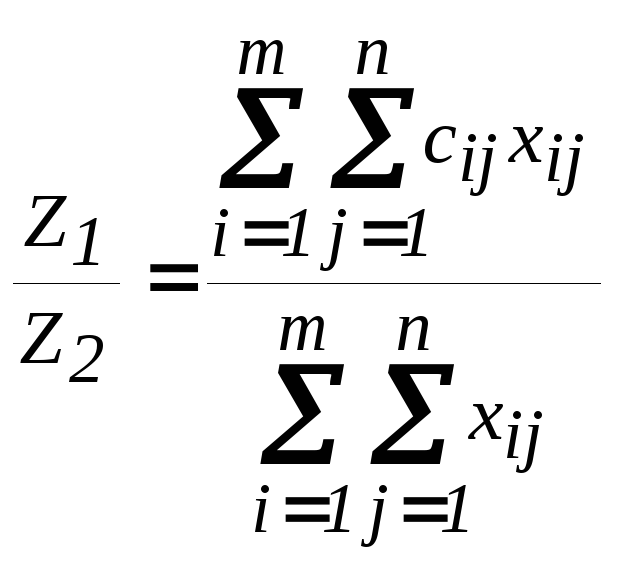Теперь об ограничениях.

j-я работа должна быть выполнена в объеме не менееa_jединиц. Следовательно, должно иметь место:

.

i-я группа рабочих может быть занята выполнением работ не болееb_i единиц времени:

Последнее, естественное, ограничение - это требование не отрицательности переменных: x_ij  0, (i=1m;j=1n).

Окончательно модель приобретает вид:

,

,

,

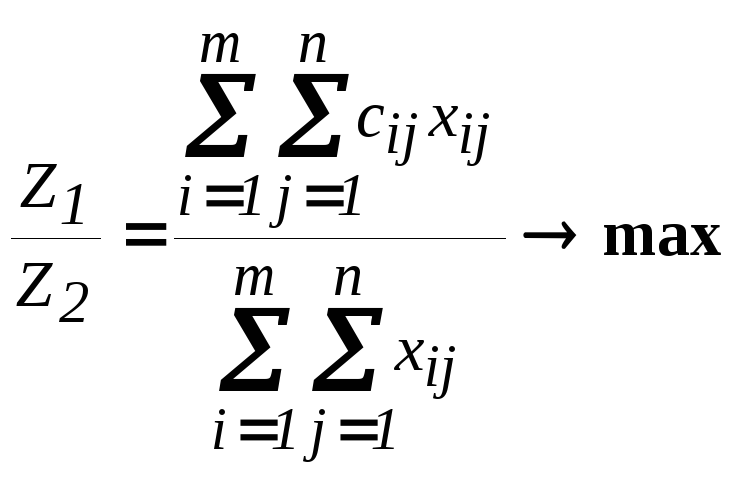x_ij  0, (i=1m;j=1n).

В практике планирования с использованием математических моделей оптимизационных задач подобные нелинейные задачи встречаются довольно часто. Они составляют целый класс задач математического программирования - класс задач "дробно-линейного" (ДЛП) или "гиперболического" программирования. В общей постановке задача ДЛП имеет вид:

Z=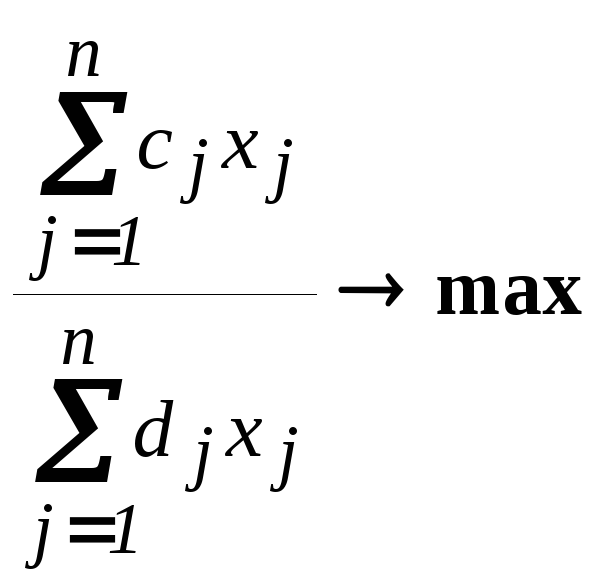, (1)

, (2)

x_j  0, (j=1n). (3)

При этом предполагается, что и, кроме того,в области неотрицательных решений системы уравнений (2). Заметим, что условиев этой области не нарушает общности задачи, так как в противном случае знак минус всегда можно отнести к числителю.

Что характерно для этой задачи? Как и в случае общей задачи ЛП, своего максимального значения ЦФ (1) достигает в одной из вершин выпуклого многогранника, определяемого ограничениями (2) и (3) (естественно, при условии, что задача имеет решение). Если же ЦФ принимает максимальное значение более, чем в одной вершине, то она достигает это значение в любой точке, являющейся выпуклой линейной комбинацией данных вершин.

Эти свойства хорошо иллюстрируются путем геометрической интерпретации задачи ДЛП.

Геометрическая интерпретация задачи длп

Рассмотрим случай двух переменных:

,

(i=1,2,...,m),

x₁, x₂0.

Будем считать, что в области допустимых решений (D) имеет место:d₁x₁+ d₂x₂ 0.

Для того чтобы найти решение задачи, сначала построим многогранник решений, определенный ограничениями задачи.

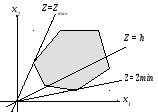
Положим значение ЦФ равным некоторому числу h.То есть ЦФ будет принимать одно и то же значение во всех точках прямойили :

(с₁-d₁h)x₁+(с₂-d₂h)x₂=0. (*)

Очевидно, что эта прямая проходит через начало координат. Для того чтобы найти допустимые решения, на которых ЦФ принимает значение h, прямая должна иметь общие точки с многоугольником.

Начнем увеличивать параметр h. Увеличение этого параметра приведет к вращению прямой (*) вокруг начала координат либо по либо против часовой стрелки, в зависимости от сочетания параметровc_j , d_j(j=1,2).

Из геометрических соображений ясно, что, если допустимое множество ограничено, при некотором значении h=h^*прямая (*) станет опорной к допустимому множеству. При этом в точке (точках) касания будет достигнуто искомое оптимальное решение.

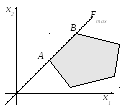
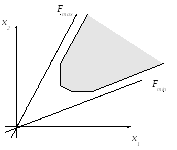
На этом рисунке представлен случай, когда максимум ЦФ достигается в любой точке отрезка [A,B].

Представляет интерес случай, когда допустимое множество не ограничено. Здесь возможны следующие ситуации.

1. Допустимое множество не ограничено, однако существуют вершины, в которых ЦФ принимает соответственно максимальное и минимальное значение:

2. Допустимое множество не ограничено, и один из экстремумов не достигается. Например, минимум достигается в одной из вершин, а максимум не достигается вообще:

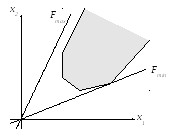
Это - случай, т.н. "асимптотического максимума".¹

В принципе, возможна ситуация, когда имеет место и асимптотический максимум, и асимптотический минимум: