19

Переходная и импульсная функции.

Введем две функции, имеющие большое значение в теории цепей: единичную ступенчатую и единичную импульсную. Вводить их будем без математического основания, которое может быть произведено с помощью теории обобщенных функций.

Обобщенные функции.

Обобщенными функциями называют функции времени f(t), которые терпят разрыв, например, при t=0. Значение функции при t<0 обозначим f_–(t), при t>0 – f₊(t). Например, см. рис. 5.13.

f₊(t)

f_–(t)

t

Рис. 5.13

Введение ступенчатой импульсной функции является следствием введения идеальных источников и элементов.

Единичная ступенчатая функция (функция Хэвисайда) представляет собой с точки зрения теории электрических цепей единичное постоянное напряжение или ток, действующее на входе цепи с момента t = 0₊ так, что

1(t)=0 , при t<0 ;

1(t)=1 , при t>0 .

1(t)

1

t

Рис. 5.14

Функция h(t), представляющая собой реакцию цепи на единичный скачек, численно равная искомому току (или напряжению), называется переходной функцией или переходной характеристикой.

Примеры:

Для RL цепи, представленной на рис. 5.15

i R L

U

Рис. 5.15

Переходная функция тока:

.

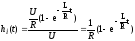А для RC цепи на рис. 5.16:

i R С

U

Рис. 5.16

Переходная функция напряжения на емкостном элементе:

.

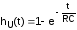Рассмотрим рис. 5.15.

1. До коммутации: i=0.

2. Независимые начальные условия: i(0_–)= i(0₊)=0.

3. Линейное дифференциальное уравнение после коммутации:

.

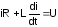4. Принужденная составляющая (t): .

5. Свободная составляющая:

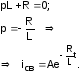
6. Общий вид: .

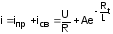7. Определение постоянных интегрирования:

8) Окончательно:

Рассмотрим рис. 5.16.

1. До коммутации: U=0.

2. Независимые начальные условия: U_c(0_–)= U_c (0₊)=0.

3. Линейное дифференциальное уравнение после коммутации:

.

4. Принужденная составляющая (t): U_c = U, так как i_R = 0.

5. Свободная составляющая:

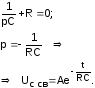
6. Общий вид: .

7. Определение постоянных интегрирования:

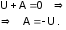
8) Окончательно: .

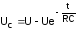Переходную функцию h(t) при любой схеме пассивного двухполюсника можно найти классическим методом (или операторным методом, или методом интеграла Фурье, о чем речь пойдет ниже).

Таким образом, в дальнейших расчетах будем считать функцию h(t) известной (при t<0 h(t)=0).

Пусть произвольный пассивный линейный двухполюсник подключается к источнику непрерывно изменяющегося с момента t=0 напряжения (рис. 5.17). Требуется найти ток (или напряжение) в любой ветви двухполюсника.

u(t)

u() u

u(0)

t –

t

Рис. 5.17

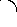
Решение:

Непрерывно изменяющееся u(t) заменим ступенчатой функцией с элементарными прямоугольными скачками u. Тогда процесс изменения напряжения можно представить как включение при t=0 постоянного напряжения u(0), а затем как включение элементарных постоянных напряжений u, смещенных относительно друг друга на интервалы , имеющих знак “+” для возрастающей и ”–“ для убывающей части кривой напряжения. Составляющая искомого тока в момент t от постоянного напряжения на входе u(0) равна u(0)h(t).

Составляющая искомого тока элементарного скачка напряжения u, включаемого в момент времени равна u^.h(t– ). Здесь аргументом переходной функции служит время (t – ), поскольку элементарный скачок u начинает действовать на время позднее замыкания ключа.

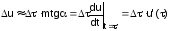, где

m – масштабный коэффициент (соответствие градуировки оси x градуировке оси y).

Поэтому:

.

Элементарные скачки напряжения включаются на интервале времени от t=0 до t , для которого определяется искомый ток. Поэтому, суммируя составляющие тока от всех скачков, переходя к пределу при 0 и учитывая составляющую тока от начального скачка напряжения u(0), получаем

.

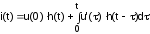Последняя формула для определения тока при непрерывном изменении приложенного напряжения называется формулой (интегралом) Дюамеля. Аналогично решается задача при подключении цепи к источнику тока.

С помощью теоремы свертки двух функций f₁(t) и f₂(t):

можно получить другие формы записи.

Усложним задачу. Пусть произвольный пассивный двухполюсник подключен к источнику напряжения, кривая изменения которого дана на рис. 5.18.

u(t)

u₁(t)

u(0)

t

t₁ t₂

u₂(t)

Рис. 5.18

Решение:

Для вычисления тока определим переходную функцию h(t):

0< t< t₁: .

Для учета скачка напряжения в точке t = t₁ будем считать, что в этот момент к двухполюснику прикладывается отрицательное постоянное напряжение U = u₂(t₁) – u₁(t₁). Кроме того, учтем составляющие тока от начального скачка напряжения u₁(0) и от элементарных скачков напряжения, определяемого кривой u₁(t) и действующего от t=0 до t=t₁. В результате получим:

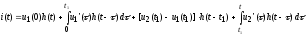Для промежутка t₂ < t < включается постоянное напряжение u = – u₂(t₂).

В итоге:

При подключении активного двухполюсного элемента к источнику напряжения, расчет проводится по принципу наложения.

Расчет с помощью интеграла Дюамеля проводят в 4 этапа:

1. Определение переходной функции h(t) для исследуемой цепи.

2. Определение h(t – ). С этой целью в функции h(t) заменяют t на (t – ).

3. Определение u’(). Для этого находят производную от заданного напряжения u(t) по времени t, и в полученном выражении заменяют t на .

4. Подстановка найденных на этапах 1, 2, 3 функций в формулу интеграла Дюамеля, интегрирование по переменной и подстановка пределов.

Таким образом, если определена характеристика h(t), то при помощи интеграла Дюамеля можно определить реакцию системы при любой форме внешних воздействий.

Пример:

r₁ i₁

u(t) r₂ L i_L

i₂

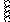
u(t)

100 В

t

1.25 2.5

мс мс 100 В

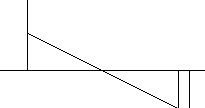
Рис. 5.19

Рис. 5.20

Определить переходную функцию h(t) для цепи, представленной на рис. 5.19 . С учетом входного воздецствия, представленного на рис. 4.20 определить i_L (t). r₁ = 2 Ом ; r₂ = 5 Ом ; L = 4 мГн.