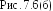Лекции по ТОЭ10 / PART7-1

14

7. СПЕКТРЫ ПЕРИОДИЧЕСКИХ И АПЕРИОДИЧЕСКИХ ФУНКЦИЙ, СПЕКТРАЛЬНЫЙ АНАЛИЗ.

ИЗОБРАЖЕНИЕ НЕСИНУСОИДАЛЬНЫХ ТОКОВ И НАПРЯЖЕНИЙ С ПОМОЩЬЮ РЯДОВ ФУРЬЕ

Из курса математики известно, что любую периодическую функцию f(x), удовлетворяющую условиям Дирихле можно разложить в ряд Фурье.

Ряд Фурье можно записать двояко:

1 форма записи:

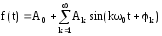(1)

2 форма записи:

(2)

А₀ – постоянная составляющая ряда

А_k – амплитуда к-й гармоники

j_к - начальная фаза к-й гармоники

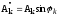
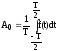
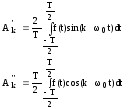
иначе 2-я формула выглядит так:

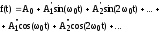
Гармоники, для которых к – нечетное число – называют нечетными.

Ряд, представленный формулами (1) или (2) называют рядом Фурье, а совокупность коэффициентов А₀; А^’_к; А^’’_k – гармоническим спектром периодического сигнала.

Такое разложение по ряду причин играет большую роль. Во-первых, гармоническое колебание является единственной функцией времени, сохраняющей свою форму при прохождении через любую линейную цепь (с постоянными параметрами). Изменяется лишь амплитуда и фаза колебаний. Во-вторых, разложение сложного сигнала на синусные и косинусные составляющие позволяет использовать символический метод, разработанный для анализа передачи гармонических колебаний через линейные цепи. По этим, а также и некоторым другим принципам гармонический анализ получил широкое распространение во всех отраслях современной науки и техники.

При 1-й форме записи ряда Фурье расчет коэффициентов А_к и j_к не упрощается, но физический смысл их более доступен. Периодический сигнал разлагается на постоянную составляющую А₀ и состовляющие вида А_ksin(kw₀ t+j_к), называемые гармониками. Причем А_к имеет смысл амплитуды гармоники, а j_к – ее начальной фазы.

Зависимость А от частоты называют амплитудным спектром периодического сигнала, аналогичную зависимость для j_к фазовым спектром.

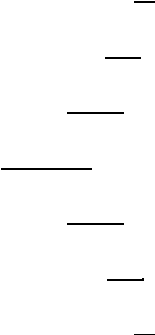
Наглядное представление о “ширине” спектра дает графическое изображение спектра амплитуд. Например,

(см. рис. 7.1)

Для исчерпывающей характеристики спектра подобные постороения должны дополнены заданием начальных фаз отдельных гармоник, например, рис. 7.2

Спектр периодической функции называется линейным или дискретным, т.к. состоит из отдельных линий, соответствующих отдельным частотам: 0, w₁,; w=2w; w=3w и т.д.

Сложные периодические системы можно изображать и графически на временной диаграмме. Однако это сложно и неудобно. Поэтому предыдущий способ изображения дискретных спектров в виде отрезков линий более предпочтителен.

НЕКОТОРЫЕ СВОЙСТВА ПЕРИОДИЧЕСКИХ КРИВЫХ, ОБЛАДАЮЩИХ СИММЕТРИЕЙ

А. Кривая, которая при смещении по оси Х на Т/2 будет симметрична относительно оси абсцисс (может быть представлена следующей аналитической зависимостью).

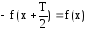
Пример такой кривой можно увидеть на рис. 7.3

При разложении подобных кривых в ряд Фурье отсутствует постоянная составляющая и четные гармоники. т.е. коэффициенты А₀ = А^’₂ = А^’’₂ = … =0.

Поэтому функции подобного типа раскладываются в ряд

f(x)=A^’₁ sinx + A^’’₁ cosx + A^’₃ sin3x + …

Б. Кривая,удовлетворяющая условию: f(-x)=f(x) обладает симметрией относительно оси ординат. Пример можно увидеть на рис. 7.4.

При разложении в ряд Фурье будут отсутствовать синусные (А^’₁ =А^’₂ =А^’₃ =0) и присутствовать лишь косинусные составляющие с постоянной состовляющей. Таким образом

f(x)=A₀ +A^’’₁ cosx + A^’’₂ cos2x + A^’’₃ cos3x + …+A^’’_k coskx.

В. Кривые, симметричные относительно начала координат:

-f(-x)=f(x)

Разложение их в ряд Фурье имеет вид:

f(x)=A^’₁ sinx + A^’₂ sin2x + A^’₃ sin3x + …+A^’_k sinkx .

Кривые правильной формы (трапецеидальные, треугольные, прямоугольные) можно раскладывать в ряд Фурье пользуясь специальными таблицами .

Периодические кривые произвольной (геометрически неправильной) формы раскладываются в ряд Фурье графически (графо-аналитические). Метод основан на замене конечного интеграла суммой конечного числа слагаемых. С этой целью период функции f(x), равной Т=2p разбивают на n равных частей и интегралы заменяют суммами.

,

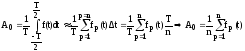где

р – текущий индекс, принимающий значения от 1 до n,

f_p(t) – значение функции f(t) при t=(p-0.5) Dt , т.е. в середине

р-го интервала.

Амплитуда синусной составляющей к=й гармоники ряда:

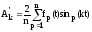
где sin_p kt – значение функци sinkt в середине р-го интервала.

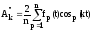
При расчетах по этим формулам достаточно обычно разделить период на n=24 или 18 частей, а в некоторых случаях и на меньшее число частей.

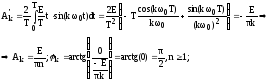
В качестве примера расчитаем и постоим график гармонического спектра периодического сигнала, изображенного на рис. 7.5 и запишем для него ряд Фурье:

;

–

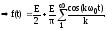
РАСЧЕТ ТОКОВ И НАПРЯЖЕНИЙ ПРИ НЕСИНУСОИДАЛЬНЫХ(ПЕРИОДИЧНЫХ) ИСТОЧНИКАХ ПИТАНИЯ

До проведения расчета вынуждающие силы (ток и ЭДС) должны быть представлены рядами Фурье. Согласно принципу наложения, мгновенное значение тока любой ветви схемы равно сумме мгновенных значений токов отдельных гармоник. Расчет производят для каждой из гармоник в отдельности с помощью уже известных приемов.

При расчете каждую гармонику выражают комплексным числом. Суммирование одноименных гармоник производят путем сложения комплексных чисел или векторов на комплексной плоскости.

РЯД ФУРЬЕ В КОМПЛЕКСНОЙ ФОРМЕ ЗАПИСИ

Перейти к комплексной форме записи можно используя соотношение:

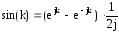, т.к.

Используя 1 форму записи ряда Фурье:

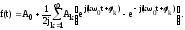
Если ввести 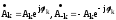, то

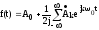- комплексная форма записи ряда Фурье.

Интервал К может принимать все целые числовые значения от

– ¥ до + ¥. , но неравные 0 ,т.к. постоянная составляющая выделена в виде отдельного слагаемого.

Пример: представить функцию

f(t)=2 + 3sin(w₀t + 30^o) + 2 sin (2 w₀ t – 45^o)

в комплексной форме записи.

Решение:

; ; ; ; ;

.

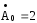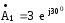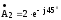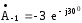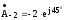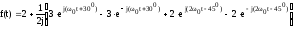Продолжая преобразовывать ряд Фурье в комплексной форме записи составим выражение для . По определению

В ряде учебных пособий предлагается следующая форма записи ряда Фурье в комплексной форме:

, при к=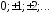

где

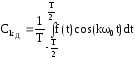- Действительная часть

- Мнимая часть

В этой форме записи ряда Фурье совокупность величин С_к называют комплексным спектром Фурье периодического сигнала. При графическом изображении необходимо построить 2 функции С_k =f₁ (kw₀) – зависимость модуля от частоты и j_к =f₂ (nw₀) - зависимость аргументов коэффициентов комплексного ряда от частоты.

Рассмотрим и постоим комплексный спектр периодического сигнала рассмотренный в предыдущем примере (см. рис. 7.5)

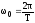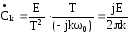Т.к. , то при

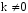
Тогда коэффициент С_к легко представить в векторной форме, учитывая что

;

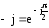
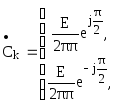
при k>0

при k<0