6. Операторный метод анализа электрических цепей.
Операторный метод основан на использовании понятия об изображении функции времени. В операторном методе каждой функции времени соответствует функция новой переменной, обозначаемой буквой p, и наоборот – функции переменной p отвечает определенная функция времени.
Переход от функции времени к функции p осуществляется с помощью прямого преобразования Лапласа. В отличие от классического метода расчета, где решаются системы дифференциальных уравнений, операторный метод сводит операцию дифференцирования к умножению, а операцию интегрирования – к делению.
Под p условимся принимать комплексное число p = + j (можно рассматривать как комплексную частоту). Функцию времени (ток, напряжение) обозначают f(t) и называют оригиналом. Ей соответствует функция F(p) – изображение. Соответствие F(p) = f(t) устанавливается с помощью преобразований:
прямое преобразование Лапласа:
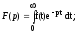 (1)
(1)
обратное преобразование Римана-Мелина:
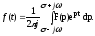 (2)
(2)
Наряду с преобразованием Лапласа применяется преобразование Карсон-Хэвисайда:
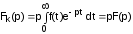 .
.
Найдем изображение некоторых простейших функций:
Изображение постоянной. f(t)=A

Изображение показательной функции
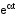 .
.
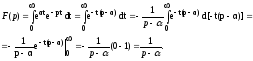
Интеграл сходится только в случае, если действительная часть оператора p > .
Из последней формулы следует, что
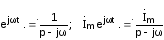 .
.
Изображение первой производной
 .
.
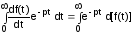 .
.
Произведем интегрирование по частям.
e-pt = u и d[f(t)] = dv ;
 ;
;
Исходя
из этого:
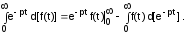
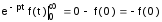 ;
; .
.
Таким
образом, ![]()
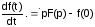 .
.
На индуктивности: .
Изображение интеграла

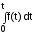 .
.
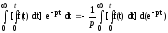 .
.
Проинтегрируем по частям:

Изображение напряжения на конденсаторе.
Напряжение на конденсаторе uc часто записывают в виде:
 ,
,
где не указаны пределы интегрирования по времени. Более полной является следующая запись:
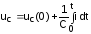 ,
,
где учтено, что к моменту времени t напряжение на конденсаторе определяется не только током, протекающим через C в интервале времени от 0 до t, но и тем напряжением uc(0), которое было на нем при t=0.
Поэтому: 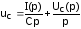 .
.
Простейшие операторные соотношения содержатся в справочном материале многих учебных пособий в виде готовых таблиц.
Отметим основные свойства преобразования Лапласа:
Соответствие между оригиналом и изображением взаимно однозначно: каждой функции f(t) соответствует F(p) и наоборот.
При умножении оригинала f(t) на постоянную величину , умножается и изображение:
f(t) . = F(p) .
Изображение суммы функций равно сумме изображений этих функций.
Теоремы операционного исчисления (с учетом f(t) = F(p).
Теорема подобия:
Умножение аргумента оригинала на положительное число a (a>0) приводит к делению аргумента изображения и самого изображения на то же число a:
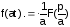 .
.
Теорема запаздывания:
Запаздывание
функции на время t1
соответствует умножению ее изображения
на
 :
:
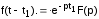 .
.
Теорема смещения (затухания):
Умножение функции f(t) на экспоненциальный множитель e–t ведет за собой «смещение» в области аргумента изображения с p на p+:
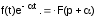 .
.
Пример 1 :
Найти
оригинал
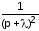 , если известно, что
, если известно, что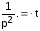 .
.
Решение:
По теореме смещения:
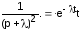 .
.
Теорема дифференцирования изображений:
Дифференцирование изображения F(p) по p соответствует домножению оригинала на (–t):
F’(p) = – t f(t) .
Остановимся более подробно на переходе от изображения к оригиналу. Использование интеграла Римана-Мелина требует применения методов теории вычетов, поэтому на практике наибольший интерес с точки зрения экономии времени представляет возможность определения оригиналов по известным изображениям с помощью таблиц и теорем.
Пример 2 : Найти оригинал изображения:
 .
.
Решение:
F(p – ) . = et f(t) – теорема смещения.
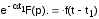 –теорема
запаздывания.
–теорема
запаздывания.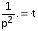 (см.
предыдущий пример).
(см.
предыдущий пример).(1) и (3)
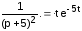 .
.(4) и (2)
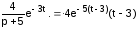 .
.
Пример 3 : Найти изображение функции
f(t) = 3t sin 0t , при t>0,
с
учетом того, что
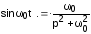 .
.
Решение:
Согласно теореме дифференцирования изображения:
F’(p) . = – t f(t) .
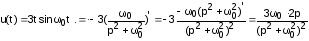 .
.
Если же изображение искомой функции получилось сложным и его не оказалось в самых подробных таблицах, то следует воспользоваться аналитическими методами. В частности – использовать теорему разложения. Эта теорема позволяет по известному изображению функции в виде рациональной дроби:

найти соответствующий ей оригинал, где
B(p) = bmpm + bm-1pm-1 + … + b1p + b0 = bm (p–p1)(p–p2)…(p–pm) .
p1, p2, … , pm – корни уравнения B(p)=0.
Теорема разложения аналитически представляется формулой:
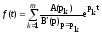 .
.
Доказательство:
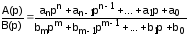 .
.
Из
курса математики известно, что если
n<m,
ak
и
bk
– вещественные
числа, а корни p1,
p2,
… , pm
уравнения
B(p)=0
различные,
то дробь
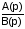 может быть представлена в виде суммы
простых дробей:
может быть представлена в виде суммы
простых дробей:
 .
.
Для определения коэффициента A1 умножим обе части уравнения на (p–p1):
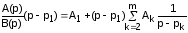 .
.
Рассмотрим это выражение при pp1. Правая часть дает A1, левая представляет собой неопределенность, так как множитель (p–p1) дает ноль, и знаменатель B(p) при p=p1 тоже обращается в ноль.
Раскроем неопределенность по правилу Лопиталя. С этой целью производную от числителя разделим на производную от знаменателя, и найдем предел дроби.
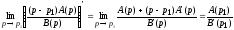 ,
где
,
где
B’(p) – производная от B(p) по p,
B’(p1) – значение B’(p) при p=p1,
A(p1) – значение A(p) при p=p1.
Следовательно, при pp1 получаем уравнение:
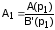 .
.
Аналогично:
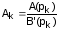 .
.
Таким образом,
 .
.
Пусть изображение какой-либо функции времени, например тока, представлено в виде дроби:
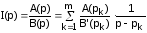 .
.
Перейдем
от изображения к оригиналу. Оригиналом
левой части является i(t).
Оригинал правой части равен сумме
оригиналов ее слагаемых. Так как множители
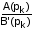 – есть постоянные числа, а функциямиp
являются множители
– есть постоянные числа, а функциямиp
являются множители
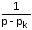 ,
которым соответствуют функции времени
вида
,
которым соответствуют функции времени
вида .
Поэтому:
.
Поэтому:
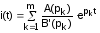 .
.
Последовательность вычислений по формуле такова:
Приравниваем B(p) к нулю и определяем корни p1, p2, … ,pn.
Вычисляем производную B’(p) и подставляем в нее корни p1, p2, … ,pn (поочередно).
Подставляем в числитель корни p1, p2, … ,pn. Определяем его значения – A(pk).
Вычисляя отдельные слагаемые и суммируя их, определяем оригинал f(t).
Пример:
Пусть
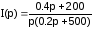 . Получитьf(t).
. Получитьf(t).
Решение:
I способ: преобразовать I(p) так, чтобы получить табличные изображения:
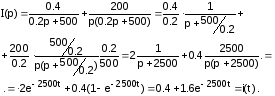
II способ: Используем теорему разложения:
A(p) = 0.4p + 200 ;
B(p) = p(0.2p + 500) .
Вычислим корни B(p)=0:
p(0.2p + 500) = 0 p1 = -2500 c-1
p2 = 0 .
A(p1) = -800 , A(p2) = 200 ;
B’(p) = 0.4p + 500 ;
B’(p1) = -500 , B’(p2) = 500 .
Подставляя найденные значения в формулу разложения, получим:
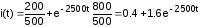 .
.
Замечания к формуле разложения:
Формула разложения применима при любых начальных условиях и при любых практически встречающихся формах напряжения источника эдс или тока, воздействующего на схему.
Если уравнение B(p)=0 имеет комплексно-сопряженные корни, то слагаемые в формуле разложения оказываются также комплексно-сопряженными и в сумме дают действительное слагаемое.
Пример:
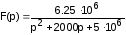 .
f(t) – ?
.
f(t) – ?
Решение:
p1,2 = -1000 j2000 c-1.
B’(p) = 2p + 2000 B’(p1) = j4000
B’(p2) = -j4000 .