Резонанс в сложных цепях.
Условия резонанса b=0 или x=0 для разветвленной цепи с несколькими катушками индуктивности и конденсаторами дают для частоты w уравнения, которые могут иметь несколько действительных корней. Иначе у подобной цепи может быть несколько резонансных частот.
Рассмотрим, например, цепь на рис. 2.32, потерями в которой можно пренебречь. Входное сопротивление цепи реактивно.
L3
L1 C2
Рис. 2.32
где
x – мнимая часть сопротивления
Резонанс
наступает при b=0
(реактивная составляющая проводимости)
или x=0
(реактивная составляющая сопротивления).
Причем, если x=0, то b и наоборот, если b=0, то x.
Резонансными будут частоты, обращающие x в ноль или бесконечность. В рассматриваемом случае x= при w2L1C2 – 1=0
или
.
При этой частоте наступает резонанс токов в параллельных ветвях с L1 и C2. Полагая x=0, получаем
При этой частоте имеет место резонанс напряжений в последовательном колебательном контуре с индуктивностью L3 и емкостью, эквивалентной двум параллельным ветвям.
b1x x’=1/b’
x3=wL3
x
b1=1/wL1
w wн w
b’=b1+b2
b2= –wC2
Рис.2.33
На рисунке 2.33 приведены частотные характеристики проводимости и сопротивлений для рассматриваемой цепи. Кривые b1=1 / wL1 и b2 = –wC2 представляют характеристики проводимостей ветвей 1 и 2. Суммируя ординаты этих кривых получаем характеристику, эквивалентную проводимости b’ двух параллельных ветвей 1 и 2. Кривая x’ = 1 / b’ представляет эквивалентное сопротивление параллельных ветвей. Суммируя ординаты кривых x1 и x2, построим характеристику входного сопротивления цепи x. Эта характеристика имеет две особые точки w=w (резонанс токов), w=wн (резонанс напряжений).
Определить последовательность чередования резонансов токов и напряжений в сложном колебательнеом контуре можно по следующему правилу:
В электрической цепи, составленной из n реактивных элементов возникает не более (n–1) резонансов. Резонансы токов и напряжений чередуются между собой. Если в цепи есть путь для прохождения постоянного тока, то есть при w=0, входное сопротивление минимально, то первым наступит резонанс токов, если нет (при w=0 zвх=), то первым наступит резонанс напряжений.
Сложные колебательные контуры могут использоваться для подавления специфических помех на фиксированных частотах. В сложном колебательном контуре, настроенном на частоту полезного сигнала w0 , резонансная частота w или w2 может быть выбрана равной частоте помехи (см. рис.2.34). При этом за счет малого коэффициента передачи на частоте резонанса напряжений достигается особенно сильное подавление помехи.
K
w0 w2 w
а)
K
w1 w0 w
б)
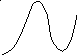
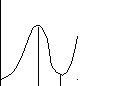
Рис.2.34 Частотные характеристики сложных контуров.
Например, в радиопередатчике за счет нелинейных процессов могут возникнуть паразитные колебания на частотах высших гармоник полезного сигнала. В этом случае в передатчике можно применить сложный контур с частотной характеристикой, показанной на рис. 2 а), и выбрать, например, w2 = 2w0 или 3w0. Тогда будет обеспечено эффективное подавление соответствующей высшей гармоники.
В контуре с характеристикой как на рис.2.34 б можно выбрать w0 = 2w1 или 3w1. При этом наоборот, можно выделить колебания с повышенной частотой w0 и подавить помехи на пониженной частоте w1. Такой способ выделения колебаний повышенных частот может быть применен в умножителях частоты. В этих нелинейных устройствах при подведении задающих колебаний с частотой w1 возникают высшие гармоники, одна из которых и выделяется сложным контуром. Одновременно этот контур подавляет задающие колебания, которые для умножителя частот являются помехой.
Пример: Дана цепь, состоящая из четырех реактивных элементов (см.рис.2.35). Качественно построить характеристику сопротивления такой цепи.
С1
L1
L2
C2
Рис.2.35
Решение:
В данной цепи могут возникнуть 3 резонанса, причем первым наступает резонанс токов. Характеристика такой цепи приведена на рисунке 2.36.
Резонансные частоты обозначены точками: w1; w2; w3.