28

2. Анализ установившегося режима в цепях синусоидального тока. Гармонические функции.

Функция называется гармонической, если ее значение a(t) изменяется по синусоидальному или косинусоидальному закону.

a(t)=A_m cos(wt+) = A_m sIn(wt+’).

Наибольшее значение гармонической функции называют амплитудой A_m . Аргумент =wt+ – называют мгновенной фазой. Величина , равная значению мгновенной фазы при t=0 называется начальной фазой.

Скорость изменения фазы называется угловой скоростью.

Если значения функции повторяются через определенные промежутки времени, то такую функцию называют периодической. Наименьший промежуток T, через который наблюдается повторение значений функций, называется периодом.

Величина, обратная Т ( =1/ f ), называется частотой. В России и Западной Европе наибольшее распространение получили установки с частотой 50 Гц. В США – стандартной является частота 60 Гц.

Под средним значением периодической функции a(t) понимают ее среднее значение за пол периода.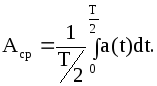

Широко применяется понятие действующего значения синусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным).

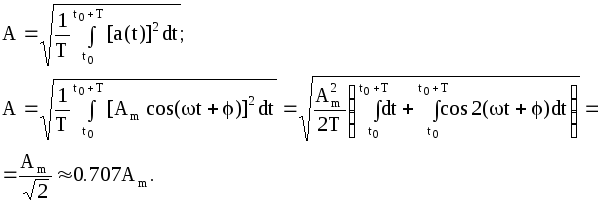
Изображение синусоидально изменяющихся величин на комплексной плоскости.

Комплексное число имеет действительную и мнимую части. Комплексное число может быть представлено в виде вектора на комплексной плоскости. По оси абсцисс комплексной плоскости откладывают действительную часть комплексного числа, а по оси ординат – мнимую (см. рис. 2.1).

Im

sin

e^j

cos Re

Рис. 2.1

Из курса математики известна формула Эйлера:

e^j = cos +j sin .

Комплексное число e^j изображают на комплексной плоскости вектором, численно равным 1 и составляющим угол с осью вещественных значений (осью +1). Угол отсчитываем против часовой стрелки от оси действительных значений. Модуль функции:

Проекция функции e^j на ось действительных значений равна cos , а на ось мнимых значений – sin .

Если вместо функции e^j взять функцию I_me^j , то

I_me^j = I_mcos + j I_msin .

Угол может быть любым. Пусть =wt+, то есть угол изменяется пропорционально времени. Тогда

I_me^j(wt+) = I_mcos(wt+) + j I_msin(wt+).

На комплексной плоскости принято изображать величины для момента времени wt=0. Хотя синусоидально изменяющийся ток i можно представить как проекцию вращающегося вектора I_m e^j(wt+) на ось действительных значений или j.

Если мы имеем два тока (I₁ и I₂), протекающих в одной ветви с одинаковой частотой, то их можно изобразить на одной комплексной плоскости и сложить по правилам векторной алгебры (см рис.2.2).

+j

Рис. 2.2

Обратить внимание, что если бы векторы , , стали бы вращаться вокруг начала координат с угловой скоростью w, то

взаимное расположение векторов по отношению друг к другу осталось бы без изменений и если бы вращались с разными угловыми скоростями, то их изображение на одной комплексной плоскости не имело бы смысла.

Таким образом, комплексная амплитуда гармонической функции времени a(t)=A_mcos(wt+) представляет собой комплексное число, модуль которого равен амплитуде A_m , а аргумент – ее начальной фазе . Геометрически комплексная амплитуда может быть представлена в виде неподвижного вектора, направленного под углом к вещественной оси, длина которого в определенном масштабе равна A_m.