3.1.1. Требования к исходной информации

Анализ временных рядов, отражающих развитие эко­номических процессов, начинается с оценки данных. Уровни ис­следуемого показателя обязательно должны быть сопоставимыми, однородными и устойчивыми, а их число должно быть достаточно велико.

Сопоставимость достигается в результате одинакового подхода к наблюдениям на разных этапах формирования динамического ряда. Уровни во временных рядах должны иметь одинаковые:

• единицы измерения;

• шаг наблюдений;

• интервал времени;

• методику расчета;

• элементы, относящиеся к неизменной совокупности.

Однородность данных означает отсутствие сильных изломов тенденций, а также аномальных (т.е. резко выделяющихся, нети­пичных для данного ряда) наблюдений. Аномальные наблюдения проявляются в виде сильного изменения уровня - скачка или спада - с последующим приблизительным восстановлением пре­дыдущего уровня. Наличие аномалии резко искажает результаты моделирования. Поэтому аномальные наблюдения необходимо ис­ключить из временного ряда, заменив их расчетными значениями.

Устойчивость характеризуется преобладанием закономернос­ти над случайностью в изменении уровней ряда. На графиках устойчивых временных рядов закономерность прослеживается визуально, на графиках неустойчивых рядов изменения последо­вательных уровней представляются хаотичными, и поэтому по­иск закономерностей в формировании значений уровней таких рядов лишен смысла.

Требование полноты данных обусловливается тем, что законо­мерность может обнаружиться лишь при наличии минимально допустимого объема наблюдений.

3.1 .2. Этапы построения прогноза по временным рядам

Экстраполяционное прогнозирование экономических процессов, представленных одномерными временными рядами, сводится к выполнению следующих основных этапов:

1) предварительный анализ данных;

2) построение моделей: формирование набора аппроксимирую­щих функций (кривых роста) и численное оценивание пара­ метров моделей;

3) проверка адекватности моделей и оценка их точности;

4) выбор лучшей модели;

5) расчет точечного и интервального прогнозов.

1. Предварительный анализ данных.

На этом этапе производится:

• выявление аномальных наблюдений;

• проверка наличия тренда;

• сглаживание временных рядов;

• расчет показателей развития динамики экономических про­цессов.

Так как наличие аномальных наблюдений приводит к искажению результатов моделирования, то необходимо убедиться в ­отсутствии аномалий данных. В качестве примера аномалии может служить скачок курса доллара, зафиксированный в «черный вторник».

Для диагностики аномальных наблюдений разработаны раз­личные критерии, например метод Ирвина [1]. Для всех или только для подозреваемых в аномальности наблюдений вычисляется величина λ_t: , где , .

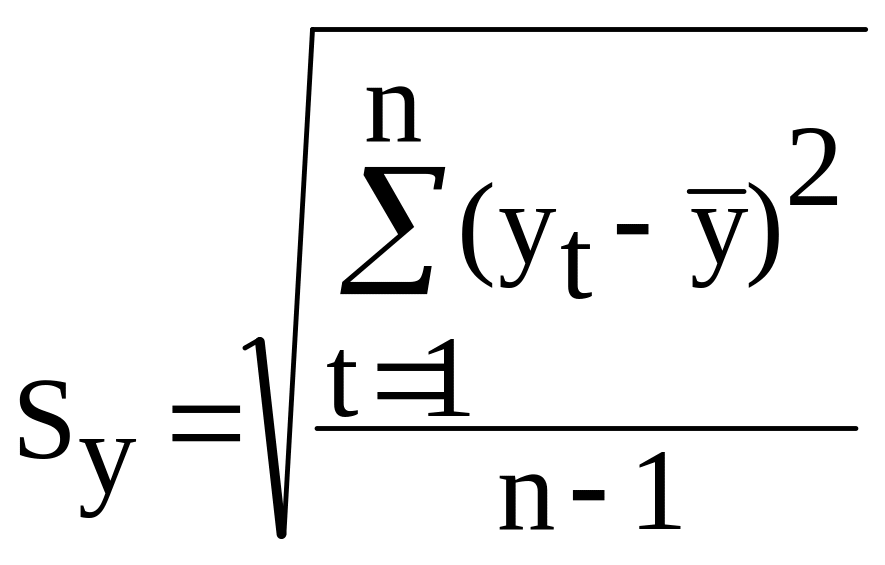Если рассчитанная величина λ_t превышает табличный уровень (например, для 10 наблюдений значение критерия Ирвина рав­но 1,5), то уровень y_t считается аномальным. Аномальные наблю­дения необходимо исключить из временного ряда и заменить их расчетными значениями (самый простой способ замены - в каче­стве нового значения принять среднее из двух соседних значений).

Следующая процедура этапа предварительного анализа, дан­ных - выявление наличия тенденций в развитии исследуемого по­казателя. Отметим, что тенденция прослеживается не только в увеличении или уменьшении среднего текущего значения времен­ного ряда, но она присуща и другим его характеристикам: диспер­сии, автокорреляции, корреляции с другими показателями и т.д. Тенденцию среднего визуально можно определить из графика исходных данных, а более точно - с помощью метода Фостера­ Стьюарта, метода проверки существенности разности средних и т.п., подробное описание которых дано в работе [1].

Наличие тенденции среднего уровня на графике становится более заметным, когда на нем отражены сглаженные значения исходных данных.

Процедура сглаживания необходима при построении некото­рых математических моделей и для устранения аномальных на­блюдений. Чаще всего для сглаживания применяются методы простой скользящей средней, взвешенной скользящей средней и экспоненциального сглаживания.

Традиционными показателями, характеризующими развитие экономических процессов, были и остаются показатели роста и прироста. Для характеристики динамики изменения экономических показателей все чаще используется понятие автокорреляции, которая характеризует не только взаимозависимость уровней од­ного и того же ряда, относящихся к разным моментам наблюде­ний, но и степень устойчивости развития процесса во времени, величину оптимального периода прогнозирования и т.п.