Решение

1. Воспользовавшись формулой (2.11) и результатами примера 2.1, находим коэффициенты прямой трудоемкости:

t₁ = 1160/775,3 = 1,5; t₂ = 460/510,1 = 0,9; t₃ = 875/729,6 = 1,2.

2. По формуле (2.15), где В - это матрица коэффициента пол­ных материальных затрат, найденная в примере 2.1, находим коэффициенты полной трудоемкости:

.

3. Умножая строки 1-3 первого и второго квадрантов межотрас­левого материального баланса, построенного в примере 2.1, на соответствующие коэффициенты прямой трудоемкости, полу­чаем схему межотраслевого баланса труда (в трудовых измери­телях) (табл. 2.4).

Таблица 2.4. Межотраслевой баланс затрат труда

Производящие отрасли		Потребляющие отрасли
		Межотраслевые затраты овеществленного труда						Затраты труда на конечную продукцию		Затраты труда в отраслях (трудовые ресурсы)
		1		2		3
1	348,0		76,3		437,5		299,2		1160,0
2	139,8		230,0		0,0		90,2		460,0
3	279,0		61,2		175,0		359,8		875,0

2.3. Модель международной торговли (линейная модель обмена)

В модели международной торговли процесс взаим­ных закупок товаров анализируется с использованием понятий собственного числа и собственного вектора матрицы А. Будем по­лагать, что бюджеты n стран, которые мы обозначим соответствен­но x_l, x₂, ..., x_n, расходуются на покупку товаров. Обозначим:

x_i - национальный доход страны i;

а_ij - доля национального дохода страны j, которую она рас­ходует на закупку товаров страны i;

p_i - общая выручка страны от внутренней и внешней тор­говли.

Предположим, что государство расходует весь свой нацио­нальный доход на закупку товаров внутри страны и на импорт из других стран. Это означает, что , j = 1, ..., n.

Матрица А, элементами которой являются коэффициенты а_ij, называется структурной матрицей торговли. Сумма элементов каждого столбца этой матрицы равна единице.

Предположим, что в течение некоторого фиксированного про­межутка времени не меняется структура международной торговли (т.е. структурная матрица торговли остается постоянной), тогда как национальные доходы торгующих стран могут измениться. Тре­буется определить, какими могут быть национальные доходы, чтобы международная торговля осталась сбалансированной, т.е. что­бы сумма платежей всех государств была равна суммарной выручке от внешней и внутренней торговли.

Для любой страны выручка от внутренней и внешней торгов­ли составит

p_i = a_i1x₁ + a_i2x₂ + ... + a_inx_n, I

В сбалансированной системе международной торговли не должно быть дефицита, т.е. у каждой страны выручка от торговли должна быть не меньше ее национального дохода: p_i ≥ x_i, i = 1, 2, ..., n.

Последнее неравенство справедливо только в случае, когда p_i = x_i, i = 1, 2, ..., n, т.е. у всех торгующих стран выручка от внешней и внутренней торговли должна совпадать с национальным доходом [4]. В матричной записи это означает, что имеет место равенство АХ = Х, где А - структурная матрица международной торговли, а Х - вектор национальных доходов.

Вектор Х является собственным вектором структурной матри­цы торговли А, а соответствующее собственное значение равно единице. Отсюда следует, что баланс в международной торговле будет достигнут, если собственное значение структурной матрицы международной торговли равно единице, а вектор национальных доходов торгующих стран является собственным вектором, отве­чающим этому единичному собственному значению.

Пример 2.3. Найти национальные доходы X₁, Х₂, Х₃ торгующих стран в сбалансированной системе международной торговли. Структурная матрица торговли трех стран имеет вид: .
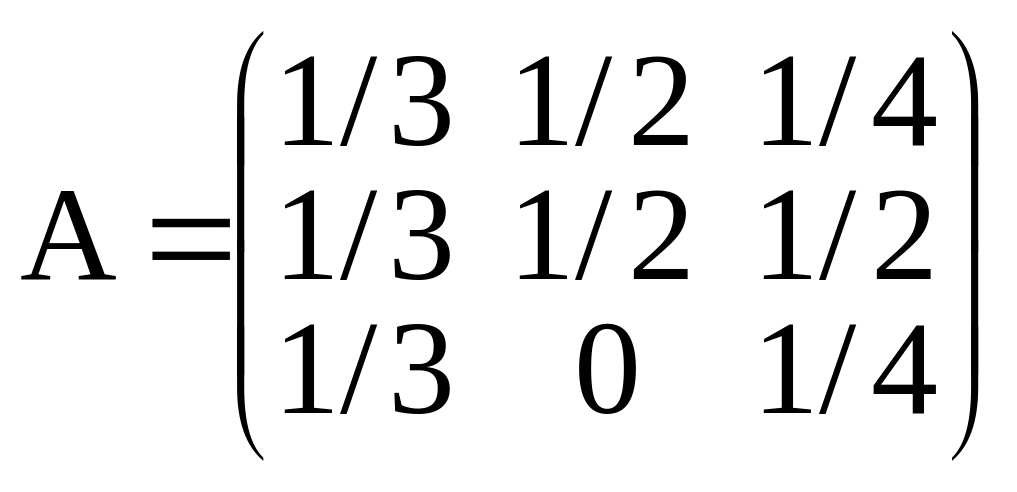