П одставляя в это выражение момент движущий

получим:

С учётом М_Н=Const (давление нагнетания Р_н поддерживается постоянным гидродинамически разгруженным клапаном) рабочий режим системы ТТГГ-ГМ определяется в точке «О» пересечением механической и нагрузочной характеристик

М

О



Рис. 23 Механическая характеристика ТТГГ и ГМ

Точка «О» является точкой устойчивого равновесия и свидетельствует о параметрах М,  режима совместной работы ТТГГ и АПМНА.

2.3.2. Геометрические и объёмные характеристики

Удельные объёмные расходы за оборот ГМ и ГН находятся из суммарных объёмных характеристик, которые являются конструктивными параметрами газового мотора и насоса с учётом особенностей конструктивного исполнения газового и гидравлического распределителей. Если для гидравлического насоса q_н – паспортная величина, то для газового мотора необходимо при согласовании характеристик с ТТГГ проведение подробного расчёта q_м. Расчётная схема q_м представлена на рис. 24

Рис. 24 Распределитель газа АПМНА.

Как было изложено ранее, работа ТТГГ в составе с ГМ характеризуется переменной площадью эффективного критического сечения, образованного при наложении отверстий вращающегося блока цилиндров на прорезь, выполненную в газораспределителе, для участка впуска газа в поршневую полость в цикле расширения объёма (рис. 24) Отверстие впуска образуется в результате пересечения цилиндрического отверстия блока цилиндров с серпообразным каналом распределителя газа.

Газоприход от ТТГГ расходуется в ГМ на:

-заполнение переменного поршневого объёма блока цилиндров, находящегося в просвете серпообразного канала ( );

-заполнение через переменное проходное сечение «начального объёма при подключении очередного цилиндра к серпообразному каналу в зоне неизменного объёма под поршнем – нижняя «мертвая точка» ( );

-непроизводительные утечки через зазоры между поршнями и гильзами блока цилиндров, находящихся в просвете серпообразного канала, и через зазор между рабочим торцом блока цилиндров и зеркалом распределителя газа ( ).

Таким образом, уравнение баланса массового секундного расхода газа для ТТГГ и ГМ записывается в следующем виде:

Н а рис. 25 построены кривые изменения объёмов от угла поворота блока цилиндров «а» по каждому плунжеру (всего их 7) и суммарная объёмная характеристика «б» газового мотора от угла поворота вала для угла отсечки = 52 газового распределителя.

V_i V_

10





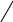
5

Рис. 25 Объёмные характеристики газового мотора

Графики строились по выражению, справедливому для одного цилиндра:

где:

- относительный текущий объём;

V _o- начальный объём;

-максимальное значение относительного объёма.

Как следует из графика V=f(), средний объёмный расход газа по углу составляет dV_ср/d=tg. Минимальный массовый расход по углу , характеризуемый изломом кривой суммарной характеристики и получаемый в результате выхода отверстия блока цилиндров из просвета серпообразного канала (рис. 25), составляет dV_ср/d=tg.

2.3.3.Расчёт индикаторной диаграммы – характеристики эффективности газового мотора

Энергетические показатели газового мотора, его рабочий цикл определяются индикаторной диаграммой каждого поршня, который производит работу за счёт расширения подпоршневого объёма. Индикаторная диаграмма строится в плоскости «давление – объём». Степень совершенства рабочего цикла оценивается полнотой индикаторной диаграммы, другими словами, интегралом (площадью) под кривой давления, а также, минимизацией потерь механической энергии в процессе впуска газа в полость силового цилиндра. Чем больше площадь, тем большую работу совершает поршень.

В работе [Труханов Г.А. Исследование рабочего процесса теплового двигателя бортовой питающей установки, диссертация к.т.н., ЦНИИ АГ, 1970г.] показано, что оптимальным для режима работы газового двигателя в диапазоне частот вращения 6000…10000 об/мин является круглое отверстие впуска с диаметром ~4,5 мм.

При составлении расчётной методики использованы методы расчёта динамики глухих камер для турбулентных и ламинарных дросселей. Все выводы проводятся при двух общих допущениях.

Неустановившиеся процессы течения газа через переменный дроссель рассматриваются как квазистатические, т. е. принимается, что в переходном процессе в каждый момент времени мгновенное значение расхода газа через дроссель такое же, каким оно было бы при данной разнице давлений в условиях установившегося течения; действие сил инерции, неучтённое при введении этого допущения, приводит к запаздываниям, характеризуемых постоянными времени, обычно несоизмеримо малыми в сравнении с постоянными времени, обусловленными ёмкостью камер.

Предполагается, что изменение состояния газа в полости блока цилиндров подчинено адиабатическому закону; в действительности при переходных процессах чаще всего состояние некоторой массы газа в полости не следует закону адиабаты, и обычно для камер рассматриваемых типов процессы изменения состояния являются промежуточными между адиабатическими и изотермическими процессами. Однако разница между временами заполнения и опорожнения полостей при изотермическом и адиабатическом изменениях состояния газа в полости невелика.

При получении выражений для построения индикаторной диаграммы ГМ следует различать полости с дросселями турбулентными (истечение газа через переменное отверстие блока цилиндров) и ламинарными (истечение газа через кольцевой зазор между плунжером и блоком цилиндров).

Алгоритм расчёта охватывает расчёт для трёх циклов индикаторной диаграммы:

1. Цикл заполнения полости через дроссель переменного сечения при переменном расширении объёма.

2. Цикл расширения и опорожнения через торцовый и кольцевой зазоры.

3. Цикл опорожнения через переменное выхлопное отверстие.

2.3.4. Рабочий цикл впуска газа в переменный объём при переменном сечении входного отверстия

Для получения характеристик заполнения и опорожнения будем пользоваться расчётной схемой, представленной на рис. 26

f( t)

Р_к, V( t)

Р ₁

V

V _o

_отс _вых t

+

+

+ =t

Рис. 26 Расчётная схема цикла впуск газа

Считая, что заполнение полости цилиндра происходит при Р₁=const (игнорируются высокочастотные пульсации с малой амплитудой), и учитывая, что температура газа Т=const, получим из характеристического уравнения выражение для изменения параметров в полости:

В ыражение для изменения массы газа в полости имеет вид:

из которого следует зависимость для массового расхода газа:

С другой стороны, в соответствии с формулой для массового расхода имеем:

где для докритического и сверхкритического истечений значения комплекс (r) записывают в следующем виде:

г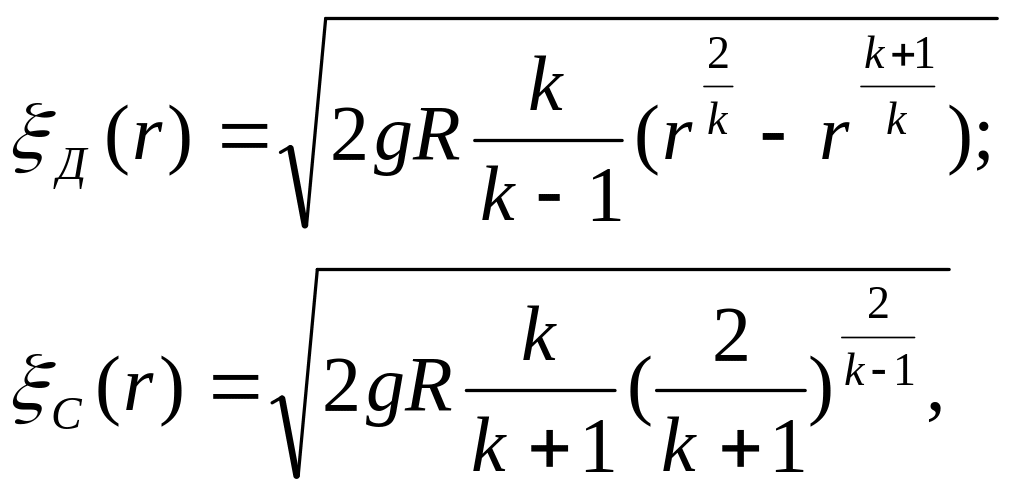 де:

r=P_К/Р₁ – относительное давление в полости цилиндра; k – показатель адиабаты; R – газовая постоянная; V(t) – величина текущего значения объём полости блока цилиндров; f(t) – величина текущего значения площади проходного сечения для газа;  - коэффициент расхода газа; Т – абсолютная температура.

П риравняв правые части выражений для массового секундного расхода и разделив переменные r и t, получаем:

Считаем с погрешностью < 5…7%, что f(t)=k_ft,

где:

n – обороты в минуту газового мотора,

f_max – максимальная площадь отверстия в блоке цилиндров,

 - угловой размер (растр) отверстия в блоке цилиндров для впуска газа в полость,

V_o – “начальный” объём полости ГМ,

V_max – максимальный объём, образуемый при движении поршня,

d_ц – диаметр поршня,

D_б – диаметр делительной окружности положения поршней блока цилиндров,

 - угол наклона оси выходного вала ГМ к оси вращения блока цилиндров.

Для t <60 Cost ~1-(t )²/2. Подставив f(t)=k_ft и V(t) в последнее равенство, получим:

где:

Подставив функцию _с(r) для сверхкритического истечения в полость ГМ и выполнив интегрирование левой и правой частей дифференциального уравнения в пределах 0…t и r_o…r_кр, получим:

где:

• о тносительное начальное давление в полости цилиндра, равное относительному давлению выхлопа газа,

r_кр – относительное критическое давление в полости цилиндра.

Интегрируя правую и левую части, получим:

Преобразование полученного соотношения позволяет получить зависимости давления в полости блока цилиндров от времени t (или угла ) для сверхкритического истечения газа в полость в виде:

Для определения времени заполнения полости при сверхкритическом истечении следует в t_зc подставить относительный критический перепад давления

Для нахождения зависимости давления от времени при докритическом перепаде между входным давлением и относительном критическом перепаде давления необходимо комплекс _Д(r) подставить в исходное выражении. В результате имеем:

После интегрирования получаем:

откуда:

Подстановка r=1 , при котором уравниваются давления на входе и в полости и прекращается заполнение полости, получаем время заполнения полости при докритическом перепаде давления.

Полное, суммарное время заполнение полости ГМ находят сложением соответствующих времён при сверхкритическом и докритическом перепаде:

2.3.5. Рабочий цикл расширения газа при переменном объёме полости блока цилиндров

Цикл опорожнения полости газового мотора после отсечки от отверстия впуска до подхода блока цилиндров к отверстию выхлопа происходит через кольцевой зазор, образуемый между полостью и двигающимся поршнем (рис.), при увеличивающемся, по мере поворота ГМ, объёме полости.



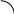
Рис.27 Расчётная схема цикла расширения

Для полости с движущимся поршнем дифференциальное уравнение имеет вид:

где:

- проводимость кольцевого зазора; d_ц – диаметр поршня;  - кольцевой зазор в плунжерной паре, =(374+5,03Т)10^-12 Нс/см² – динамическая вязкость газа; l – длина плунжера.

Разделив переменные, произведём интегрирование в пределах Р_t…P_к:

где Р_t – текущее значение давления (Р_t<Р_к) или в безразмерном виде r= Р_t/Р_к.

Обозначив V_o/k_V+1=a>1, получим:

Откуда выражение для определения времени (или угла), при котором происходит опорожнение полости блока цилиндров, для случая истечения газа через ламинарный дроссель (зазор) имеет вид:

Так как t - угол поворота блока цилиндров относительно распределителя газа является геометрическим размером, то подставив  в t_ОП, можно определить давление газа в полости ГМ к моменту выхлопа.

2.3.6. Рабочий цикл на выхлопе газа из газового мотора

После окончания цикла расширения газа при его истечении через зазор наступает цикл выхлопа газа из полости в выхлопную магистраль (рис. 28).

Рис. 28 Расчётная схема цикла выхлопа газа.

Так как угол, при котором опорожняется полость мал =t<14, то V(t)=Const и Cost=1, а объём полости достигает максимальное значение и вычисляется по соотношению:

Полагая r=Pвых/Рк=Const, имеем

Подставляя последнее равенство в характеристическое уравнение dG=(V/RT)dP_к, записываем следующее дифференциальное уравнение, описывающее процесс изменения давления в цикле выхлопа газа из ГМ:

Тогда уравнение истечения газа из полости газового мотора

и меет вид:

Для сверхкритического перепада давления, когда r_кр<0,5, преобразованное дифференциальное уравнение имеет вид:

В пределах интегрирования t=0…t, r=1…r_кр время опорожнения вычисляется по выражению:

Для докритического перепада давления между полостью и магистралью выхлопа, когда r_кр>0,5, дифференциальное уравнение имеет вид:

Интегрирование правой части для произвольных «k» не производится. Произведём эту операцию для горячего газа k=1,25 и воздуха k=1,4.

Для горячего газа в пределах интегрирования 0…t и r_кр…r_o=1 время опорожнения определяется по выражению:

где:

а Ф(r_кр) определяется в результате подстановки r_кр в Ф(r).

Для воздуха в пределах интегрирования 0…t и r_кр…r_o=1 время опорожнения определяется по выражению:

где:

В ремя полного опорожнения полости определяется равенством:

Таким образом, построение индикаторной диаграммы давления в полости блока цилиндров состоит в припасовке соответствующих циклов диаграммы. Качественнная картина индикаторной диаграммы представлена на рис. 29

P

V

Рис. 29 Индикаторная диаграмма газового мотора

- реальная диаграмма,

- идеальная диаграмма.

Разница в площади идеальной S_и и реальной S_p диаграмм свидетельствует об эффективности, совершенстве газового цикла в газовом моторе. Объёмный КПД определяется по соотношению

Место для формулы.

Для разработанного ряда газовых моторов объёмный КПД составляет K_Q=0,7…0,8.

2.3.7. Оценка влияния пульаций давления, источником которой является вращающийся блок цилиндров, на работу ТТГГ.

Совместная работа ТТГГ и ГМ характеризуется наличием пульсаций давления на входе в газовый мотор, появляющихся в результате отсечки отверстия впуска газа в полость ГМ от ТТГГ.

Считая, что основная часть газоприхода идёт на заполнение полости поршня (только 20…25% затрачивается на непроизводительные утечки) целесообразно рассмотреть влияние пульсаций давления в полости ГМ на работу ТТГГ.

Ч астота появления в просвете газовода переменных объёмов полостей цилиндров, а, следовательно, частота изменения расхода обусловлена скоростью вращения блока цилиндров в соответствии с механической характеристикой энергоблока ТТГГ-ГМ и может быть рассчитана по соотношению

где:

z – количество поршней блока цилиндров;

 - угловая скорость вращения блока цилиндров.

Для наглядности представления расчётной методики оценки пульсаций целесообразно использовать расчётную схему, представленную на рис. 30:



Рис. 30 Расчётная схема пульсаций давления

При выводе уравнений приняты следующие допущения:

• продукты сгорания твёрдого топлива подчиняются уравнению состояния для идеального газа;

• температура газа и перепад давления на фильтре постоянны.

У равнение сохранения массы для камеры сгорания 1 заряда имеет вид:

где V-свободный объём камеры сгорания заряда, Р₁-давление газа в камере сгорания, m_рас-массовый секундный расход газа.

Расход газа через фильтр 2 при докритическом перепаде давления между камерой сгорания 1 и газоводом 3 (Р₂/Р₁>0,5) определяется выражением:

где ₁-площадь эффективного сечения, которое представляет собой фильтр, обеспечивающий перепад давления Р= Р₂-Р₁, давление Р₂-давление в газоводе.

После подстановки уравнение состояния будет иметь вид:

Дифференциальное уравнение нелинейно. Проведение линеаризации правой части в окрестности установившихся параметров Р₁₀, Р₂₀ разложением в ряд Тейлора и отбрасывание членов второго порядка малости даёт погрешность результата динамики процессов не превышающей 10…12%.

Линеаризация первого члена правой части приводит к результату в виде:

Линеаризацию второго члена следует провести по двум переменным Р₁ и Р₂, при этом:

где:

Подставив линеаризованные члены уравнения в уравнение расхода, получим линейное дифференциальное уравнение первого порядка для оценки давления в камере сгорания:

Используя преобразование Лапласа, получим передаточную функцию, как реакцию давления в камере сгорания на изменение давления в газоводе:

Для апериодического звена первого порядка амплитудно-частотная характеристика имеет вид:

График АЧХ представлен на рис. 31 для следующих параметров: k=1,25; =0,5; u₁=0,03; =1,55*10^-3 кГ/см³; S=35,7 cм²; Р₁₀=6 Мпа; Р₂₀=5,5 МПа; ₁=0,232 см²; R=4000 кГсм/(кг·К); Т=1400 К; V=500 cм³; А₁·ξ=-0,62; А₂·ξ =-0,467.

А()

1,0

45

0,75

0,5

0,25

 [рад/с]

0 25 50 75 100

Рис. 31 АЧХ ТТГГ при изменении частоты давления Р₂

Из графика следует, что амплитуда колебаний давления в камере ТТГГ при возмущении в газоводе колебаний давления на частотах  близких к 0 составляет 0,77 изменения в газоводе. При увеличении частоты колебаний в газоводе в диапазоне 5…50 рад/с происходит падение коэффициента передачи колебаний до ~ 25%, а при рабочих частотах >100 рад/с ослабление амплитуды становится пренебрежимо мало.