Глава XVII. Переменный ток

§ 151. Постоянная и переменная электродвижущая сила.

В генераторах электрического тока, с которыми мы зна­комились до сих пор — электростатических машинах, гальванических элементах (§ 75), аккумуляторах (§ 79) и термоэлементах (§ 83),— э. д. с. с течением времени не меняла своего направления: положительный электрод всегда оставался положительным, отрицательный — отри­цательным, и ток во внешней цепи постоянно шел в одном и том же направлении: от положительного электрода к отрицательному. Такой ток называют прямым или постоян­ным. До тех пор, пока не происходило никаких внутренних изменений в самом генераторе, т. е. пока не сказывались, например, явления поляризации электродов в гальваниче­ских элементах, или -не менялась скорость вращения электростатической машины, или не менялась температура между спаями термоэлемента, оставалась постоянной и э. д. с., а стало быть, и напряжение на зажимах генера­тора и сила тока в цепи.

Напротив, в генераторах, установленных на элект­ростанциях и дающих ток, которым мы пользуемся для освещения, приведения в действие электродвигателей (мо­торов) и для других целей, всегда возникает переменная э. д. с., непрерывно изменяющая свое значение и много раз в секунду меняющая свое направление. С некоторыми деталями устройства этих генераторов мы познакомимся в следующей главе, но для понимания того, каким образом в них создается переменная э. д. с., нам необходимо уже сейчас выяснить основной принцип их устройства.

В современной технике применяются почти исключи­тельно индукционные генераторы, т. е. машины, в кото­рых э. д. с. возникает в результате процесса электромаг­нитной индукции. Основная схема устройства такого ге­нератора, на которой видны все принципиально важные его детали, показана на рис. 288. Между полюсами силь­

ного магнита 1, т. е. в магнитном поле, вращается прово­лочная рамка 2^ концы которой припаяны к кольцам 3 и 4, вращающимся вместе с рамкой; к $тим кольцам прижи­маются пружинящие пластинки 5 и 6 (так называемые щетки), от которых идут провода к внешней цепи. При вращении рамки в магнитном поле пронизывающий ее

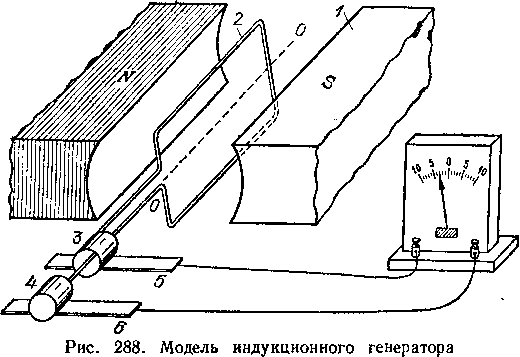
магнитный поток все время изменяется и, следовательно, в рамке возникает индуцированная э. д. с. Таким образом, процесс, происходящий во всех промышленных генераторах тока, это — повторение в гигантских масштабах основного индукционного опыта Фарадея, который мы рассмотрели в § 138. .

Рассмотрим теперь подробнее, какова будет возникаю­щая в рамке индуцированная э. д. с. Для простоты будем считать магнитное поле, в котором вращается рамка, однородным. Магнитный поток через рамку Ф (§ 138) есть произведение магнитной индукции поля на площадь рамки и на синус угла q> между плоскостью рамки и на­правлением поля:

Ф = BS sin ф.

Если рамка вращается равномерно и совершает полный оборот за время Т, то за единицу времени рамка повора­чивается на угол 2п/Т. Поэтому, если время отсчитывать от того момента, когда рамка стояла параллельно линиям поля, то значение угла <р в некоторый момент времени t будет равно q>= (2n/T)t. Обозначая частоту вращения

рамки, т. е. число ее оборотов в единицу времени, буквой v, а угловую скорость (см. том I) буквой ю, можно написать;

1. о 2л

v = y » ^w = 2nv = y •

Стало быть,

Ф = tot.

Подставив это выражение в формулу для магнитного потока, мы увидим, что закон его изменения с течением времени имеет вид

Ф — BS s'mat. (151.1)

График, изображающий зависимость магнитного потока через рамку от времени, представляет собой синусоиду

Рис. 289. График изменения с течением времени мгновенных значений: а) магнитного потока Ф; б) индуцированной*э. д. с. в опыте, изоб­раженном на рис. 288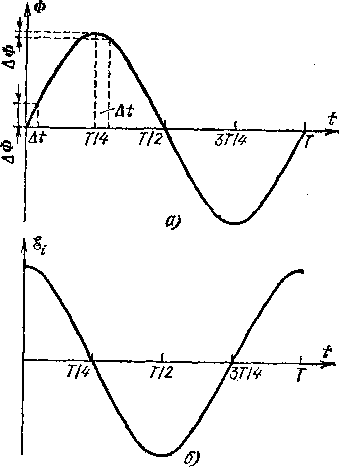

(рис. 289, а). Магнитный поток меняет свой знак два раза за каждый оборот рамки, обращаясь в нуль в те моменты, когда она параллельна направлению поля, и достигая максимальных значений (того или иного знака) в моменты, когда она перпендикулярна к полю.

Индуцированная в рамке э. д. с. определяется не зна­чением самого магнитного потока, а скоростью его изме­нения, т. е. величиной ДФ/Д/ (§ 141). Нетрудно видеть, что и эта величина не остается постоянной, а все время изменяется при вращении рамки. На рис. 289, а показаны изменения магнитного потока ДФ за одинаковые проме­жутки времени Д/ для момента t—0, когда Ф=0, и для момента /=774, когда Ф имеет максимальное значение. Первое значение ДФ гораздо больше второго, и, следова­тельно, мгновенное значение индуцированной э. д. с. в момент /=0 имеет максимальное значение, а по мере вра­щения рамки убывает, достигая нулевого значения к мо­менту 774.

При дальнейшем повороте рамки э. д. с. меняет свой знак. Действительно, по правилу Ленца (§ 139) индуци­рованная э. д. с. всегда направлена так, чтобы магнитное поле создаваемого ею тока тормозило процесс, вызыва­ющий индукцию. Поэтому в течение первой четверти пе­риода, когда магнитный поток через рамку возрастает, поле индукционного тока должно ослаблять внешнее поле, а в течение следующей четверти периода, когда магнитное поле убывает, оно должно усиливать это поле. Отсюда ясно, что в моменты прохождения э. д. с. через нуль долж­но происходить изменение ее знака.

На рис. 289, б графически показана зависимость мгно­венных значений индуцированной э. д. с. от времени. Можно показать, что эта кривая, как и график магнитного потока, представляет собой синусоиду, но только смещен­ную на четверть периода по отношению к синусоиде, изоб­ражающей изменение магнитного потока.

Действительно, для момента t поток Ф— BS sin Ш, для момента t-\-At поток®'=SS sin ш(Н-Д<). Следовательно, за время At изменение потока

Дф = ф'— <D = BS [sin со (£-)- ДО—sin ш<].

Согласно известной теореме тригонометрии это выражений можно пред­ставить в виде

A® = 2SScos [ш ^slп‘lГ”•

Если At оченьмало, то sin (шД£/2)=а>Д//2, a cos[w(H-A//2)]=cos <at. Итак, изменение потока за малое время At

ДФ = BSa> cos (ot-At.

Следовательно, э. д. с., равная —ДФ/Дt, есть

ДФ / jr \

8{ = — —=— BSacosat — BSasin f са^ —g- J ,

т. е. действительно выражается синусоидой той же частоты, но сдви­нутой на л/2 (четверть периода) ¹).

Само собой разумеется, что по такому же закону си­нусоиды изменяется и мгновенное значение напряжения и на зажимах машины или между двумя любыми точками сети. Графики изменения этой величины имеют такой же вид, как и приведенные на рис. 289 графики индуциро­ванной э. д. с. Говорят, что такого рода кривые воспроиз­водят «форму» переменного напряжения. Ток, возникающий под влиянием переменного напряжения, также будет пере­менным, и «форма» его подобна «форме» напряжения.

Не только в нашей модели, но и в машинах, применя­емых в электротехнике, в подавляющем большинстве слу­чаев имеют дело с напряжениями и токами, которые можно считать синусоидальными. Закон изменения мгновенных значений этих величин со временем выражается формулами

u = U_msm^t, i = I_m sin со/, (151.2)

причем через U_m и 1_т обозначены максимальные значения напряжения и тока.

§ 152. Опытное исследование формы переменного тока. Осциллограф. В том,, что ток, получаемый от электростан­ций, является действительно переменным, т. е. много раз в секунду меняет свое направление, нетрудно убедиться с помощью такого простого опыта. Включим в сеть обыч­ную электрическую лампочку и осторожно поднесем к ней постоянный магнит так, чтобы нить лампочки была пер­пендикулярна к линии его магнитного поля. Мы увидим, что при этом нить лампочки расплывается в широкую полоску. Это показывает, что нить в поле магнита быстро колеблется, отклоняясь то в одну сторону, то в другую. Но мы знаем, что в постоянном магнитном поле ток опре­деленного направления отклоняется в одну сторону. Сле­довательно, наш опыт показывает, что ток в нити лам­почки меняет свое направление много раз в секунду.

Этот простой опыт хотя показывает нам, что ток в сети — переменный, но не дает еще возможности просле­дить за законом изменения мгновенных значений силы тока, т. е. изучить его форму. Если бы в опыте на рис. 288 мы вращали рамку достаточно медленно, то увидели бы,

что стрелка гальванометра во внешней цепи рамки откло­няется то в одну сторону, то в другую. Следя за отклоне­ниями его стрелки, мы могли бы составить себе некоторое представление и .о форме этого тока. Однако технический переменный ток меняет свое направление настолько часто, что обычные гальванометры уже не успевают следить за его изменениями, потому что подвижная часть их (рамка) обладает слишком большой инерцией. Для изучения формы технического переменного тока и токов еще большей ча­стоты нужны приборы более «послушные». Такие приборы, предназначенные для исследования быстропеременных то­ков и напряжений, называются осциллографами.

Рис. 290. Устройство петлевого осциллографа: 1 — петля осцил­лографа, обтекаемая перемен­ным током, 2 — зеркальце, при­клеенное к петле, поворачиваю­щееся вокруг оси 00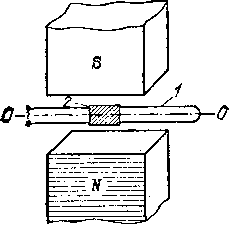

Устройство простого осциллографа показано на рис. 290. По существу — это обычный зеркальный гальванометр, но только рамка его, поворачивающаяся в магнитном

*1

Рис. 291. Схема наблюдения зайчи­ка, отбрасываемого зеркальцем ос­циллографа: 1 — источник света,

2. — направляющая линза, 3 — зер­кальце, 4 — вращающийся зеркаль­ный барабан, 5 — экран

поле, и зеркальце, с помощью которого мы следим за от­клонениями рамки, сделаны чрезвычайно легкими. Рамка осциллографа часто представляет собой просто петлю из очень тонкой проволоки, подвешенную на упругих рас­тяжках в поле магнита ¹). Когда пропускают через эту рамку переменный ток, то она, а вместе с ней и зеркальце начинают быстро колебаться; отраженное от зеркальца световое пятно («зайчик») быстро движется по экрану то в одну сторону, то в другую, выписывая на нем прямую линию, перпендикулярную к оси вращения зеркальца.

Для того чтобы с помощью этого прибора получить кривую, изображающую форму тока, луч света, отраженный от зеркальца, направляют не прямо на экран, а заставляют сначала отразиться от зеркала, которое быстро вращается вокруг оси, совпадающей с направлением движения зай­чика. Вместо простого вращающегося зеркала удобно взять барабан с зеркальными гранями, благодаря чему луч света имеет возможность за время одного оборота ба­рабана отразиться поочередно от каждой из его зеркаль­ных граней. Такое расположение приборов показано на рис. 291. Здесь ось зеркальца горизонтальна, а барабан вращается вокруг вертикальной (перпендикулярной к плоскости чертежа) оси. Повороты зеркальца смещают положение зайчика на экране вверх и вниз, а вращение барабана смещает его влево или вправо. Ясно, что при сложении этих движений зайчик будет выписывать на экране некоторую кривую. При этом смещение зайчика по вертикали пропорционально мгновенному значению силы тока через прибор, а смещение его по горизонтали пропорционально времени, так как. барабан вращается равномерно. Таким образом, полученная кривая изобра­жает форму переменного тока. Опыт показывает, что для технического тока эта кривая действительно очень близка к синусоиде. Такой же вид имеют и кривые, изображающие форму технического переменного напряжения.

Описанное расположение приборов применяется преимущественно в демонстрационных опытах для того, чтобы наглядно показать форму переменного тока. На практике при исследованиях переменного тока обычно барабан делают цилиндрическим и надевают на него фотогра­фическую бумагу, на которой луч прямо выписывает соответствующую кривую.

Еще более широкое распространение получили в настоящее время так называемые электроннолучевые осциллографы ¹). Главной частью этих приборов является уже знакомая нам электроннолучевая трубка (рис. 182). На горизонтальные пластины трубки подается напряжение, пропорциональное исследуемому току. Таким образом, отклонение луча по вертикали или смещение по вертикали яркого пятнышка на экране трубки в каждый момент времени пропорционально мгновенному значе­нию тока. На вертикальные же пластины с помощью специального уст­ройства подают напряжение, которое равномерно нарастает от нуля до некоторого максимального значения, затем очень резко, практически «мгновенно», падает до нуля, снова равномерно нарастает и т. д. Форма такого «пилообразного» напряжения показана на рис. 292. При наложе­нии такого напряжения пятнышко на экране осциллографа движется по горизонтали, затем «сразу» возвращается в исходное положение, снова пробегает тот же горизонтальный отрезок и т, д.

Очевидно, что при одновременном действии исследуемого напряже­ния, наложенного на горизонтальные пластины осциллографа, и «пи­лообразного» напряжения на его вертикальных пластинах светящаяся точка на экране будет вычерчивать кривую, дающую форму исследуе­мого напряжения или тока, Электроннолучевой осциллограф является

и

Рис, 292. «Пилообразная» форма на­пряжения, накладываемого на верти­кальные пластины электроннолучевого осциллографа для осуществления раз­вертки по оси времени

одним иа важнейших средств исследования переменных токов и напря­жений. Он чрезвычайно широко применяется в самых различных лабо­раториях, а также на ряде предприятий.

§ 153. Амплитуда, частота и фаза синусоидального пере­менного тока и напряжения. Рассмотрим подробнее кривую, изображающую зависимость мгновенного . значения тех­нического переменного тока (или напряжения) от времени (рис. 293). Прежде всего обращает на себя внимание тот

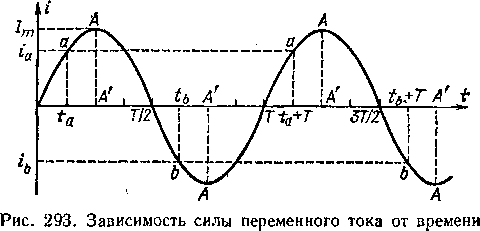
факт, что этот ток (или напряжение) изменяется перио­дически, т. е. каждое мгновенное значение этих величин, например значение, соответствующее точке а (или точке Ь), повторяется через один-и тот же промежуток времени. Другими словами, сила тока (или напряжение) пробегает за этот промежуток времени все возможные значения, возвращаясь к исходному, т. е. совершает полное коле­бание. Промежуток времени, в течение которого сила тока (или напряжение) совершает полное колебание и принимает прежнее по модулю и знаку мгновенное значение, называется периодом переменного тока. Его принято обозначать бук­вой Т. Для сетей СССР и большинства других стран Т— =1/50 с, а так как изменение направления тока проис­ходит два раза в течение каждого периода, то технический ток меняет свое-направление 100 раз в секунду.

Максимальное значение, которое может иметь перемен­ный ток (или напряжение) в том или другом направлении, называется амплитудой этой величины. На рис. 293 ам­плитуда изображается отрезками АА'. Амплитуду токов и напряжений обозначают /_т или {/_т, а их мгновенные значения —( и и.

Число полных колебаний (циклов^ синусоидального тока или напряжения за единицу времени называют ча­стотой соответствующей величины и обозначают буквой v ¹). Очевидно,

y=r- ^T = h 0S3.1,

За единицу частоты принимают частоту, равную одному колебанию в секунду. Эту единицу называют герцем (Гц) по имени немецкого физика Генриха Герца (1857—1894). Таким образом, технический переменный ток имеет частоту 50 Гц.

Вместо частоты v вводят также величину (o=2nv=2n/T, которую называют циклической или круговой частотой тока (напряжения). Она представляет собой число пол­ных колебаний (циклов) данной величины за 2л секунд.

Пока мы имеем дело только ■ с одним синусоидальным переменным током или переменным напряжением, частота и амплитуда являются полными и исчерпывающими ха­рактеристиками этих величин, потому что начальный момент отсчета времени мы можем выбрать произвольно. Но когда нам приходится сопоставлять друг с другом две или несколько величин такого рода, мы должны учитывать и тот факт, что они могут достигать максимального зна­чения не в один и тот же момент времени.

Две кривые на рис. 294, а изображают форму двух синусоидальных переменных токов с одной и той же ча­стотой и амплитудой, но кривые эти смещены по оси абс­цисс (оси времени) на отрезок, равный четверти, периода. Начальная точка отсчета времени выбрана так, что для первой кривой нулевые значения достигаются в моменты 0, Г/2, Т, ЗГ/2 . . ., а амплитудные — в моменты Г/4, ЗГ/4, 5Г/4, . . . Вторая же кривая проходит через нулевые значения в моменты Г/4, ЗГ/4, 5Г/4, . . ., а через ампли­тудные— в моменты Г/2, Г, ЗГ/2, ...

В подобных случаях говорят, что эти два тока (или две другие синусоидальные величины) сдвинуты друг относительно друга по фазе, или, иначе, что между ними существует некоторый сдвиг фаз (или разность фаз), рав­ный в данном примере четверти периода. Так как кривая /

Рис. 294. Графическое изображение переменных токов одинаковой ча­стоты и амплитуды, смещенных, по фазе: а) два синусоидальных тока, смещенные по фазе на четверть периода; 6) токи, изображаемые кривыми 2 и 3, смещены по фазе относительно кривой 1 на одну восьмую часть

периода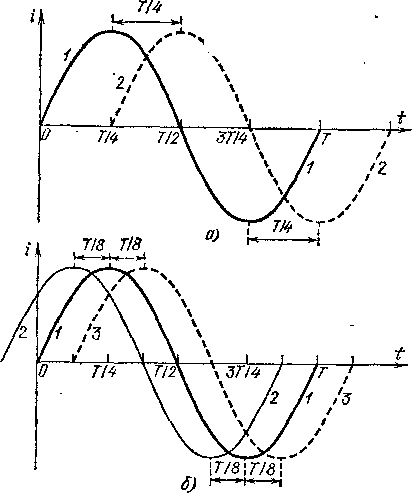

проходит через амплитудное значение, так же как и через любое другое соответствующее значение, раньше, чем кри­вая 2, то говорят, что она опережает кривую 2 по фазе или, иначе, что кривая 2 отстает по фазе от кривой 1.

л 153.1. На рис. 294, 6 кривые 2 и 3 сдвинуты относительно кривой

• 1 по фазе на одну восьмую периода. .Определите, какая из этих кривых отстает по фазе от кривой 1 и какая опережает ее. Какова разность фаз между кривыми 2 и 37

Во всех случаях, когда приходится сопоставлять си­нусоидальные величины или рассматривать их совмест­ное действие (складывать или < перемножать их),» вопрос о

соотношении фаз между этими величинами имеет очень важное значение. Таким образом, в общем случае, когда имеется несколько синусоидальных токов или напряже­ний, нужно характеризовать каждый из них тремя вели­чинами: частотой, амплитудой и фазой или, точнее, сдви­гом фаз между данным током (или напряжением) и каким-нибудь дру­гим, относительно которого мы рас­сматриваем сдвиг фаз всех осталь­ных.

осциллограф для одно­временной записи двух переменных токов, прохо­дящие через петли 1 к 2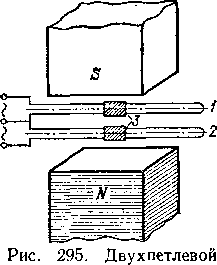

Соотношения между фазами раз­личных синусоидальных перемен­ных токов очень удобно изучать при помощи петлевого осциллогра­фа, имеющего в отличие от при­бора, описанного в § 152, не одну, а две отдельные рамки (петли), по­мещенные в общее магнитное поле (рис. 295). Развертка формы обоих токов, проходящих по этим пет­лям, по оси времени осуществляет­ся одним и тем же вращающимся барабаном, так что точки двух получающихся на экране кривых, расположенные друг над другом, изображают мгновенные значения сравниваемых токов, соответствую­щие одному и тому же моменту времени.

Точное математическое определение фазы синусоидальной перемен­ной величины (тока или напряжения) таково. Мгновенное значение этой величины в какой-нибудь момент времени t определяется значением величины tot, стоящей под знаком функции sin в формуле (151.2). Если начальный момент отсчета времени выбран уже так, чтобы мгновенное значение тока проходило через нуль в моменты /=0, Т/2, Т, . . ., то, вообще говоря, другой ток будет проходить через нуль в моменты t=t', t'+Tl2, t'+T, . , и закон его изменения со временем будет иметь вид

t = I _msin<o(t— t') = I_m sin (at—q>), (153.2)

где буквой ф обозначено произведение tot'. Фазой тока (или напряжения) в общем случае называют значение величины, стоящей под знаком функ­ции sin в формуле (153.2), а величина tp=tat'=2nf /Т определяет раз­ность фаз сравниваемых токов (или напряжений). Если эта величина положительна, то первый ток опережает по фазе второй ток, а если она отрицательна, то первый ток отстает по фазе от второго. Фаза измеряется в радианах.