1. Конденсатор емкости 0,001 мкФ заряжен до разности потен-

• циалов 1 кВ. Какой заряд находится на каждой из его пластин?

Простой опыт показывает, что емкость конденсатора за­висит от формы, размеров и взаимного расположения сос­тавляющих его тел; в частности, емкость плоского конден­сатора .зависит от расстояния между его пластинами и от их площади. Зарядим снова при помощи индукции или с помощью электрической машины плоский конденсатор, изображенный на рис. 58, а затем, отсоединив его от маши­ны, станем изменять расстояние между пластинами, раздви­гая и сдвигая их. Если пластины достаточно хорошо изоли­рованы от окружающих тел, то имеющийся на них заряд, очевидно, не может измениться. Однако соединенный с пластинами электрометр показывает, что разность потен­циалов между пластинами не будет оставаться неизменной. Если мы раздвинем пластины, то электрометр покажет, что разность потенциалов между пластинами возросла. Согласно формуле (33.1), это означает, что емкость конден­сатора уменьшилась. Восстановив прежнее расстояние между пластинами, мы вновь получим прежнее показание электрометра и, следовательно, прежнее значение емкости. Уменьшив расстояние между пластинами, мы убедимся, что разность потенциалов между пластинами уменьшилась, т. е. емкость конденсатора увеличилась. Вместо того чтобы отдалять пластины друг от друга, мы можем сдвинуть одну из них в сторону, уменьшив этим- площадь пластин, распо­ложенных друг против друга. Мы увидим, что при этом электрометр тоже показывает увеличение разности потен­циалов, т. е. уменьшение емкости.

Описанные опыты ясно показывают, .что емкость ха­рактеризует не отдельную пластину, а, систему обеих пластин в их взаимном расположении по отношению друг к другу. Поэтому, говоря об электрической емкости, мы всег­да имеем в виду емкость системы из двух тел, между кото­рыми установилась разность потенциалов. Понятно, что это связано с тем обстоятельством (§ 21), что физический смысл имеет только разность потенциалов между двумя точками (в частности, между двумя проводниками; в нашем случае между двумя пластинами, составляющими плоский конденсатор).

Электрометр также представляет собой конденсатор; одним из проводников его является стержень с листками, а вторым — корпус. Емкость электрометра зависит от раз­меров и взаимного расположения его частей. Так как в элек­трометре эти части закреплены в неизменном положении, то емкость данного электрометра будет вполне определен­ной (небольшим изменением емкости, связанным с переме-

щением листков, можно пренебречь, если листки доста­точно удалены от корпуса). Именно поэтому мы и можем пользоваться электрометром для измерения имеющегося па -нем заряда (§ 25). Расхождение листков электрометра определяется полем между ними и корпусом прибора, т. е. разностью потенциалов U между этими телами. Но, соглас­но формуле (33.1), заряд электрометра q равен CU, где С — емкость электрометра, являющаяся для данного прибора постоянной.

Таким образом, по расхождению листков можно судить и о заряде электрометра. Мы можем проградуировать при­бор либо в единицах разности потенциалов (вольтах), либо в единицах заряда (кулонах).

В случае электроскопа, у которого нет металлического корпуса, стержень и листки являются одним проводни­ком, а вторым служат стены и другие окружающие пред­меты, в частности тело экспериментатора, сообщающееся с поверхностью Земли. Заряд, помещенный на электро­скопе, определяет разность потенциалов между стержнем электроскопа и этими окружающими телами. Разделив заряд на эту разность потенциалов, получим емкость кон­денсатора, составленного стержнем электроскопа и окружа­ющими телами, или, как иногда говорят, емкость электро­скопа по отношению к окружающим телам. Но емкость эта уже не будет постоянной, как в случае электрометра, а будет зависеть от случайного расположения окружающих электроскоп тел. Меняя их положение по отношению к электроскопу (например, экспериментатор может прибли­жаться или удаляться от электроскопа), мы будем менять емкость системы, что проявится в изменении показания электроскопа (§ 26).

Конечно, то же самое относится к любому телу: емкость его по отношению к окружающим телам, в частности по отношению к Земле и соединенным с нею стенам помеще­ния и предметам, зависит от расположения тела по отно­шению к этим предметам и, вообще говоря, меняется при перемещении тела. Но если окружающие предметы доста­точно удалены, то небольшие изменения расстояния от данного тела до этих предметов практически не изменяют его емкости. В таком случае тело можно назвать уединен­ным. Электрическую емкость системы (конденсатора), сос­тоящей из уединенного тела и других достаточно удален­ных предметов, часто для краткости речи называют просто электрической емкостью уединенного тела. Она зависит только от формы и размеров данного тела. В част­ности, емкость уединенного шара зависит только от его ра­диуса R и, как показывают расчеты и измерения, выража­ется формулой

C = 4m₀R = ^_mR = i;n-lO'¹⁰R. (33.3)

Шар радиуса 1 см обладает емкостью C=l,ll •10~¹² Ф = = 1,11 пФ.

В том случае, когда мы имеем несколько заряженных тел, изоли­рованных друг от друга, вопрос о емкости становится гораздо сложнее и для определения ее недостаточно простой формулы (33.1). Мы не будем рассматривать этот вопрос. Практически почти всегда приходится иметь дело с двумя проводниками, расположенными очень близ ко друг к другу, и поэтому на их взаимную емкость не влияет расположение других более удаленных проводников.

Если бы Земля представляла собой уединенный проводник, то, так как ее можно считать шаром радиуса 6400 км, ее электрическая ем­кость равнялась бы приблизительно 700 мкФ. Однако, как мы видели в § 29; электрическое поле Земли показывает, что вблизи поверхности Земли, на расстоянии 100—200 км от нее (в ионосфере), расположены электрические заряды, которые совместно с Землей образуют конден­сатор, емкость которого раз в 30—50 больше указанного значения и до­стигает 20 000—30 000 мкФ, т. е. нескольких сотых фарада.

л 33.2. Как измерить разность потенциалов двух проводников, на-

• пример двух изолированных заряженных металлических шаров? Укажите необходимый для этого прибор и начертите схему этих измерений.

3. Почему не убивает током птицу, садящуюся на один из про­водов высокого напряжения? Птицу и поверхность Земли рас­сматривайте как. обкладки конденсатора очень малой емкости (малая поверхность птицы, большое расстояние до Земли).

§ 34. Различные типы конденсаторов. Мы видели в предыду­щем параграфе, что, заряжая любой изолированный про­водник, мы одновременно создаем противоположный заряд на окружающих проводниках, соединенных с Землей и образующих вместе с этим телом конденсатор. Однако ем­кость такого конденсатора мала. Чтобы получить большую емкость, необходимо взять проводники в виде металличе­ских пластин, возможно близко расположенных друг к другу (так называемые обкладки конденсатора). Мы видел», что емкость плоского конденсатора прямо пропорциональна площади обкладок и обратно пропорциональна расстоянию между ними. Поэтому при большой поверхности обкладок и при тонком слое диэлектрика между ними емкость кон­денсатора очень велика, и на нем можно накопить («сгус­тить») значительные заряды даже при небольшом напряже­нии. Отсюда происходит и название «конденсатор» (от ла­тинского слова condensare — сгущать).

На рис; 59, а изображен самый старинный тип конден­сатора — лейденская банка. Это название связано с городом Лейденом (Голландия), где впервые был создан в середине XVIII века конденсатор такого типа. Он представляет со­бой стеклянную банку, оклеенную внутри и снаружи ста­ниолем ¹). Соединение с внут­ренней обкладкой осущест­вляется металлическим стерж­нем, укрепленным внутри бан­ки (рис. 59, б). Для того что­бы зарядить лейденскую бан­ку, ее держат в руке за внеш­нюю обкладку (этим осуще­ствляется соединение с Зем­лей) и прикасаются стержнем к какому-либо заряженному телу, лучше всего к одному из полюсов электрической ма­шины. Емкость лейденской банки средних размеров сос­тавляет около 1000 пФ.

о

>5

6)

Рис. 59. Лейденская банка: а) об­щий вид; б) схема устройства, 1 и 2 — станиолевые обкладки, 3 — стеклянный стакан, 4 — ме­таллический стержень, 5 — уп­ругие металлические полоски для контакта

в% 34.1. Для зарядки лейденской « банки обычно соединяют ее внешнюю обкладку с Землей (держат банку в руках) и ка­саются ее внутренней об­кладкой (стержнем) одного из полюсов электрической машины. Можно ли так же сильно зарядить банку, если, на­оборот, держать в руке ее стержень, а коснуться полюса машины внешней обкладкой? Что произойдет, если заряженную таким образом банку поставить на стол?-

2. Можно ли зарядить лейденскую банку, соединяя одну из ее обкладок с полюсом электрической машины, но оставив вторую обкладку изолированной от Земли?

3. Соединив внешнюю обкладку заряженной лейденской банки с Землей и коснувшись пальцем ее внутренней обкладки, мы чув­ствуем сильный электрический удар. Почему этого не происходит, если мы коснемся внутренней обкладки, стоя на изолирующей скамейке? Человеческое тело на изолирующей скамейке и поверх­ность Земли рассматривайте как обкладки конденсатора, присое­диняемого параллельно банке; учтите, что емкость этого конден­сатора значительно меньше емкости банки.

Для увеличения емкости конденсаторы соединяют в ба­тареи. На рис. 60 изображена батарея из четырех лейден­ских банок. Все внешние и все внутренние обкладки сое-

Рис. 60. Батарея из четырех лейденских банок: / — стержень для зарядки внутренних обкла­док, 2 — стержень для •зазем­ления внешних обкладок

Рис. 61. Конденсатор перемен­ной емкости состоит из двух изолированных систем металли­ческих пластин 1 и 2, которые входят друг в др^га при вра- . щении рукоятки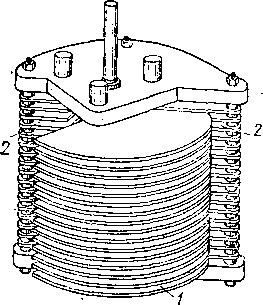

динены между собой, и поэтому батарею можно рассматри­вать как один большой конденсатор, у которого площадь обкладок равна сумме площадей обкладок отдельных ба­нок. Емкость батареи при таком соединении (оно называет­ся параллельным соединением) равна сумме емкостей от­дельных конденсаторов.

На рис. 61 показан конденсатор переменной емкости, широко употребляющийся в радиотехнике. Он состоит из двух изолированных систем металлических пластин, кото­рые входят друг в друга при вращении рукоятки. Вдвига­ние и выдвигание одной системы пластин в другую изменя­ют емкость конденсатора (§ 33).

Большинство технических конденсаторов приближается по типу к плоскому конденсатору, т. е. в основе своей представляет две разделенные небольшим зазором парал­лельные плоские поверхности (обкладки), на которых сосре­доточены равные заряды противоположных знаков. Элек­трическая емкость плоского конденсатора сравнительно просто выражается через размеры его частей. Выполним опыт, изображенный на рис. 58, причем будем применять приборы, проградуированные так, что они позволят изме­рять и заряд, сообщаемый конденсатору, и возникающую

разность потенциалов. Изменяя площадь S пластин и рас­стояние между "йими d, мы убедимся в том, что емкость плоского конденсатора

^{C = e}o~d ^ 4я-9-10* ~d ‘ (^34-1)

К формуле (34.1) можно было прийти и путем теорети­ческих расчетов. Как при измерениях, так и при расчетах предполагается, что конденсатор плоский, т. е. что расстоя­ние d очень мало по сравнению с линейными размерами пластин, и в зазоре между пластинами находится воздух (точнее следовало бы предполагать, что и воздух отсутст­вует).

В_соответствии с формулой (34.1)

С(Ф]й[м]

^е°⁼ sm »

откуда следует, что е₀ может быть выражена в фарадах на метр (Ф/м) (§11).

HI—iHHh

C_i C_z

К источнику заояс/а 6)

§ 35. Параллельное и последовательное соединение конден­саторов. Помимо-показанного на рис. 60 и 61, а также на рис. 62, а параллельного соединения конденсаторов, при котором соединены между собой все положительные и все отрицательные обкладки, иногда соединяют конденсаторы последовательно, т. е. так, чтобы отрицательная обкладка

		L1
	сг	% -	•ft* о

И источники . -варяda

а)

Рис. 62. Соединение конденсаторов: а) параллельное; б) последова­тельное

первого конденсатора была соединена с положительной обкладкой второго, отрицательная обкладка второго — с положительной обкладкой третьего и т. д. (рис. 62, б).

В случае параллельного соединения все конденсаторы заряжаются до одной и той же разности потенциалов U, но заряды на них могут быть различными. Если емкости их равны С_и С₂, . . ., С_п, то соответствующие заряды будут

q₁a=C₁U, q₂z=C₂U, .q_n — C_nU,

Я *= <7i + <7₂ + • • •' + <7л — (Ci + С₂ + • • • + С_п) U,

и, следовательно, емкость всей системы конденсаторов

(35.1)

С — jf — C_t -f- С₂ + ... + С_П.

Итак, емкость группы параллельно соединенных конден­саторов равна сумме емкостей отдельных конденсаторов.

В случае последовательно соединенных конденсаторов (рис. 62, б) одинаковы заряды на всех конденсаторах. Дей­ствительно, если мы поместим, например, заряд +q на ле­вую обкладку первого конденсатора, то вследствие индук­ции на правой его обкладке возникнет заряд —q, а на левой обкладке второго конденсатора — заряд +<7 *)• Наличие этого заряда на левой обкладке второго конденсатора опять- таки вследствие индукции создает на правой его обкладке заряд —<7, а на левой обкладке третьего конденсатора — заряд +q и т. д. Таким образом, заряд каждого из последо­вательно соединенных конденсаторов равен q. Напряжение же на каждом из этих конденсаторов определяется ем­костью, соответствующего конденсатора:

где С; — емкость одного конденсатора. Суммарное напря­жение между крайними (свободными) обкладками всей группы конденсаторов

Следовательно, емкость всей системы конденсаторов

определяется выражением

*) Конечно, наше рассуждение остается правильным для конден­саторов всех видов, как плоских, так и не плоских. В любом конденса- торе все поле сосредоточено между его обкладками (например, между двумя обкладками цилиндрического конденсатора). Поэтому заряд, ин­дуцированный на второй обкладке, всегда равен по модулю и противо­положен по внаку заряду, помещенному на первую обкладку.

(35.2)

Из этой формулы видно, что емкость группы последователь­но соединенных конденсаторов всегда меньше емкости каж­дого из этих конденсаторов в отдельности.

^ 35-1. Четыре одинаковых конденсатора соединены в одном случае

• параллельно, в другом — последовательно. В каком случае ем­кость этой группы конденсаторов больше и во сколько раз?

2. Два конденсатора емкости 2 и 1 мкФ соединены последова­тельно и присоединены к полюсам батареи с напряжением 120 В. Каково напряжение между обкладками первого и между обклад­ками второго конденсатора?

3. Какой заряд нужно сообщить батарее из двух лейденских банок емкости 0,0005 и 0,001 мкФ, соединенных параллельно, что­бы зарядить ее до напряжения 10 кВ?

4. Конденсатор, заряженный до напряжения 100 В, соединя­ется с конденсатором такой же емкости, но заряженным до 200 В, параллельно (т. е. положительная обкладка — с положительной, отрицательная — с отрицательной). Какое установится напряже­ние между обкладками?

5. Два заряженных металлических шара одинакового диаметра приводятся в соприкосновение. Один из шаров — полый. Поров­ну ли распределятся заряды на обоих шарах?

§ 36. Диэлектрическая проницаемость. Емкость конденса­тора зависит, как показывает опыт, не только от размера, формы и взаимного расположения составляющих его про­водников, но также и от свойств диэлектрика, заполняю­щего пространство между этими проводниками. Влияние

I I I Г

Рис. 63. Емкость конденсатора увеличивается при вдвигании эбони­товой пластинки между его обкладками. Листки электрометра спадают, хотя заряд остается прежним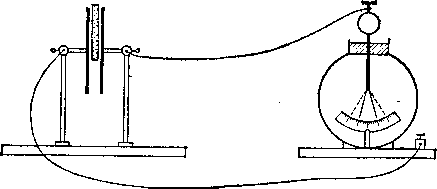

диэлектрика можно установить при помощи следующего опыта. Зарядим плоский конденсатор и заметим показа­ния электрометра, измеряющего напряжение на конденса­торе. Вдвинем затем в конденсатор незаряженную эбони­товую пластинку (рис. 63). Мы увидим, что разность потенциалов между обкладками заметно уменьшится. Если удалить эбонит, то показания электрометра делаются прежними. Это показывает, что при замене воздуха эбони­том емкость конденсатора увеличивается. Взяв вместо эбо­нита какой-нибудь иной диэлектрик, мы получим сходный результат, но только изменение емкости конденсатора будет иным. Если С₀ — емкость конденсатора, между обкладками которого находится вакуум, а С — емкость того же конден­сатора, когда все пространство между обкладками запол­нено, без воздушных зазоров, каким-либо диэлектриком, то емкость С окажется в е раз больше емкости С₀, где е за­висит лишь от природы диэлектрика. Таким образом, мож­но написать

С — (36.1)

Величина е называется относительной диэлектричес­кой проницаемостью или просто диэлектрической прони­цаемостью среды, которой заполнено пространство между обкладками конденсатора ¹). В табл. 1 приведены значения диэлектрической проницаемости некоторых веществ.

Таблица 1. Диэлектрическая проницаемость некоторых веществ

Вещество	е
Вода (чистая)	81
Воздух	1,0006
Кварц	4,5
Керамика (радиотехническая)	до 80
Парафин	2,3
Слюда	6—8
Стекло	4—7
Эбонит.	3
Янтарь	2,8

Сказанное справедливо не только для плоского конден­сатора, но и для конденсатора любой формы: заменяя воз­дух каким-либо диэлектриком, мы увеличиваем емкость конденсатора в е раз.

Строго говоря, емкость конденсатора увеличивается в е раз только в том случае, если все линии поля, идущие от одной обкладки к другой, проходят в данном диэлектрике. Это будет, например, у конденсатора, который целиком погружен в какой-либо жидкий диэлектрик, налитый в большой сосуд. Однако если расстояние между обкладками мало по сравнению с их размерами, то можно считать, что достаточно заполнить только пространство между обкладками, так как именно здесь практи­чески сосредоточено электрическое поле конденсатора. Так, для плоского конденсатора достаточно заполнить диэлектриком лишь пространство между пластинами.

Помещая между обкладками вещество с большой диэлек­трической проницаемостью, можно сильно увеличить ем­кость конденсатора. Этим пользуются на практике, и обычно в качестве диэлектри­ка для конденсатора выбира­ют не воздух, а стекло, пара­фин, слюду и другие вещест­ва. На рис. 64 показан техни­ческий конденсатор, у которо­го диэлектриком служит про­питанная парафином бумаж­ная лента. Его обкладками являются станиолевые ¹) лис­ты, прижатые, с обеих сторон к парафинированной бумаге.

Рис. 64. Технический плоский конденсатор: а) в собранном ви­де; б) в частично разобранном виде: 1 ц Г — станиолевые лен­ты, между которыми проложе­ны ленты парафинированной тонкой бумаги 2. Все ленты вместе складываются «гармош­кой» и вкладываются в метал­лическую коробку. К концам лент 1 и Г припаиваются кон­такты 3 и 3' для включения кон­денсатора в схему

свойствами. В противном ' случае заряды будут утекать через диэлектрик. Поэтому вода, несмотря на ее большую диэлектрическую прони­цаемость, совсем не годится для изготовления конденсато­ров, ибо только исключительно тщательно очищенная во­да является достаточно хорошим диэлектриком.

Емкость таких конденсато­ров нередко достигает нес­кольких микрофарад. Так, например, радиолюбительский конденсатор размером со спи­чечную коробку имеет емкость

2. мкФ.

Понятно, что для изготов­ления конденсатора пригодны только диэлектрики с очень хорошими изолирующими

Если пространство между обкладками плоского конден­сатора заполнено средой с диэлектрической проницаемостью е, то формула (34.1) для плоского конденсатора принимает вид

С = 88₀4-. (36.2)

То обстоятельство, что емкость конденсатора зависит от окружающей среды, указывает, что электрическое поле внутри диэлектриков изменяется. Мы видели, что при за­полнении конденсатора диэлектриком с диэлектрической проницаемостью е емкость увеличивается в е раз. Это зна­чит, что при тех же самых зарядах на обкладках разность потенциалов между ними уменьшается в 8 раз. Но разность потенциалов и напряженность поля связаны между собой соотношением (30.1). Поэтому уменьшение разности потен­циалов означает, что напряженность тля в конденсаторе при его заполнении диэлектриком делается меньше в е раз. В этом и состоит причина увеличения емкости конденсатора.

Если обозначить через Е₀ напряженность поля, создан­ного любыми заряженными телами в некоторой точке в вакууме, а через Е напряженность поля в этой же точке в том случае, когда при тех же зарядах все пространство заполнено диэлектриком с диэлектрической проницаемостью е, то

£=4°. (36.3)

Если два точечных заряда находятся в диэлектрике, то напряженность поля каждого из зарядов в точке, где на­ходится другой заряд, уменьшается также в е раз и, следо­вательно, сила, действующая на каждый из зарядов, в г раз меньше, чем в вакууме. Отсюда заключаем, что закон Кулона (10.1) для точечных зарядов, помещенных в 'ди­электрике, имеет вид ¹)

(³⁶-⁴)

§ 37. Почему электрическое поле ослабляется внутри диэлектрика? Поляризация диэлектрика. Чтобы понять, почему поле внутри диэлек­трика меньше, чем в вакууме, нужно учесть, что все тела построены из атомов и молекул. Атомы и молекулы в свою очередь состоят из поло­жительных и отрицательных зарядов (атомных ядер и электронов), так что всякий-диэлектрик представляет собой собрание большого числа за­ряженных частиц.

В молекулах эти положительные и отрицательные заряды нередко расположены так, что одна половина молекулы имеет по преимуществу положительный заряд, а другая — отрицательный. Такая молекула, грубо говоря, имеет вид палочки или стрелки с противоположно заряжен­ными концами (рис. 65). Такие молекулы часто называют диполями (двухполюсниками, от греческого слова «ди» — два). Положительный и отрицательный заряды в каждой молекуле одинаковы, и поэтому лю­бая молекула в целом не заряжена.

(*+***

Рис. 65. Модель дипольной мо­лекулы диэлектрика

Однако при помещении дипольных молекул в электрическое поле на каждую молекулу будут действо­вать силы, стремящиеся установить ее по направлению линий поля.

В естественном состоянии, т. е. в отсутствие внешнего поля, моле­кулы вещества ориентированы совершенно хаотически. В любой части диэлектрика будут находиться одинаковые положительные и отрицатель­ные заряды в самом хаотическом расположении (рис. 66, а), и поэтому результирующее действие этих зарядов будет равно нулю. Когда мы помещаем диэлектрик с дипольными молекулами в электрическое поле,

Рис. 66. Поляризация диэлек­трика в электрическом поле: а) электрическое поле отсутству­ет; б) электрическое поле сла­бое; в) электрическое поле силь­ное. Условно положительно за­ряженный конец диполя обоз­начен штриховкой

Ф

б)

в)

	•;+.
•X-V.feV.

ч

Рис. 67. Поле Е_р, создан­ное поляризационными за­рядами -\-q' и —q', нап­равлено противоположно полю Ео, которое созда­но зарядами -\-q и —q на обкладках конденсатора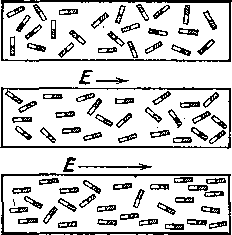

то под действием сил поля, стремящихся повернуть диполи, молекулы поворачиваются так, чтобы их электрические оси установились по воз­можности по линиям поля. Говоря «по возможности», мы имеем в виду следующее. Действие электрического поля стремится установить упо­рядоченное расположение молекул, выстроить их цепочками, как пока­зано на рис. 66, б и в.

С другой стороны, тепловое движение молекул (см. том I) стремится все время расстроить эту упорядоченность и восстановить хаотическое, беспорядочное расположение молекул, показанное на рис. 66, а. Борьба между этими противоположно направленными факторами, из которых первый зависит от напряженности поля и индивидуальных свойств дан­ного вещества, а второй определяется температурой, приводит к тому,

что в поле данной напряженности не все, а лишь большая или меньшая часть молекул располагается своими осями близко к направлению поля.

Следствием этого упорядочения в расположении молекул является то, что на поверхности диэлектрика образуются равные по модулю, но противоположные по знаку электрические заряды. Эти заряды тем- больше, чем более упорядочено расположение молекул. На рис. 66, е заряд на границах диэлектрика больше, чем на рис. 66, б. Диэлектрик приобретает «электрические полюсы» или, как принято говорить, поля­ризуется. Причина ослабления поля в диэлектрике и заключается в по­ляризации последнего;

Действительно, представим себе плоский конденсатор, заполненный диэлектриком (рис. 67), причем на левой обкладке имеется положитель­ный заряд, а на правой — отрицательный. Так как одноименные заряды отталкиваются, а разноименные притягиваются, то, очевидно, у левой (положительной) обкладки возникает на поверхности диэлектрика от­рицательный поляризационный заряд, а у правой обкладки — положи­тельный. Таким образом, поле Е_р, создаваемое поляризационными за­рядами, направлено противоположно полю Е₀, создаваемому зарядами на обкладках, и потому ослабляет его. Результирующее поле в диэлек­трике оказывается меньше, чем в отсутствие диэлектрика.

Мы рассматривали до сих пор только действие поля на диэлектрик, проявляющееся в повороте молекул и упорядочении их ориентации. Кроме этого действия поля, в некоторых веществах возможно и смеще­ние зарядов в пределах каждой молекулы или, как говорят, поляри­зация каждой отдельной молекулы. Это действие поля еще более увеличивает поляризационные заряды,.возникающие на поверхности диэлектрика, и, следовательно, приводит к еще большему ослаблению результирующего поля.

ЕЗЕЗЕЗЕЗЕЗЕЗЕЗЕЗ ЕЗ ЕЗ ЕЭ ЕЗ ЕЗ ЕЗ 513 ЕЯ ЕЭЕЗОЕЗЕЗЕЗЕЗЕЗ

а)

4- +

+

ОЕЭЕЭЕЗ	—	+	ЕЭЕЭЕЗЕЗ	•41
ОЕЭЕЭЕЭ	-	+	ЕЗ E3GE3E3	—
E3E3EI3E3	-	+	ЕЗЕЗЕЗЕЗ	—

Рис. 68. При разделении поляризованного диэлектрика на две части на поверхности каждой из них возникают поляризационные заряды противоположных знаков. Поляризация диэлектрика: о) до разделе­ния; б) после разделения

Поляризация диэлектриков напоминает собой элйстризацию через влияние (§8). Однако между этими явлениями существует и различие. Мы видели, что электризация проводников посредством влияния объяс­няется перемещением свободных электронов, которые в * проводниках могут передвигаться по всему объему проводника. Разъединяя в элек­трическом поле проводник на две части, мы можем отделить индуциро­ванные заряды, и обе половины проводника останутся заряженными даже после устранения поля, вызвавшего эти заряды. В противоположность этому, внутри диэлектрика электрические заряды не могут свободно перемещаться, а могут .только смещаться в пределах своей молекулы.

Поэтому, если разделить поляризованный диэлектрик в электрическом поле на две части, то каждая часть будет состоять по-прежнему из неза­ряженных в целом молекул, и полный ее заряд тоже будет равен нулю. На поверхности каждой из частей заряды, однако, будут, и притом на одном конце положительные? а на другом — отрицательные (рис. 68). Это и понятно, так как к каждой части можно применить те же рассуж- ' дения, что и для целого куска диэлектрика. При устранении внешнего поля заряды внутри молекул под действием теплового движения возвра­щаются в исходное неупорядоченное расположение, и поляризацион­ные заряды исчезают. Мы видим, что поляризационные заряды, в отли­чие от индуцированных, не могут быть отделены друг от друга. Поэтому поляризационные заряды часто называются еще связанными зарядами.